
Biomehanika sa kineziologijom (praktikum) Pregled
1
1. PROPORCIJE GRAĐE ČOVJEČIJEG TIJELA
- KANON
(zadatak br. 1)
Na stranicama ovog praktikuma biće više riječi o porijeklu i postupku grafičkog
prikazivanja aparata za kretanje čovjeka usvojenog na Fakultetu sportskih nauka
Univerziteta u Banja Luci. Međutim, o historijskom razvoju i značaju
proučavanja proporcije građe čovječijeg tijela, opširnije je dato u udžbeniku „
Biomehanika sportske lokomocije“ od prof. dr Branimira Mikića i prof. dr Gruje
Bjekovića.
Usvojeno pravilo crtanja građe čovječijeg tijela i
zvršeno je prema kanonima više
autora, sa izvjesnim zaokruživanjem izvršenim na predmetu „Biomehanika“
Fakulteta sportskih nauka u Banja Luci. U najvećoj mjeri primjenjeno je pravilo
crtanja građe čovječijeg tijela prema Karl Schmidtu razrađeno i upotpunje
no od
Gustava Fritscha. Za modul je uzeta visina kićmenog stuba (rastojanje između
centra potiljačnog zgloba i sredine ose koja spaja centre zglobova kukova), čija
projekcija na prednju stranu tijela u normalnom uspravnom stavu obuhvata
prostor od donjeg r
uba nosne pregrade do gornje ivice simfizne glačice. Osnovni
modul je podijeljen na četiri jednaka dijela
-
submodula, a visina čovjeka iznosi
10,5 submodula.
Usvojeno pravilo crtanja građe čovječijeg tijela u frontalnoj i sagitalnoj ravni, za
srednji konstitucionalni tip, u normalnom uspravnom stavu dato je prema ovim
autorima:
FRONTALNA RAVAN:
•
proporcije glave su prema KARL SCHMIDTU šematizovane na prikladan
način od STRATZA,
•
proporcije trupa, gornjih i donjih ekstremiteta su prema K. SCHMIDTU,
odnosno G. FRITSCHU.
SAGITALNA RAVAN:
•
proporcije konture glave su prema K. SCHMIDTU,
•
krivine kičmenog stuba konstruisane su lukovima zaokruživanjem
parametara više autora,
•
karlična osa je prema R. FICKU, a stopalo prema J. KOLLMANU.
Za izradu zadatka br. 1 potrebno
je od pribora imati: olovku srednje i veće
tvrdoće, trougao srednje veličine od 30 i 45 stepeni i šestar.
Od kandidata se traži da zadatak izvrši tačno, uredno i da isti završi u
predviđenom roku.
2
Skica aparata za kretanje u obje ravni crta se prvo pomoćni
m linijama debljine
od 0,1 -
0,3 mm, a zatim se ucrtavaju biomehaničke poluge linijama debljine 0,4
- 0,8 mm.
Ispitni zadatak se ne označava brojevima i slovima, kao što je to učinjeno u
praktikumu na slici 2 i 3.
Za primjer
„kanona
“ u praktikumu uzeta je razmjera za crtanje (1
SUBMODUL: 24 mm
.).
1.1. Proporcije građe čovječijeg tijela u frontalnoj ravni
Na listu papira formata A4 izvuče se pomoćnim linijama 12 horizontalnih linija
preko cijelog lista papira po širini i dvije vertikalne linije od prve do dvanaeste
horizontalne linije po visini (slika 1).
Prva horizontalna linija udaljena je od gornje ivice lista 26 mm i odgovara
početku prvog submodula. Preostalih jedanaest horizontalnih linija ucrtava se na
međusobnom rastojanju od 24 mm (1 submodul), osi
m zadnje linije koja se
nalazi na rastojanju od ½ submodula. Odnosno, rastojanje od prve horizontalne
linije do zadnje (dvanaeste) iznosi 252 mm, tj. 10,5 submodula.
Vertikalne linije A - A i B - B dijele list papira na tri jednaka dijela po visini, na
kojima se skica aparata za kretanje crta u frontalnoj i sagitalnoj ravni.
Radi bolje orijentacije pri crtanju skica aparata za kretanje, međuprostori između
horizontalnih linija tj. submoduli su obilježeni rimskim brojevima od I - XI i
upisani pored desne stranice lista papira. Prva horizontalna linija odgovara
početku prvog submodula. Druga horizontalna odgovara bazi prvog i početku
drugog submodula, treća bazi drugog i početku trećeg submodula itd. do
dvanaeste horizontalne linije, koja predstavlja samo bazu jedanaestog
submodula (½). Odnosno, gornja horizontalna linija svakog submodula
odgovara početku submodula, a donja njegovoj bazi.
Prema usvojenom kanonu skica aparata za kretanje u frontalnoj ravni za
normalni uspravni stav crta se ovim redom:
1.1.1
Karlična osa
-
udaljenost karlične ose od najviše tačke glave (početak 1
sbm) izn
osi 5 sbm i poklapa se sa gornjim rubom simfizne glačice (baza 5 sbm).
Rastojanje između centra zglobova kukova tj. veličina karlične ose iznosi 1 sbm.
Rastojanje centra zglobova kukova od središnje ose tijela A - A je ½ sbm.
4
5
1.1.2 Ramenska osa -
rastojanje između ramenske i karlične ose iznosi 3 sbm i
nalazi se u nivou sredine drške grudne kosti. Rastojanje iznosi između centra
zglobova ramena 2 sbm, odnosno po 1 sbm od središnje ose tijela A - A na bazi
drugog submodula. Centri zglobova obilježe
ni su tačkama.U daljem postupku
crtanja po kanonu, nanose se dvije dijagonalne linije koje povezuju centar
zgloba ramena jedne strane tijela sa centrom zgloba kuka druge strane ili prema
usvojenom načinu spojiti tačku 3 sa tačkom 2 i tačku 4 sa tačkom 1. D
ijagonale
se ukrštaju u tačci presjeka baze IV submodula i središnje ose tijela A
- A, što
odgovara mjestu gdje se nalazi središte pupčanog otvora O.
1.1.2
Glava
-
ključ proporcije glave u frontalnoj ravni određen je pomoću dva
kruga poluprečnika R = ½ sbm i r
= 1/3 sbm. Centar većeg kruga se nalazi na
središnjoj osi tijela A - A na sredini prvog submodula, a centar manjeg kruga na
bazi prvog submodula N (baza nosa, odnosno nivo donjeg ruba nosne pregrade).
U daljem postupku konstrukcije glave veći krug se prep
olovi horizontalnom
linijom 5 - 6. Zatim se ucrtaju prave linije od centara zglobova ramena 3 i 4
preko baze nosa N do mjesta gdje horizontalna linija 5 -
6 polovi obim većeg
kruga. Odnosno, izvuku se linije od tačke 3
- 6 i 4 -
5. Dalje se tačke 5 i 6
pov
ezuju sa tačkom presjeka početka prvog submodula i ose A
- A. Dijagonale
ucrtanog kvadrata podudaraju se sa osama koordinatnog sistema. Bočne strane
obrisa glave predstavljaju se dvjema tangentama na oba kruga T i T1.
1.1.4
Položaj prsne bradavice
- od središnje ose tijela A - A sa baze drugog
submodula 7 izvuku se prave linije prema dijagonalama 3 - 2 i 4 - 1 (centar
zgloba ramena - centar zgloba kuka) tako, da budu paralelne sa linijama 3 - N -
6 i 4 - N - 5 (centar zgloba ramena, baza nosa do obima velikog kruga). Presjek
ucrtanih linija sa dijagonalama određuje položaj središta prsnih bradavica P i P1.
Rastojanje između prsnih bradavica odgovara visini glave (od najviše tačke
glave do vrha brade).
1.1.5 Gornji ekstremiteti
- iz centra zglobova ramena 3 i 4, izvuku se vertikalne
linije do baze VII sbm, na kojima se konstruišu proporcije nadlakta, podlakta i
šake.
1.1.5.1 Dužina nadlaktice
-
odgovara rastojanju između centra zgloba ramena
prsne bradavice sa suprotne strane 3 - P1 ili 4 - P. Šiljak šestara se postavi u
centar desnog zgloba ramena 3 i opiše luk od prsne bradavice sa suprotne strane
P1 do vertikalne linije izvučene iz tačke 3. Tačka presjeka pomenutog luka i
vertikale odgovara mjestu centra zgloba lakta 8. Centar zgloba lakta lijeve ruke
9 prenosi se na vertikalu projekcijom centra zgloba lakta desne ruke.
1.1.5.2 Dužina podlaktice
-
jednaka je razdaljini između prsne bradavice i
pupčanog otvora P
- O ili P1 - O. Za razliku od položaja centra zgloba lakta,
centar zgloba korijena šake nalazi se upolje od vertikalne linije spuštene iz

7
1.2
Proporcije građe čovječijeg tijela u sagitalnoj ravni
Skica aparata za kretanje čovjeka crta se prema kanonu u sagitalnoj ravni
posmatrana sa desne strane tijela, tako da je skica aparata okrenuta licem prema
desnoj stranici lista papira što odgovara pravilu projekcije usvojene u našoj
zemlji.
Prema kanonu, skica aparata za kretanje čovjeka u sagitalnoj ravni za normalni
uspravni stav crta se ovim redom (slika 2 i 3).
1.2.1 Donji ekstremiteti
- dužina stopala iznosi 1,5 sbm i nanosi se od vertikalne
linije B - B (u daljem tekstu osnovna vertikala) u lijevu i desnu stranu po ½
cijele dužine stopala na bazu XI sbm. Dobijene tačke 20 i 21 odgovaraju mjestu
ek
stremnih tačaka pete i prstiju. Centar skočnog zgloba se nalazi sa lijeve strane
osnovne vertikale (B -
B) na bazi X sbm na rastojanju od krajnje tačke petne
kosti (20) za ¼ cijele dužine stopala. U našem slučaju za odnos 1 sbm: 24 mm,
rastojanje centra sk
očnog zgloba od ekstremne tačke petne kosti (20) iznosi 9
mm.
U daljem postupku ova se veličina nanosi na bazu XI sbm i podizanjem
vertikalne linije do baze X sbm odredi mjesto centra skočnog zgloba (22).
Ucrtavanjem linije 20 - 22 i 22 - 21 odredi se bio
mehanička poluga za stopalo.
Dužine potkoljenica i natkoljenica određene su u frontalnoj ravni i nanose se
projekcijom na liniju koja spaja centar skočnog zgloba (22) sa centrom zgloba
kuka (23 - na presjeku baze V sbm i osnovne vertikale B - B).
1.2.2 Kar
lični pojas
-
u sagitalnoj ravni predstavljen je linijom koja spaja tačku
na sredini karlične ose (u normalnom uspravnom stavu poklapa se sa centrima
zglobova kukova) sa mjestom spoja karlice i kičmenog stuba.
Ista linija je podudarna sa projekcijom FICKOVE konjugate koja spaja zadnju
gornju bedrenu bodlju (spina iliaca posterior superior) sa preponskom kvržicom
(tuberculum pubicum).
Ugao između FICKOVE konjugate i horizontale za normalan uspravan stav
iznosi 60 stepeni i konstruiše se na sljedeći način:
sa proizvoljnim otvorom
šestara opiše se luk u lijevu stranu od osnovne vertikale (B - B) do baze V sbm
sa centrom luka u centru zgloba kuka (23). Zatim se ista veličina u otvoru
šestara (poluprečnik luka) nanese od baze V sbm na ucrtani luk. Dobijeni
presjek (24) se spaja sa centrom lukatj. Centrom zgloba kuka (23), a ugao pod
kojim naliježe ucrtana osa na horizontalu iznosi 60 stepeni.
Centar spoja karlice i kičmenog stuba (25) nalazi se na pomenutoj osi 23
- 24 na
rastojanju od baze V sbm za ¾ submodula koji se nanosi po osnovnoj vertikali
(B - B).
8
Ucrtavanjem horizontalne linije u lijevu stranu od tačke 26 dobija se presjek 25
koji odgovara mjestu centra spoja kičmenog stuba i karlice.
Zatim se nanosi vertikalna linija B1 -
B1 (u daljem tekstu pomoćna
vertikala) od
početka prvog sbm do baze V sbm, na udaljenosti od osnovne vertikale B
- B u
lijevu stranu sa ¼ sbm. U međuprostoru između osnovne i pomo
ćne vertikale
konstruiše se kičmeni stub u sagitalnoj ravni predstavljen krivom linijom
sadržanom od tri
luka. Međutim, osim nanošenja pomoćne vertikale, crtanje
slabinskog, grudnog i vratnog dijela kičmenog stuba nastavlja se poslije
konstruisanja glave u profilnoj ravni, jer većina parametara za crtanje kičmenog
stuba proizilazi iz konstrukcije profila glave.
1.2.3 Glava
- konstrukcija glave u sagitalnoj ravni spada u najsloženiji dio
crtanja prema kanonu, a time i potreba što preciznijeg mjerenja.
Kao polazna tačka za crtanje glave u profilnoj ravni je krug poluprečnika ½ sbm
sa centrom na sredini prvog s
bm na pomoćnoj vertikali B1
- B1. Tako da linije
početka i baze I sbm predstavljaju tangente kruga. Dodavanjem još dvije bočne i
uspravne tangencijalne linije, isti krug se uokviri kvadratom 28 - 29 - 30 - 31 (u
daljem tekstu manji kvadrat).
Gornja stranica malog kvadrata se produžava u desnu stranu za 1/3 sbm, a lijeva
starnica prema dole za istu veličinu. Dodavanjem donje i desne stranice veličine
1 1/3 sbm formira se kvadrat 28 - 32 - 34 - 32 (u daljem tekstu veliki kvadrat).
U daljem postupku ucrtava s
e luk poluprečnika 1 sbm sa centrom na presjeku
baze prvog submodula i pomoćne vertikale B1
-
B1 (centar potiljačnog zgloba
N1). Sa otvorom šestara od 1 sbm i šiljkom šestara u centru potiljačnog zgloba
N1 opiše se luk od desne strane malog kvadrata (35) do baze prvog sbm (36).
Dobijeni presjek (36) na bazi prvog sbm je centar narednog većeg luka. Veličina
poluprečnika većeg luka odgovara rastojanju od presjeka 36 do presjeka manjeg
luka sa desnom stranicom manjeg kvadrata (35). Šiljak šestara se postavi u
tačku
presjeka (36) i od tačke 35 opiše luk do donje starnice većeg kvadrata (C1).
Veliki luk (35 -
C1) predstavlja obris profila lica, a presjek C1 ekstremnu tačku
donje vilice.
Linija koja odgovara donjoj ivici donje ivice nalazi se na liniji koja spaja
tačku
presjeka velikog luka i donje stranice velikog kvadrata (C1) sa tačkom presjeka
malog luka i baze I sbm, odnosno centrom velikog luka (36). Dužina i položaj
donje vilice odgovara rastojanju od tačke C1 do tačke presjeka osnovne
vertikale (B - B) sa linijom C1 - 36 (ugao donje vilice - 37).Zadnja ivica donje
vilice nanosi se na liniju koja spaja ugao donje vilice (37) sa tačkom na
pomoćnoj vertikali udaljenoj za 1/3 sbm od početka prvog sbm (38).

10
Dužina i položaj zadnje ivice donje vilice odgovara rastojanju od ugla donje
vilice (37) do tačke presjeka linije 37
- 38 i baze I sbm.
1.2.4 Kičmeni stub
–
konstrukcija kičmenog stuba prikazana krivom linijom,
sastavljena je od tri luka koji odgovaraju slabinskoj, grudnoj i vratnoj krivini
kičmenog stuba. Gledano sa leđne strane slabinska i vratna krivina su
konkavnog oblika, a centri njihovih lukova nalaze se sa lijeve strane od osnovne
vertikale B - B. Grudna krivina je konveksnog oblika, a centar luka koji ona
formira nalazi se sa desne strane od osnovne vertikale. Sva tri luka se ucrtavaju
u među prostoru između osnovne i pomoćne vertikale, osim donjeg dijela
slabinske krivine koji izlazi iz pomenutog prostora u dorzalnom smjeru.
Visina slabinskog dijela kičmenog stuba jednaka je 1 sbm i ista se ucrtava u
pravougaonik čije se bočne stranice poklapaju sa pomoćnom i osnovnom
vertikalom.
Donja stranica pravougaonika je granična linija (26) između karlice i slabinskog
dijela kičmenog stuba i udaljena je od baze V sbm za ¾ sbm. Gornja stranica
pravougaonika (3
8) je granična linija između slabinskog i grudnog dijela
kičmenog stuba i udaljena je od granične linije (26) za 1 sbm.
Visina grudnog dijela kičmenog stuba jednaka je 1,5 sbm i ista se ucrtava u
pravougaonik koji je nadovezan na gornju stranicu (38) pravougaonika za
konstruisanje krivine.
Visina vratnog dijela kičmenog stuba jednaka je ¾ sbm i ista se ucrtava u
prostoru, odnosno pravougaoniku koji se nadovezuje na gornju stranicu (39)
pravougaonika za konstrukciju grudnog dijela kičmenog stuba. Gornja stra
nica
pravougaonika za konstrukciju vratne krivine poklapa se sa bazom prvog sbm.
Praktično, prvo se crta grudna, pa slabimska i najzad vratna krivina.
1.2.4.1 Grudna krivina -
konstruisana je lukom čiji je poluprečnik određen
veličinom rastojanja od vrha
donje vilice C1 preko centra kruga (27) do obima
istog kruga C. Udaljenost centra luka od baze V sbm iznosi 2 ½ sbm.
U postupku crtanja luka grudnog dijela kičmenog stuba, prvo se izvuče
horizontalna linija od pomoćne vertikale u desnu stranu do desne str
anice lista
papira, a na rastojanju od baze V sbm za 2,5 sbm. Zatim se u otvor šestara unese
veličina poluprečnika C1
- C i opiše luk sa centrom (40) na ucrtanoj horizontali.
Luk tangira pomoćnu vertikalu B1
- B1 i presjeca gornju i donju stranicu
pravouga
onika predviđenog za konstruisanje grudne krivine kičmenog stuba.
1.2.4.2 Slabinska krivina -
konstruisana je lukom poluprečnika ¾ sbm.
Udaljenost centra luka od baze V sbmodgovara rastojanju tačke presjeka desne
stranice velikog kvadrata (32 - 34) i baze
I sbm (D1) do tačke koja polovi lijevu
stranicu malog kvadrata (D). Za nanošenje luka kojim se predstavlja slabinska
11
krivina kičmenog stuba, izvlači se horizontalna linija u lijevu stranu od osnovne
vertikale B - B dužine 2 sbm na rastojanju od baze V sbm
za veličinu D
- D1.
Na ucrtanoj horizontalnoj liniji postavlja se šiljak šestara i opisuje luk
poluprečnika ¾ sbm koji tangira osnovnu vertikalu i spaja se sa donjim krajem
luka grudne krivine i centrom spoja karlice i slabimske krivine (25).
1.2.4.3 Vratna krivina -
konstruisana je lukom čiji poluprečnik odgovara
rastojanju između tačke presjeka linije zadnje ivice donje vilice (37
- 38) i baze
prvog sbm (E) do tačke E1 koja polovi desnu stranu malog kvadrata (29
- 31).
Udaljenost centra luka od baze I s
bm odgovara rastojanju od tačke presjeka
pomoćne vertikale B1
- B1 i gornje stranice pravougaonika za konstrukciju
grudnog dijela kičmenog stuba 39 (F) do tačke presjeka osnovne vertikale B
- B
i donje strane velikog kvadrata 33 - 34 (F1). Pošto se ucrta horizontalna linija od
osnovne vertikale u lijevu stranu za 1 sbm na udaljenosti od baze prvog sbm za
veličinu F
- F1, ucrta se luk koga tangira osnovna vertikala, spaja se sa gornjim
dijelom luka grudnog dijela kičmenog stuba i završava se u centru potiljačnog
zgloba (N1).
Ovim je crtanje građe čovječijeg tijela prema kanonu u frontalnoj i sagitalnoj
ravni, pomoćnim linijama, završeno (slika 4).

13
14
1.3
Crtanje biomehaničkih poluga
Preko već izvučenih pomoćnih linija, ucrtaju se biomehaničke poluge
i obrisi
glave linijama debljine od 0,4 - 0,8 mm i to:
1.3.1Frontalna ravan (
slika 5)
•
gornji dio velikog kruga glave R = ½ sbm,
•
tangente T i T1,
•
donji preostali dio malog kruga glave r = 1/3 sbm,
•
ramena osa, od centra desnog do centra lijevog zgloba ramena 3 - 4,
•
kičmeni stub, od tačke presjeka ramenske ose 3
- 4 i središnje ose tijela A
-
A do tačke presjeka karlične ose 1
- 2 i iste ose,
•
karlična osa, od centra desnog do centra lijevog zgloba kuka 1
- 2,
•
nadlaktica, od centra zgloba ramena do centra zgloba lakta 3 - 8 i 4 - 9,
•
podlaktica, od centra zgloba lakta do centra zgloba šake 8 - 10 i 9 - 11,
•
šaka, od centra zgloba šake do vrha srednjeg prsta 10 - 12 i 11 - 13,
•
natkoljenica, od centra zgloba kuka, do centra zgloba koljena 1 - 16 i 2 -
17,
•
potkoljenica, od c
entra zgloba koljena do centra skočnog zgloba 16
- 18 i
17 - 19,
•
stopalo, od centra skočnog zgloba do podloge 18
- 14 i 19 - 15.
1.3.2 Sagitalna ravan (slika 5)
•
lijepa polovina obima kruga R = ½ sbm sa centrom 27,
•
dio manjeg luka od desne strane manjeg kvadrata 35 do osnovne vertikale,
sa centrom luka u centru potiljačnog zgloba N1,
•
profil lica, odnosno veliki luk, od tačke presjeka manjeg luka i desne
stranice manjeg kvadrata 35 do donje stranice većeg kvadrata C1,
•
donja ivica donje vilice, od tačke C1 do tačke presjeka osnovne vertikale i
linije C1 - 36 (37),
•
zadnja ivica donje vilice, od tačke 37 do tačke presjeka linije 37
- 38 i
baze prvog submodula (E),
•
vratni dio kičmenog stuba, od centra potiljačnog zgloba N1 do grudne
krivine, sa centrom luka u t
ačci 42,
•
grudni dio kičmenog stuba, od donjeg dijela vratne krivine do gornjeg
dijela slabinske krivine, sa centrom luka u tačci 40,
•
slabimski dio kičmenog stuba, od donjeg dijela grudne krivine do centra
spoja sa
karlicom 25, sa centrom luka u tačci 41,
•
karlična osa, od centra spoja karlice i kičmenog stuba 25 do centra zgloba
kuka 23,

16
2. ODREĐIVANJE TEŽIŠTA ČOVJEČIJEG TIJELA U RAVNI
(zadatak br. 2)
Uvodni dio sa historijskim pregledom o određivanju težišta tijela čovjeka biće u
ovom praktikumu
izostavljen i izložen, uglavnom, praktični postupak
određivanja težišta tijela po pravilu slaganja paralelnih sila, računskim
(analitičkim) putem i verižnim poligonom. Opširnija teorijska objašnjenja data
su u udžbeniku „Biomehanika sportske lokomocije“ od prof. dr Branimira
Mikića i prof. dr Gruje Bjekovića.
Da bi se u svakom trenutku nekog od kretanja čovjeka ili stava i položaja mogla
odrediti pozicija težišta tijela u ravni, potrebno je raspolagati sa:
•
filmskim ili fotografskim snimkom aktuelnog položaja u sagitalnoj ravni,
•
filmskim ili fotografskim snimkom istog položaja u frontalnoj ravni,
•
tjelesnom težinom snimljene osobe,
•
tablicama koeficijenata za određivanje težine pojedinih dijelova tijela,
•
tablicama koeficijenata za određivanje rastojanja težišta
pojedinih dijelova
tijela od centra proksimalnog zgloba.
U zadatku br. 2 ovog praktikuma, kao i na praktičnom dijelu ispita, težište tijela
čovjeka određuje se samo u jednoj ravni.
Određivanje težišta tijela u ispitnom zadatku ne obavlja se na fotografsko
m
snimku, već na listu providnog papira (paus papira) na koju se sa fotografije
prenose centri zglobova, uzdužne ose pojedinih dijelova tijela i težišta za šake i
glavu. Pored fotografskog snimka određenog položaja i lista providnog papira,
kandidat dobija i tabelu u kojoj se nalaze zaokružene vrijednosti koeficijenata po
Fišeru i Braunu, odnosno Bernštajnu za određivanje položaja težišta i težina
pojedinih dijelova tijela.
Postupak određivanja težišta tijela u zadatku ovog praktikuma i zadacima na
praktičnom dijelu ispita (načelno), odvijao bi se u četiri faze.
•
određivanje centara zglobova, uzdužnih osa pojedinih dijelova tijela i
težišta šake i glave.
•
određivanje težišta pojedinih dijelova tijela.
•
određivanje težina pojedinih dijelova tijela.
•
određivanje težišta tijela jednim od načina (u praktikumu je obrađeno
određivanje težišta slaganjem paralelnih sila, računskim
-
analitičkim
putem, verižnim poligonom i kombinovanom metodom.
17
2.1 Određivanje centara zglobova, uzdužnih osa pojedinih dijelova tijela
i
težišta glave i šake
Da bi se odredio položaj i veličina središnjih osa pojedinih dijelova tijela,
potrebno je poznavati mjesta centara zglobova koji se određuju prema
karakterističnim tačkama tijela.
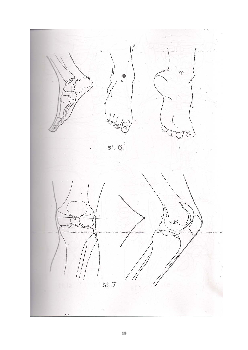
Stopalo se pretstavlja osom od zadnje ivice petne kosti do vrha drugog prsta
(slika 6).
Uzdužna osa potkoljenice nalazi se na liniji koja spaja centar skočnog zgloba i
centar zgloba koljena. Centar skočnog zgloba, za položaj tijela u sagitalnoj
ravni, poklapa se sa središtem ispupčenja gležnja. Za položaj tijela
u frontalnoj
ravni centar skočnog zgloba leži na sredini linije koja spaja središnje tačke oba
gležnja. Centar zgloba koljena, za položaj tijela u sagitalnoj i frontalnoj ravni,
poklapa se sa tačkom koja se nalazi u nivou donje ivice čašice na sredini nog
e
(slika 6 i 7).
Veličina uzdužne ose natkoljenice odgovara rastojanju od centra zgloba koljena
do centra zgloba kuka. Centar zgloba kuka, za položaj tijela u sagitalnoj ravni,
određuje se prema gornjoj ivici velikog trohantera i centra luka velikog
sjedal
nog mišića. Središnja osa natkoljenice mora približno da polovi
natkoljenicu po širini. Centri zglobova kukova, za položaj tijela u frontalnoj
ravni, nalaze se na presjeku uzdužnih osa buta i linije koja spaja gornje ivice
velikih trohantera (slika 10).
Tr
up se predstavlja osom od centra zgloba kuka do centra potiljačnog zgloba, za
položaj tijela u sagitalnoj ravni. Za položaj tijela u frontalnoj ravni, uzdužna osa
spaja centar potiljačnog zgloba i tačku na sredini karlične ose. Centar
potiljačnog zgloba na
lazi se približno u visini donje ivice slušne školjke na
sredini vrata (8, 9, 15 i 16).
Uzdužna osa nadlaktice nalazi se na liniji koja spaja centar zgloba ramena sa
centrom zgloba lakta. Centar zgloba ramena, za položaj tijela u sagitalnoj ravni,
određuje
se prema centru zaobljenja ramena kada je ruka u priručenju, a za
položaj ruke u uzručenju prema pazušnoj jami. Centar zgloba ramena, za
položaje tijela u frontalnoj ravni, nalazi se na presjeku uzdužnih osa nadlaktice i
ramenske ose (odredi se procjenom
prema deltastom mišiću). Centar zgloba
lakta nalazi se u nivou sredine olekranona na uzdužnoj osi nadlaktice tj.
podlaktice (slika 12 i 13).
Podlaktica je pretstavljena osom od centra zgloba lakta do centra zgloba šake.
Centar zgloba nalazi se u nivou šiljolikog nastavka lakatnice na uzdužnoj osi
podlaktice (slika 14).

19
20

22
2.2
Određivanje težišta pojedinih dijelova tijela
Za razliku od određivanja težišta glave i šake, sva ostala težišta relativno
kompaktnih dijelova čovječijeg tijela određuju se računskim putem, prema
zaokruženim koeficijentima W. BRAUNEA, O. FISCHERA i N.
BERNSTEINA.
Težišta pojedinih dijelova tijela sa izuzetkom težišta za glavu, šaku i stopalo,
nalaze se na uzdužnoj osi koja povezuje centre dva susjedna zgloba i bliža su
proksimalnom zglobu (za stopalo bliže peti), odnosno onom zglobu koji je
anatomski bliži kičmenom stubu. Tako je proksimalni zglob za potkoljenicu
zglob koljena, za natkoljenicu zglob kuka, za podlakticu zglob lakta, za
nadlakticu zglog ramena i za trup zglob kuka.
Rastojanje težišta pojedinih dijelova tijela od centra proksimalnog zgloba
odgovara proizvodu dužine uzdužne ose i koeficijenta za težišta odgovarajućeg
dijela tijela.
Za primjer zadatka u praktikumu kao i na praktičnom dijelu ispita, dužina
uzdužne ose izmjeri se u mm sa dozvoljenom tolerancijom od 0,30 mm i upiše u
tabelu 1,2 i 3 kolona 3 za odgovarajući dio tijela. Množenjem izmjerene dužine
uzdužne ose sa koeficijentom za težišta dijelova tijela, dobija se rastojanje
težišta od centra proksimalnog zgloba u mm. Dobijene vrijednosti upisuju se u
kolonu 4 i nanos
e na uzdužne ose skice čovjeka precrtane na paus papir. Težišta
pojedinih dijelova tijela obilježe se na isti način kao što je to učinjeno za težišta
glave i šake.
2.3
Određivanje težina pojedinih dijelova tijela
Kada se odrede težišta, odnosno napadne tačke
sile teže pojedinih dijelova tijela,
potrebno je odrediti i intenzitete sila koje dejstvuju na tačke, odnosno težinu
dijelova tijela.
Množenjem tjelesne težine (za slučaj u praktikumu 100 kp) sa koeficijentom za
određivanje težine dijelova tijela (tabela
1, 2 i 3 kolone 5) odredi se težina
posebno za svaki dio tijela i upiše u kolonu 7.
U ispitnom zadatku, na donjoj fotografiji, snimljeni su vježbači sa raznim
tjelesnim težinama.
23

25
26

28
2.4 Određivanje težišta čovječijeg tijela
2.4.1. Određivanje težišta čovječijeg tijela analitičkim putem
Napadna tačka težine svih dijelova tijela, odnosno težište tijela čovjeka može se
odrediti računskim putem kada se sistem sila proizvoljno stavi u koordinatni
sistem Oxy.
Određivanje težišta tijela ovim načinom zas
novano je na momentnom aksiomu
koji glasi: moment rezultante (proizvod najkraćeg rastojanja od težišta tijela
(TA) do koordinatne ose (xA i yA) i težine tijela jednaka je zbiru momenata svih
sila u datom sistemu (zbir svih proizvoda najkraćeg rastojanja od
težišta
odgovarajućeg dijela tijela do koordinatne ose i težine istog dijela tijela).
Rastojanje težišta tijela od y ose xA, za slučaj u praktikumu izračunava se prema
jednačini:
xA x GA = (Gc x xc) + (Gt x xt) + (dGf x dxf) + (sGf x sxf) + (dGs x dxs) +
(sGs x sxs) + (dGp x dxp) + (sGp x sxp) + (dGb x dxb) + (sGb x sxb) + (dGa x
dxa) + (sGa x sxa) + (dGm x dxm) + (sGm x sxm)xA x 100 = (6 x 20) + (46 x
73) + (12 x 119,5) + (12 x 103) + (4 x 152,8) + (4 x 111) + (2 x 187,5) + (2 x
140,3) + (3 x 56,2) + (3 x 56,2) + (2 x 69) + (2 x 69) + (1 x 59,5) + (1 x 59,5)xA
= 8591 / 100 = 85,91 mm
Rastojanje
težišta tijela od x ose yA, za slučaj u praktikumu izračunava se prema
jednačini:
yA x GA = (Gc x yc) + (Gt x yt) + (dGf x dyf) + (sGf x syf) + (dGs x dys) +
(sGs x sys) + (dGp x dyp) + (sGp x syp) + (dGb x dyb) + (sGb x syb) + (dGa x
dya) + (sGa x sya) + (dGm x dym) + (sGm x sym)yA x 100 = (6 x 85) + (46 x
103) + (12 x 92,2) + (12 x 94) + (4 x 48) + (4 x 49,5) + (2 x 22,8) + (2 x 22,1) +
(3 x 77,2) + (3 x 77,2) + (2 x 46,5) + (2 x 46,5) + (1 x 16,5) + (1 x 16,5)xA =
8644,4 / 100 =
86,44 mm
29
Postupa
k određivanja težišta tijela analitičkim putem na praktičnom dijelu ispita
i zadatku ovog praktikuma tekao bi ovim redom:
•
vježbač pretstavljen biomehaničkim polugama sa određenim težištima i
težinama pojedinih dijelova tijela stavi se proizvoljno u bilo koji od
kvadranata koordinatnog sistema Oxy (slika 17 (18)).
•
u daljem postupku slijedi ucrtavanje linija koje pretstavljaju najkraća
rastojanja od težišta pojedinih dijelova tijela do osa koordinatnog sistema
(izvučene linije zaklapaju sa apsisom i ordinatom
ugao od 90 stepeni). Ista
rastojanja se izmjere u mm i za y osu opisuju u tabelu 1, kolona 1, kolona
8, a za x osu u kolonu 10.
•
zatim se izmjerene vrijednosti najkraćeg rastojanja množe sa težinama
odgovarajućih dijelova tijela. Dobijeni proizvodi pretsta
vljaju momente u
odnosu na y i x osu i upisuju se u kolonu 9 i 11.
•
kada se izračunaju momenti svih sila, isti se zbrajaju posebno za y i x osu.
Zbir momenata se upisuje u tabelu 1, red 15, kolona 9 za momente u
odnosu na y osu i u kolonu 11 istog reda za momente u odnosu na x osu.
•
prema momentnom pravilu, najkraće rastojanje od težišta tijela (TA) do
osa y i x koordinatnog sistema dobija se kada se zbir momenata svih sila
posebno za obje ose podijeli sa težinom tijela (100 kp). Dobijene
vrijednosti se upisuju u red 16, kolona 9 za rastojanje težišta tijela od y
ose i kolonu 11 za rastojanje težišta tijela od x ose. Ista rastojanja se
određuju paralelnim linijama posebno sa ordinatom i posebno sa opisom.
Tačka u kojoj se ukrštaju pomenute linije (A i B) odgov
ara položaju težišta tijela
(slika 17 i 18).
2.4.2. Određivanje težišta čovjekovog tijela po pravilu o slaganju paralelnih
sila
Položaj zajedničkog težišta dva dijela tijela čovjeka izračunava se jednačinom
dobijenom prema momentnom prailu za
momentnu tačku u zajedničkom težištu
Tps (slika 19), gdje je:
•
Gp – težina stopala,
•
Gs – težina potkoljenice,
•
Gps – težina stopala i potkoljenice,
•
Tp – težina stopala,
•
Ts – težište potkoljenice,
•
Tps –
zajedničko težište stopala i potkoljenice,

31
32
2.4.2.1. Postupak slaganja težine dijelova tijela, tj. određivanja težišta tijela
(TA) po pravilu o slaganju paralelnih sila
Pošto se odrede težišta i težine pojedinih dijelova tijela, pristupa se slaganju
težina, odnosno određivanju težišta tijela (TA).Praktični postupak određivanja
težišta tijela po pravilu o slaganju paralelnih sila za primjer u praktikumu tekao
bi ovim redom (slika 20 (21)) i tabela br. 2.
2.4.2.1.1. Određivanje zajedničkog težišta stopala i potkoljenice desne noge
Polazeći uvijek od perifernih dijelova tijela, prvo se spoje pravom linijom
(transferzala dIps) težište stopala dTp i potkoljenice dTs desne noge.
Isto rastojanje izmjeri se u mm (dozvoljeno odstupanje od stvarne vrijednosti
0,30 mm) i zamijeni u jednačini 1. Također se zamijene i vrijednosti za težinu
stopala dGp = 2 kp i potkoljenice dGs = 4 kp.
dxps = dGs x dIps / dGs + dGp = 4 x 42,8 / 4 + 2 = 28,53 mm (1)
Dob
ijena vrijednost za dxps nanosi se po liniji dIps od napadne tačke one sile
teže kojoj odgovara krak dxps tj. od težišta stopala desne noge. Određeno
zajedničko težište za stopalo i potkoljenicu dTps obilježi se sa dvije ukrštene
linije dužine oko 3 mm.
2.
4.2.1.2. Određivanje zajedničkog težišta stopala, potkoljenice i natkoljenice
desne noge
Zajedničko težište stopala i potkoljenice dTps spoji se pravom linijom dIpsf sa
težištem natkoljenice dTf desne noge, izmjeri u mm, i sa vrijednostima za težinu
stopala i potkoljenice dGps = 6 kp i težinu buta dGf = 12 kp zamijeni u jednačini
2 i izračuna dxpsf.
dxpsf = dGf x dIpsf / dGf + dGps = 12 x 69, 5 / 12 + 6 = 46,33 mm
(2)
Vrijednosti za dxpsf nanosi se po liniji dIpsf od zajedničkog težišta i
po
tkoljenice dTps. Određena tačka odgovara položaju težišta desne noge dTpsf.

34
35

37
Vrijednost za dxma nanosi se
na liniju dIma od napadne tačke sile teže za šaku
dTm. Određena tačka odgovara položaju zajedničkog težišta šake i podlaktice
desne ruke dTma.
2.4.2.1.7. Određivanje zajedničkog težišta šake, podlaktice i nadlaktice desne
ruke
Zajedničko t
ežište šake i podlaktice dTma spoji se transferzalom dImab sa
težištem nadlaktice dTb, isto rastojanje izmjeri u mm i sa težinom šake i
podlaktice dGma = 3 kp i nadlaktice dGb = 3 kp zamijeni u jednačini 6.
Dxmab = dGb x dImab / dGb + dGma = 3 x 41,6 / 3 + 3 = 20,8 mm (6)
Vrijednost za dxmab nanosi se na liniju dImab od zajedničkog težišta za šaku i
podlakticu dTma. Određena tačka odgovara položaju težišta desne ruke dTmab.
Zahvaljujući činjenici da je zajednička težina šake i podlaktice jednaka težini
nadl
aktice, težište ruke dTmab određuje se geometrijski na sredini transferzale
dTmab.
2.4.2.1.8. Određivanje zajedničkog težišta šake i podlaktice lijeve ruke
Napadna tačka sile teže šake sTm spoji se linijom sIma sa napadnom tačkom
sile teže podlaktice sTa, isto rastojanje izmjeri u mm i sa težinom šake sGm = 1
kp i podlaktice sga = 2 kp zamijeni u jednačini 7.
sxma = sGa x sIma / sGa + sGm = 2 x 27,5 / 2 + 1 = 18,33 mm (7)
Vrijednost za sxma nanosi se na liniju sIma od težišta šake sTm. Određena tačka
odgov
ara položaju zajedničkog težišta šake i podlaktice lijeve ruke sTma.
2.4.2.1.9. Određivanje zajedničkog težišta šake, podlaktice i nadlaktice lijeve
ruke
Isto kao i za desnu ruku, težište lijeve ruke se određuje geometrijski na sredini
linije sImab, odnosno ½ sImab iznosi 19 mm.
2.4.2.1.10. Određivanje zajedničkog težišta obje ruke
Pošto možemo smatrati da je težina lijeve i desne ruke ista, zajedničko težište
obje ruke određuje se geometrijski na sredini linije Ies koja spaja težišta obje
ruke.
38
2.4.2.1.11. Određivanje zajedničkog težišta obje ruke i glave
Zajedničko težište za obje ruke Tes spoji se transferzalom Iesc sa težištem glave
Tc. Isto rastojanje izmjeri u mm i sa težinom za obje ruke Ges = 12 kp i glave
Gc = 6 kp zamijeni u jedna
čini 8.
xesc = Gc x Iesc / Gc + Ges = 6 x 41,2 / 6 + 12 = 13,73 mm (8)
Vrijednost za xesc nanosi se na liniju Iesc od zajedničkog težišta za obje ruke
Tes. Određena tačka odgovara položaju zajedničkog težišta za obje ruke i glavu
Tesc.
2.4.2.1.12. Određivanje zajedničkog težišta obje ruke, glave i trupa
Zajedničko težište za obje ruke i glavu Tesc spoji se linijom Icr sa težištem trupa
Tt. Isto rastojanje izmjeri u mm i sa zajedničkom težinom za obje ruke i glavu
Gesc = 18 kp i trupa Gt = 46 kp zamijeni u
jednačini 9.
xcr = Gt x Icr / Gt + Gesc = 46 x 50 / 46 + 18 = 35,93 mm (9)
Vrijednost za xcr nanosi se na liniju Icr od zajedničkog težišta obje ruke i glave
Tesc. Određena tačka odgovara položaju zajedničkog težišta za obje ruke, glavu
i trup, odnosno kranijalnog dijela tijela Tcr.
2.4.2.1.13. Određivanje težišta tijela
Težište kranijalnog dijela tijela Tcr spoji se transferzalom IA sa težištem
kaudalnog dijela tijela Tca. Isto rastojanje se izmjeri u mm i sa težinom
kranijalnog dijela tijela Gcr = 64 kp i kaudalnog dijela tijela Gca = 36 kp
zamijeni u jednačini 10.
xA = Gcr x IA / Gcr + Gca = 64 x 60 / 64 + 36 = 38,40 mm (10)
Vrijednost za xA nanosi se na liniju IA od težišta kaudalnog dijela tijela Tca.
Određena tačka odgovara položaju težišta tijela TA.

40
41

43
2.4.4.2. Određivanje zajedničkog težišta stopala, potkoljenice i natkoljenice
desne noge
Zamijenom vrijedn
osti u jednačini (2) isto kao u zadatku 2.4.2.1.3. dobiće se:
dxpsf = dGf x dIpsf / dGf + Gps = 8,4 x 53 / 8,4 + 4,2 = 35,33 mm (2)
Vrijednost za dxpsf nanosi se po transferzali dIpsf od zajedničkog težišta za
stopalo i potkoljenicu dTps. Određena tačka o
dgovara položaju težišta desne
noge Tpsf.
2.4.4.3. Određivanje zajedničkog težišta stopala i potkoljenice lijeve noge
Na isti način kao u zadatku 2.4.2.1.3. zamijenom odgovarajućih vrijednosti u
jednačini 3, dobiće se:
sxps = sGs x sIps / sGs + sGp = 2,8 x 30 / 2,8 + 1,4 = 20 mm (3)
Vrijednost sxps nanosi se na liniju sIps od težišta stopala sTp. Dobijena tačka
odgovara poziciji zajedničkog težišta za stopalo i potkoljenicu lijeve noge.
2.4.4.4. Određivanje zajedničkog težišta stopala, potkoljenice i natk
oljenice
lijeve noge
Zamijenom vrijednosti za sIpsf, sGps i Gf u jednačini 4 dobiće se:
sxpsf = sGf x sIpsf / sGf + sGps = 8,4 x 47 / 8,4 + 4,2 = 31,33 mm (4)
Vrijednost sxpsf nanosi se na liniju sIpsf od zajedničkog težišta stopala i
potkolje
nice sTps. Određena tačka odgovara poziciji težišta lijeve noge.
2.4.4.5. Određivanje zajedničkog težišta za obje noge
Isto tako kao u zadatku 2.4.2.1.5. zajedničko težište obje noge se odredi
geometrijski na sredini linije Ica.
44

46
2.4.4.6. Određivanje zajedničkog težišta šake i podlaktice desne ruke
Zamijenom vrijednosti za dIma, dGm i dGa u jednačini 5, dobiće se:
dxma = dGa x dIma / dGa + Gm = 1,4 x 25,2 / 1,4 + 0,7 = 17 mm (5)
Vrijednost dxma nanosi se na liniju dIma od
težišta šake dTma. Određena tačka
odgovara zajedničkom težištu šake i podlaktice desne ruke.
2.4.4.7. Određivanje zajedničkog težišta šake i podlaktice lijeve ruke
Zamijenom vrijednosti sIma, sgm i sGa u jednačini 6 dobiće se:
sxma = sGa x sIma / sGa + sGm = 1,4 x 26,8 / 1,4 + 0,7 = 17,86 mm (6)
Vrijednost sxma nanosi se na liniju sIma od težišta šake sTm. Određena tačka
odgovara zajedničkom težištu šake i podlaktice lijeve ruke.
2.4.4.8. Određivanje zajedničkog težišta šake, podlaktice i nadlaktice desn
e i
lijeve ruke
Isto tako, kao u zadatku 2.4.2.1.9. težište ruke se određuje geometrijski na
sredini linije dimab odnosno sImab.
2.4.4.9. Određivanje zajedničkog težišta za obje ruke
Zajedničko težište Tes određuje se geometrijski na sredini
linije Ies.
2.4.4.10. Određivanje zajedničkog težišta za obje ruke i glavuZamijenom
vrijednosti za Iesc, težinu glave Gc i težinu obje ruke Ges u jednačini 8, dobiće
se:
xesc = Gc x Iesc / Gc + Ges = 4,2 x 33,7 / 4,2 + 8,4 = 11,23 mm (8)
Vrijednost xesc n
anosi se na liniju Iesc od zajedničkog težišta za obje ruke Tes.
Određena tačka odgovara položaju zajedničkog težišta za obje ruke i glavu Tesc.
47
2.4.4.11. Određivanje zajedničkog težišta nogu, ruku i glave i trupa odnosno
težišta tijela analitičkim putem
Rastojanje težišta tijela TA od x i y ose koordinatnog sistema, izračunava se iz
momentnog aksioma koji glasi: moment rezultante (proizvod najkraćeg
rastojanja od težišta tijela do koordinatne ose xA, yA i težine tijela GA) jednak
je zbiru momenata svih sila u datom sistemu (zbir svih proizvoda najkraćeg
rastojanja od težišta odgovarajućeg dijela tijela do koordinatne ose i težine istog
dijela tijela). Odnosno, rastojanje težišta tijela TA od x ose yA izračunava se
prema:
yA = (Gesc x yesc) + (Gca x yca) + (Gt x yt) / GA
yA = (12,6 x 73,8) + (25,2 x 75) + (32,2 x 102,5) / 70 = 87,43 mm
Rastojanje težišta tijela TA od y ose xA izračunava se prema jednačini:
xA = (Gesc x xesc) + (Gca x xca) + (Gt x xt) / GA
xA = (12,6 x 61) + (25,2 x 144) + (32,2 x 104) / 70 =
110,6 mm
Postupak određivanja zajedničkog težišta za noge, ruke i glavu i za trup odnosno
težište tijela TA analitičkim putem tekao bi ovim redom.
Određena težišta slaganjem paralelnih sila Tca, Tesc i Tt, kao i t
ežine Gca, Gesc
i Gt stave se proizvoljno u bilo koji od kvadranata koordinatnog sistema Oxy
(slika 24 (25)).
U daljem postupku izvuku se uspravne linije (najkraća rastojanja) od aktuelnih
težišta do ose koordinatnog sistema. Ista rastojanja se izmjere u mm i
zamjenjuju u jednačini za yA i xA (tabela 3).
Zatim se izmjerene vrijednosti najkraćeg rastojanja množe sa težinama
navedenih dijelova tijela (Gesc, Gca i Gt). Dobijeni proizvodi predstavljaju
momente u odnosu na x i y osu.
Dalje, momenti svih sila zbrajaju se posebno za x i y osu i prema momentnom
pravilu dobijeni zbir momenata dijeli se sa težinom tijela GA = 70 kp. Dobijene
vrijednosti predstavljaju najkraća rastojanja od osa koordinatnog sistema do
težišta tijela xA i yA i nanose se od osa koordinatnog sistema.
Tačka u presjeku linija A i B odgovara položaju težišta tijela TA.

49
50
Odnos veličina na crtežu i u prirodnoj veličini je 1 :14. Razmjera u kojoj su
prikazani vektori sila teže iznosi 1 kp : 1,5 mm.
U spitnom zadatku pri određivanju težišta tijela izosta
vlja se obilježavanje
slovima i brojevima, kako je to prikazano na crtežima 17, 20, 22 i 24.
Definitivan izgled zadatka br. 2 prikazan je na slici 18, 21, 23, 25 i 26.
2.5.
Signatura konematičkog modela u kinematografskoj metodi
dp – desno stopalo,
sp – lijevo stopalo,
ds – desna potkoljenica,
ss – lijeva potkoljenica,
df – desna natkoljenica,
sf – lijeva natkoljenica,
t – trup,
c – glava,
dm – desna šaka,
sm – lijeva šaka,
da – desna podlaktica,
sa – lijeva podlaktica,
db – desna nadlaktica,
sb – lijeva nadlaktica,
dTp – težište desnog stopala,
sTp – težište lijevog stopala,
dTs – težište desne potkoljenice,
sTs – težište lijeve potkoljenice,
dTf – težište desne natkoljenice,
sTf – težište lijeve natkoljenice,
Tt – težište trupa,

52
dTmab – težište desne ruke,
sTmab – težište lijeve ruke,
Tca – težište nogu,
Tes – težište ruku,
Tesc – težište ruku i glave,
Tcr – težište ruku, glave i trupa,
TA – težište tijela,
TAs – težište tijela i sprave (opreme),
dGps – težina desne potkoljenice i stopala,
sGps – težina lijeve potkoljenice i stopala,
dGpsf – težina desne noge,
sGpsf – težina lijeve noge,
dGma – težina desne šake i podlaktice,
sGma – težina lijeve šake i podlaktice,
dGmab – težina desne ruke,
sGmab – težina lijeve ruke,
Gca – težina nogu,
Ges – težina ruku,
Gesc – težina ruku i glave,
Gcr – težina ruku, glave i trupa,
GA – težina tijela,
GAs – težina tijela i sprave (opreme),
dIps – transferzala I od težišta stopala do težišta potkoljenice desne noge,
sIps – transferzala I od težišta stopala do težišta potkoljenice lijeve noge,
dIpsf – transferzala I od težišta stopala i potkoljenice do težišta natkoljenice
desne noge,
sIpsf – transferzala I od težišta stopala i potkoljenice do težišta natkoljenice
53
lijeve noge,
dIma – transferzala I od težišta šake do težišta podlaktice desne ruke,
sIma – transferzala I od težišta šake do težišta podlaktice lijeve ruke,
dImab – transferzala I od težišta šake i podlaktice do težišta nadlaktice desne
ruke,
sImab – transferzala I od težišta šake i podlaktice do težišta nadlaktice lijeve
ruke,
Iesc – transferzala I od težišta ruku do težišta glave,
Icr – transferzala I od težišta glave i ruku do težišta trupa,
IA – transferzala I od težišta glave, ruku i trupa do težišta nogu,
Ias – transferzala I od težišta tijela do težišta sprave (opreme),
art. dtc –
desni skočni zglob,
art. stc –
lijevi skočni zglob,
art. dge – desni koljeni zglob,
art. sge – lijevi koljeni zglob,
art. dco – desni zglob kuka,
art. sco – lijevi zglob kuka,
art. dma – desni zglob korijena šake,
art. sma – lijevi zglob korijena šake,
art. dcu – desni zglob lakta,
art. scu – lijevi zglob lakta,
art. dhu – desni zglob ramena,
art. shu – lijevi zglob ramena,
art. ao –
potiljačni zglob,
art. cv –
zglobovi kičmenog stuba,
art. cvc –
zglobovi vratnog dijela kičmenog stuba,
art. cvt –
zglobovi grudnog dijela kičmenog stuba,

55
3.
PRAKTIČNI ZADACI
3.1.
Već smo odredili da je R = 680 N, pa je 680 N; X = 312 Nm; X = 0,46 m. S
obzirom da obje izvorne sile pokušavaju rotirati u smjeru kazaljke na satu oko
izabranog središta momenta rezultanta sila također ora pokuš
avati rotirati u
smjeru kazaljke na satu.
Primjer 1
Uzmimo tri paralelne sile koje djeluju okomito pre
ma dole čije su veličine s
lijeva na desno 320, 120 i 240 N. Udaljenost između sile od 320 N i 120 N je 0,6
m, a udaljenost između sila od 120 N i 240 N je 0,4 m (slika 1).
Pitanje:
Naći rezultantu triju sila
– jednostavnu silu koja bi imala jednako djelovanje kao
sve tri?
Odgovor:
Veličina rezultante je jednaka zbroju sila
R = suma F
To je R = 320 N + 120 N + 240 N = 680 N
Sad znamo veličinu rezultante. U ovom problemu sve sile djeluju u istom pravcu
pa i rezultanta također mora djelovati u tom pravcu, što je u ovom slučaju prema
dole. Preostala nepoznanica je položaj rezultante. Moramo primijeniti princip
momenta da bi smo odredili njezin položaj iz kojega ćemo izračunati momente.
Odabir mjesta koje ćemo odrediti kao središte momenta ili fukuluma
najpoželjije je da bude na pravcu djelovanja jedne od sila.
To eliminira jednu od nepoznanica iz jednadžbe pošto je udaljenost od te sile do
izabrane tačke nula. Ako izaberemo središte momenta na pravcu djelovanja sile
od 320 N.
Odredit ćemo X kao udaljenost od te
tačke do pravca djelovanja rezultante R.
Tada prema zakonu momenta R x X mora biti jednako zbroju momenata
izvornih sila oko središta momenta, a X će biti jednako zbroju tih momenata
podijeljeno sa R veličinom rezultante (slika 2).
RX = (120 N x 0,6 m) + (240 N x 1,0 m) = 72 Nm + 240 Nm = 312 Nm
56
Slika 1 A dijagram sistema sile Slika 2 Podlaktica kao trećerazredna poluga
Rezultanta djeluje prema dole pa se X udaljenost 0,46 m mora mjeriti na desno
od središta momenta da bi pravilno dobili pravac djelovanja rezultante, tj. Silu
koja djeluje prema dole rotirajućiu smjeru kazljke na satu. Sila prema gore
veličine 680 N koja djeluje na tom mjestu bila bi ekvilibrant ili sila reakcije da
bi mjesto održala u ravnoteži. Da prikažemo da središte oko kojeg djeluju
momenti može biti izabrano proizvoljno na bilo kojem mjestu ponovljeno
izračunavanje pokazat će da je x = 0,54 m. Ovdje sile djeluju u smjeru
suprotnom od kazaljki na satu oko izabranog središta momenta zbog toga
rezultanta mora biti smještena 0,54 m u lijevo od te tačke ili tačnije do mjesta do
kojeg se došlo u prethodnom rješenju.
Slika 3 Drugo rješenje primjera 1 B položaj i veličina rezultante

58
u tačku prik + mjene jedne od nepoznatih sila. To smanjuje moment te sile na
nulu s obzirom da je njena udaljenost od mjesta okreta nula.
3.3. Primjer 3
Uzmimo primjer bicepsa koji djeluje na podlakticu kada lakat nije pod uglom od
90 stepeni, nego kada je podlaktica 30 stepeni ispod horizontale i biceps se u
odnosu na podlakticu postavlja pod ugao 45 stepeni.
Slika 5 S
tatičke sile oko lakatnog zgloba kada je podlaktica 30 stepeni ispod
horizontale
Mišić je na 5 cm od lakatnog zgloba, težina podlaktice od 20 N je centrirano 15
cm od lakta, a ruka drži teret od 40 N, 30 cm od središnjeg zgloba. Ako je
podlaktica u bilo kojem položaju osim vodoravnog gravitacija ne može djelovati
pri 90 stepeni na ruku. Komponenta njene sile će djelovati okomito. Slično
promjenom položaja biceps neće povlačiti podlakticu pri 90 stepeni nego će
činiti komponente sila kao što je prikazano već ranije.
Pitanje:
Kolika mišićna sila je potrebna da bi održala podlakticu u položaju 30 stepeni
ispod horizontale? Kolike su sile u zglobu lakta?
59
Odgovor:
Pošto sila gravitacije i djelovanje mišića nisu okomiti na podlakticu moramo
naći njohove okomit
e komponente. Po principu suplementarnih uglova vidimo
da i komponente okomite na podlakticu Wy i Ly čine uglove od 30 stepeni sa
silom gravitacije G i teretom L. Dobija se da je moment sile jednak proizvodu
ukupne sile okomite na udaljenost od pravca djelovanja do središta momenta
(slika 6). Izbor metode o traženju momenata je stvar dogovora.
Slika 6
Biceps B pri različitim tačkama savijanja lakta, prikazuje varijacije u
kraku poluge
Npr. na slici 7 teško bi bilo tačno izmjeriti udaljenost 1
- 1* pa bi se dala
prednost metodi koja je korištena u prethodnom primjeru.
Slika 7 Alternativna metoda izražavanja momenata koji ne uključuje nađene
pravougaone komponente

61
V=0,05 dm
3
=0,05 l = 5*10
-2
*10
-3
= 5*10
-5
m
3
A= 0,5 J=5*10
-1
J
P
1
=4*10
4
Pa
P
2
=?
A= V(P
1
-P
2
V
A
)/:V
= P
1
- P
2
P
2
=P
1
V
A
-
P
2
= 4*10
4
5
1
10
*
5
10
*
5
−
−
-
= 4*10
4
- 10
4
P
2
= 3*10
4
Pa
3.6 Primjer 6
Tijelo se baci koso u odnosu na zemlju početnom brzinom od 7,2 m/s.
Maksimalni domet u vis mu je 2,10m. Pod kojim uglom elevacije se mora baciti
tijelo?
h
m
=2,10m
V
o
=7,2m/s
α=?
h
max
g
v
2
sin
2
2
0
α
=
2gh
max
v
0
2
sin
2
α
sin
2
2
0
2
v
gh
α=
;
sinα=
2
2
,
7
1
,
2
*
10
*
2
;
sinα=
810
,
0
;
sinα=0,90
α=64,158˚
62
4. Mjerenje stava i tjelesnog stanja
4.1. Sagitalna ravan (ulegnuta ravan)
Uspravan kičmeni ugao je osnova prihvatljivog mirnog stava. Mišljenja
stručnjaka su različita pri objašnjenju „dobrog“ stava, pojma koji se veže za
štednju energije i kozmetičku prihvatljivost. Može se primijeniti mnogo
varijacija u grupama zdravih subjekata (osoba). Bitne individualne razlike mogu
se vidjeti u uspravnom i pognutom stavu i kod dubokog udisaja / izdisaja i važno
je standardizovati poziciju za svaku osobu pojedinačno onako kako je to opisano
u metodi.
Obje „ravna leđa“ i pretjerana zakrivljenost smatraju se problematičnim, jer su
povezane sa posljedicom bola u leđima
. Kifoza od 20 - 45 stepeni i lordoza od
40 - 60 stepeni smatraju se normalnim nizom (Roaf, 1960). Fon et al (1980)
ističe se da su ove brojke neodgovarajuće za djecu i tinejdžere jer se kičmeni luk
sa godinama mijenja. To je posljedica smanjenja elastičnosti kičmenih
ligamenata i promjena u sadržaju minerala u kostima.
Dvije praktične metode ovdje objašnjene često se koriste na klinikama za leđa i
nazivaju se
kifometrija
i
goniometrija.
Ovi eksperimenti će dati niz vrijednosti
koje opisuju / oblik/ stanje
leđa.
4.1.1. Oprema
1.Debrunerov kifometar (straumann Ltd, Welwyn Garden City, England or
Protek AG, Bern, Switzerland).
2.Gonometar, e.g. Myrin Goniometar (LIC Rehab., Solna, Sweden).
4.1.2. Metoda
Subjektu se daju instrukcije da stoji bos, spojenih peta u uspravnoj i opuštenoj
poziciji, da gleda pravo naprijed i normalno diše i da ruke vise opušteno uz
tijelo. Ramena bi trebala biti opuštena.
Debrunerov kifometar se sastoji od dva duga kraka, a ugao između ova dva
kraka je prenosi kroz paralelne potpornje do uglomjera.
(slike 1 i 2).
Kičmena
zakrivljenost bi se kifometrom trebala procijeniti kada osoba maksimalno
udahne vazduh i kada izdahne vazduh.

64
Slika 3 Goniometar mjeri Slika 4 Mjerenje ugla na Slika 5 Mjerenje nagetosti
nagib ugla, ugao između dodirnoj tački prsa i krsta (nagiba) ugla na dodirnoj
kičme i vertikale na nivou (slabine) tački k
rsta (slabine) i
sedmog zatiljnog pršljena krstačne kosti
Razlika između leđnog ugla i vertikale se mjeri sa pokazivačem na koji djeluje
gravitacija. Razlika između mjera na T1 i T2 pokazuje stepen kifoze i devijac
ije
među uglovima na T12 i S1 pokazuje stepen križne lordoze.
Korištenje kifometra ili goniometra dopušta mjerenje normalnih zavoja
kičmenog stuba. Ugao prsne kifoze i križne lordoze će pružiti korisne
informacije u vezi individualnog ili grupnog držanja tijela.
65
4.2. Procjena sjedećeg stava
Sjedeći stav se može procijeniti tako što subjekat postavimo na visoku stolicu.
Koljena bi trebala biti savijena do 90 stepeni i butine (bedra) do 90 stepeni,
zavisno od trupa. Većinu težine uzimaju bedrene kuglaste izbočine na kostima,
koje se ponašaju kao oslonac unutar zadnjice. Ako ugao kuka pređe 60 stepeni,
napetost koljene tetive se povećava i kičma kompenzira gubljenjem konkavnosti
lordoze u križnom dijelu kičme. Zbog toga udobna pozicija zahtijeva
razmatra
nje dužine cjevanice, bedrene kosti u donjem dijelu kičme (održavanje
lordoze donjeg dijela kičme je važno zbog izbjegavanja križne istegnutosti
izazvane stavom). Da bi se osigurala odgovarajuća stolica za osobu, istraživanje
ovih parametara može se lako poduzeti korištenjem antropometra i goniometra.
Bočno savijanje kičme može se procijeniti tako da se brojčanik goniometra
postavi preko pršljena T1 te da se osoba zamoli da se savije na desno i na lijevo.
Sagitalno savijanje se može izmjeriti goniometrom, a
li se češće mjeri i poljima
istraživanja pomoću tzv. testa „sjedi i dohvati“.
4.3. Bočne devijacije
4.3.1. Oprema
Skoliometar, e.g. Orthopedic Systems, Inc Hayward, California.
4.3.2. Metoda
Skoliometar se koristi za mjerenje bočnih devijacija kičme
– izraženih kao
asimetrični deformitet trupa. Koristi se u prsnom i križnom dijelu i ispostavilo se
da je manje osjetljiv za identifikaciju križne skolioze. Razlog je nejasan jer se
bočni kičmeni zavoj i osovinsko okretanje trupa također dešavaju u tom dijelu
(u
toj religiji). Bočne devijacije se najčešće pronalaze kod skolioze. Nestrukturalna
skolioza se može formirati nejednakom dužinom nogu i često je neprogresivno.
Strukturalna skolioza je ozbiljno stanje sa mogućnošću napredovanja bolesti u
periodu rasta.
Ako se ustanovi, takav slučaj bi se trebao hitno obratiti za
mišljenje ortopeda.
Osoba koja stoji zauzima naprijed nagnuti položaj da je trup otprilike paralelan
sa podom i da su stopala zajedno. Ruke se sa spojenim dlanovima drže između
koljena. Ovakva po
zicija nudi najproduktivnije rezultate u kliničkim
istraživanjima autora. Osoba koja vrši pregled postavlja skoliometar na leđa
pacijenta, tako da centar sprave odgovara centru konture trupa, duž kičmenog
stuba. Počevši od mjesta gdje se vrat spaja sa trupom, skoliometar se pokreće

67
Tabela 1 Primjerak formulara za prikupljanje podataka
Ime subjekta
M
Datum
09.06.95.
Datum rođenja
01.01.80.
Spol
Muški
Visina
1823.0 mm
Težina
73,6 kg
Test 1
Test 2
Kifometar
Ugao kifoze T1-T12
34.0 stepeni
32.4 stepeni
Ugao lordoze T12-S1
23.5 stepeni
24.5 stepeni
Goniometar
Gornji nagnuti ugao
37.0 stepeni
35.0 stepeni
Nagnuti ugao
-11.0 stepeni
-14.0 stepeni
Donji nagnuti ugao
-7.0 stepeni
-10.0 stepeni
Lordoza
30.0 stepeni
35.0 stepeni
Kifoza
20.0 stepeni
24.0 stepeni
Saviljivost
Sjedi i dohvati -
rezultat
20.0 stepeni
20.5 stepeni
Skoliometar
AT1
3.0 stepeni
5.0 stepeni
Bočna savitljivost
Desna strana
25.0 stepeni
23.0 stepeni
Lijeva strana
20.0 stepeni
20.0 stepeni
Dužina nogu
Ležeći položaj
Desna noga
980.0 mm
980.0 mm
Lijeva noga
970.0 mm
975.0 mm
Nejednakost
10.0 mm
5.0 mm
Stojeći
Desna noga
950.0 mm
955.0 mm
Lijeva noga
970.0 mm
950.0 mm
Nejednakost
5.0 mm
5.0 mm
68
5. LITERATURA
1.
Biberović, A. (2007):
Biomehanik
a, Tuzla.
2.
Bubanj, R. (1998):
Osnove primijenjene biomehanike u sportu,
SIA, Novi
Sad.
3.Bubanj, R. (2000):
Osnove primijenjene biomehanike u kineziologiji
, SIA,
Novi Sad.
4.Jarić, S. (1997):
Biomehanika humane lokomocije sa biomehaniko sporta
,
Beograd.
5.Jovović, V. (2003
): Biomehanika sportske lokomocije,
Filozofski fakultet,
Nikšić, Odsjek za fizičku kulturu.
6.Mikić, B., Hadzić, M. (1997):
Biomehanika, I izdanje,
Filozofski fakultet,
Tuzla.
7.Mikić, B., Bjeković, G. (2004):
Biomehanika sportske lokomocije
, Fakultet za
tjelesni odgoj i sport Univerziteta u Tuzli, Tuzla.
8. Opavski, P. (1962):
Osnovi biomehanike
, Zavod za izdavanje udžbenika
Srbije, Beograd.
Želiš da pročitaš svih 1 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































