1
Sadržaj:
1.
Uvod
1.1.
Vrednost broja
1.2.
Broj u matematici
1.3.
Broj u fizici
2.
Osobine broja
2.1.
Iracionalnost
2.2.
Transcendentnost
2.3.
Hronološki prikaz vrednosti broja
2.4.
Istorijat broja
3.
Izračunavanje broja pomoću računara
3.1.
Čudnovski algoritam
3.2.
Lajbnicov algoritam
3.3.
Gausov algoritam
3.4.
Spigotov algoritam
3.5.
Liu Huijev algoritam
4.
Zanimljivosti
5.
Zaključak
6.
Izvori saznanja
2
1.
Uvod
Broj π je matematička konstanta koja definiše odnos obima i prečnika kruga ili kao
odnos površine i kvadrata poluprečnika kruga.
Slika 1.1.
Odnos obima i prečnika kruga
Slika 1.2.
Odnos površine i kvadrata poluprečnika
Broj π je poznat i kao Arhimedova konstanta (prema grčkom matematičaru
Arhimedu) ili Ludolfov broj (prema nemačkom matematičaru Ludolfu van Cojlenu). Simbol
za Arhimedovu konstantu prvi put je uveo 1706. godine matematičar Vilijam Džons kada je
objavio delo “Novi uvod u matematiku”. Ova oznaka je postala standardna nakon što ju je
usvojio Leonard Ojler. π je početno slovo grčke reči
περιφέρεια
što znači obod,
περιμετρος
što znači meriti okolo. Broj π se pojavljuje kako u matematici, tako i mnogim
naukama.
1.1. Vrednost broja π
Numerička vrednost broja π zaokružena na 64 decimalna mesta je
Iako je vrednost broja π izračunata na više od bilion decimala za osnovne primene u
matematici i fizici dovoljno dobra vrednost je 3,14. Na primer, vrednost zaokružena na 11
4
2.
Osobine broja π
Najvažnije osobine broja π su da je iracionalan i transcendentan.
2.1. Iracionalnost
Broj π je iracionalan broj što znači da se ne može izraziti kao odnos dva cela broja, tj.
ne može se napisati u obliku razlomka (a/b)
,
gde su
a
i
b
celi brojevi. To znači da se broj π
predstavlja beskonačnim nizom cifara i to tako da nema periodičnog ponavljanja cifara.
Dokaz za iracionalnost broja π je izveo 1761. godine švajcarski matematičar i fizičar Johan
Hajnrih Lambert.
2.2.
Transcendentnost
Broj
je transcendentan broj što znači da nije rešenje nijedne algebarske jednačine
čiji su koeficijenti celi brojevi. Dokaz za transcendentnost izveo je 1882. godine nemački
matematičar Karl Luis Ferdinand fon Lindeman. Posledica transcendentnosti je da se π ne
može izraziti korišćenjem konačnog broja celih brojeva uz četiri osnovne računske operacije,
što još znači da nije moguće izvršiti kvadraturu kruga, tj. nemoguće je lenjirom i šestarom
konstruisati kvadrat čija bi površina bila jednaka površini datog kruga.
5
3.
Hronološki prikaz vrednosti broja
matematičar
datum
dec.mesta
vrednost
1 Rindov papirus
2000 p.n.e. 1
3.16045 (4(8/9)
2
)
Arhimed
250 p.n.e.
3
3.1418
3 Vitruvijus
20 p.n.e.
1
3.125 (25/8)
4 Čang Hong
130
1
3.1622 (
)
5 Ptolomej
150
3
3.14166
6 Vang Fan
250
1
3.155555 (142/45)
7 Liu Hui
263
5
3.14159
8 Tsu Čung Či
480
7
3.141592920 ( 355/113)
9 Arjabhata
499
4
3.1416 (62832/2000)
10 Bramagupta
640
1
3.1622 (
)
11 Al Horezmi
800
4
3.1416
12 Fibonači
1220
3
3.141818
13 Madhava
1400
11
3.14159265359
14 Al Kaši
1430
14
3.14159265358979
15 Valentus Oto
1573
6
3.1415929
16 Fransoa Vijet
1593
9
3.1415926536
17 Adrijan Van
Romen
1593
15
3.141592653589793
18 Van Cojlen
1596
20
3.14159265358979323846
19 Van Cojlen
1596
35
3.1415926535897932384626
433832795029
20 Isak Njutn
1665
16
3.1415926535897932
21 Abraham Šarp
1699
71
7
45 Šigeru Kondo
2013
12.000.000.000.050
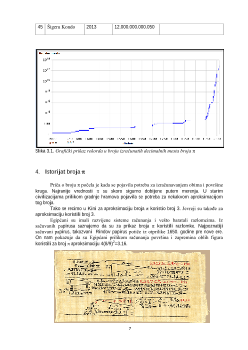
Slika 3.1. Grafički prikaz rekorda u broju izračunatih decimalnih mesta broja
π
4.
Istorijat broja
Priča o broju π počela je kada se pojavila potreba za izračunavanjem obima i površine
kruga. Najranije vrednosti
su skoro sigurno dobijene putem merenja. U starim
civilizacijama prilikom gradnje hramova pojavila se potreba za nekakvom aproksimacijom
tog broja.
Tako se recimo u Kini za aproksimaciju broja π koristio broj 3. Jevreji su takođe za
aproksimaciju koristili broj 3.
Egipćani su imali razvijene sisteme računanja i vešto baratali razlomcima. Iz
sačuvanih papirusa saznajemo da su za prikaz broja π koristili razlomke. Najpoznatiji
sačuvani papirus, takozvani Rindov papirus potiče iz otprilike 1650. godine pre nove ere.
On nam pokazuje da su Egipćani prilikom računanja površina i zapremina oblih figura
koristili za broj
aproksimaciju 4(8/9)
2
=3.16.
