Dr Mirjana Medenica

Dr Du{an Male{ev

Eksperimentalna

zi~ka hemija

Beograd, 2002.

EKSPERIMENTALNA FIZI^KA HEMIJA

Dr Mirjana Medenica, red. prof.

Dr Du{an Male{ev, red. prof.

Drugo izdanje

Recenzenti

Dr Dragan Veselinovi}, red. prof. u penziji

Fakultet za fizi~ku hemiju u Beogradu

Dr Zorica Radovi}, red. prof.

Farmaceutski fakultet u Beogradu

Odlukom dekana Farmaceutskog fakulteta u Beogradu broj 1527/2-BJR od 21. 09. 1998.

ova knjiga odobrena je kao univerzitetski ud`benik.

Izdava~

Dr Mirjana Medenica

Lektor

Mr Pejo Vukeli}

Fotografije

Branislav Nikoli}

Grafi~ko oblikovanje

Ilija Kne`evi}

Korice

Dr Mirjana Medenica

Tira` 1500

[tampa

Akademija {tamparija

, Narodnog fronta 43, Beograd

Sva prava zadr`ana. Nijedan deo ove knjige ne mo`e biti reprodukovan u bilo kom obliku

ili smislu bez pismenog odobrenja izdava~a i/ili autora.

ISBN 86-901485-4-X

Ud`benik

Eksperimentalna fizi~ka hemija

nastao je kao rezultat du-

gogodi{njeg rada sa studentima u laboratoriji Zavoda za fizi~ku he-

miju Farmaceutskog fakulteta Univerziteta u Beogradu. Prvenstveno

je namenjen studentima Farmaceutskog fakulteta za predmet

Fizi~ka

hemija i instrumentalne metode

Ud`benik sadr`i 11 tematskih poglavlja predvi|enih planom i

programom studija na Farmaceutskom fakultetu u Beogradu. Svako

teorijsko poglavlje (

Teorijski princip

) pra}eno je i odgovaraju}im

eksperimentima (

Uradite samostalno...

). Pristup svim eksperimen-

tima je isti, {to podrazumeva (

Zadatak ve`be

), neophodnu aparatu-

ru i hemikalije, opis pripreme eksperimenta

(Priprema

), neposred-

nu realizaciju eksperimenta uz detaljan opis aparature (

Postupak

) i

prikaz i obradu dobijenih rezultata merenja (

Rezultati

). Predvi|eno

je da student upisuje rezultate u odgovaraju}e tabele. Na kraju teksta,

u Prilogu knjige, date su tablice fizi~kohemijskih veli~ina i Statisti~ka

obrada rezultata.

Autori se zahvaljuju recenzentima prof. dr Draganu Veselinovi}u

i prof. dr Zorici Radovi} na veoma studioznom ~itanju rukopisa knji-

ge i korisnim savetima koje su doprinele pobolj{anju kvaliteta ruko-

pisa.

Branislav Nikoli} je svojim visoko profesionalnim fotografijama

doprineo kvalitetnoj ilustraciji instrumenata sa kojima se studenti

sre}u u laboratoriji.

Ilija Kne`evi} je svojim prefinjenim umetni~kim izrazom dopri-

neo grafi~kom oblikovanju ove knjige.

Zahvaljujemo se sponzorima koji su omogu}ili {tampanje drugog

izdanja ovog ud`benika.

Autori }e sa zahvalno{}u prihvatiti sve kriti~ke primedbe i suge-

stije ~italaca radi pobolj{anja kvaliteta ovog ud`benika u slede}im

izdanjima.

Beograd, 2002.

Autori

. Osobine rastvora

VISKOZNOST /3/

– Odre|ivanje viskoznosti metodom po Ostvaldu (12)

POVR[INSKI NAPON /15/

– Odre|ivanje povr{inskog napona te~nosti stalagmometrom (21)

Koligativne osobine rastvora

KRIOSKOPIJA /27/

– Odre|ivanje molarne mase (32)

Termi~ke osobine rastvora

KALORIMETRIJA /39/

– Odre|ivanje toplote rastvaranja (44)

Osobine molekula

REFRAKTOMETRIJA /49/

– Odre|ivanje molarne refrakcije rastvora (55)

POLARIMETRIJA /61/

– Odre|ivanje koncentracije rastvora saharoze (69)

Apsorpciona fotometrija

KOLORIMETRIJA /75/

– Odre|ivanje koncentracije obojenog rastvora (81)

FOTOMETRIJA /85/

– Odre|ivanje koncentracije obojenog rastvora (89)

SPEKTROFOTOMETRIJA /93/

– Odre|ivanje koncentracije rastvora metodom

kalibracione krive (100)

Elektroliza

ELEKTROLIZA /109/

– Provera Faradejevog zakona (113)

KULOMETRIJSKA TITRACIJA /115/

– Odre|ivanje koncentracije natrijum-tiosulfata (119)

SADR@AJ

107

Prilog

TABLICE /267/

STATISTI^KA OBRADA REZULTATA /277)

Literatura

Indeks

265

285

289

(1)

Osobine

rastvora

VISKOZNOST

Odre|ivanje viskoznosti

metodom po Ostvaldu

POVR[INSKI NAPON

Odre|ivanje povr{inskog napona te~nosti

stalagmometrom

Tako se Njutnova jedna~ina (1) mo`e jednostavnije prikazati:

Ako su povr{ina A i gradijent brzine V jedini~ne vrednosti, sledi

da je:

{to zna~i da je koeficijent viskoznosti ili, kra}e, viskoznost jedna-

ka sili unutra{njeg trenja. Ova viskoznost naziva se

apsolutna

ili

di-

nami~ka viskoznost

Jedinice dinami~ke viskoznosti izvode se iz Njutnovog zakona:

Paskal-sekund (Pa.s) je izvedena jedinica, a defini{e dinami~ku

viskoznost homogenog fluida koji laminarno struji i u kome, izme-

|u dva paralelna sloja na rastojanju od 1 m i gradijentom brzine od

1 (m/s)/m, nastaje napon smicanja od 1 paskala.

Recipro~na vrednost dinami~ke viskoznosti je

fluiditet

. To je

merilo lako}e kojom te~nost mo`e da te~e.

U tablici 1 date su vrednosti za dinami~ku viskoznost nekih te~-

nosti na 20°C.

Te~nost

(Pa s)

Ricinusovo ulje

0,986

Maslinovo ulje

0,084

Sulfatna kiselina

0,025

Salicilna kiselina

2,71×10

-3

Glicerol

1,49×10

-3

Etanol

1,20×10

-3

Voda

1,005×10

-3

Ksilol

0,81×10

-3

Toluol

0,59×10

-3

Benzen

6,52×10

-4

Hloroform

5,80×10

-4

Etar

2,33×10

-4

Medenica / Male{ev

blliic

a 1

1..

Dinami~ka viskoznost nekih

te~nosti na 20°C

F =

. A . V

(2)

F =

(3)

(=)

(=) N . m

–2

(=) Pa . s

A . V

m/s

Pored dinami~ke, definisana je i

kinemati~ka viskoznost

, koja

se ~e{}e koristi:

gde je

– gustina fluida.

Dinami~ka viskoznost koristi se za definisanje osobina samo ~is-

tih (jednokomponentnih) te~nosti, tzv. »njutnovskih sistema« koji

se pona{aju po Njutnovom zakonu, prikazanom jedna~inom (1).

Ostale te~nosti, tzv. heterogeni disperzni sistemi ne pona{aju se po

ovom zakonu i nazivaju se »nenjutnovskim sistemima«.

Ako se radi o binarnim sistemima, rastvorima, koriste se

relativ-

specifi~na

redukovana

unutra{nja viskoznost

Relativna viskoznost

(

) predstavlja koli~nik viskoznosti rast-

vora (

) i rastvara~a (

To je mera promene viskoznosti rastvora u odnosu na ~ist rast-

vara~ i zato je uvek ve}a od jedinice. IUPAC* preporu~uje da se ova

veli~ina naziva »viskozitetni koli~nik«.

Specifi~na viskoznost

(

) prikazuje prira{taj viskoznosti rast-

vora iznad jedinice, prouzrokovan prisustvom rastvorene materije:

Specifi~na viskoznost zavisi od vrste rastvara~a. Kako i relativna i

specifi~na viskoznost zavise od koncentracije, uveden je pojam

re-

dukovane viskoznosti

(

red

) koja predstavlja koli~nik specifi~ne

viskoznosti i koncentracije:

Redukovana viskoznost predstavlja prira{taj specifi~ne visko-

znosti po jedinici koncentracije. Za slu~aj da c

0 definisan je tzv.

grani~ni broj viskoznosti

ili

unutra{nja viskoznost

[η]

Eksperimentalna fizi~ka hemija

*International Union of Pure and

Applied Chemistry (

Internacionalna

unija za ~istu i primenjenu hemiju

)

(4)

(5)

– 1

–

(6)

red

(7)

[h]

lim

(8)

gde je:

M – molarna masa

– dinami~ka viskoznost

– gustina te~nosti

– gustina pare.

U tablici 2 date su vrednosti reohora za neke atome i atomske

grupe, pa se na osnovu aditivnosti mo`e izra~unati reohor slo`enijih

jedinjenja.

TOM

ATOMSKA GRUPA

EOHOR

12,8

H (u C–H)

5,5

H (u C–OH)

10,5

O (etarski)

10,0

21,3

35,8

23,8

COO (kiseline i estri)

36,0

Za farmaciju je poznavanje viskoznosti od velikog zna~aja pri-

likom formulacije farmaceutskih preparata i njihovih oblika za ade-

kvatnu primenu (emulzije, paste, supozitorije ili filmovi za oblagan-

je tableta). Proizvodnja medicinskih i kozmeti~kih krema, pasta i

losiona zahteva dobro poznavanje i reolo{kih osobina, kako bi pre-

parat bio pogodan da se primeni na ko`u. Ta~no definisani reolo{ki

parametri od presudnog su zna~aja prilikom izrade injekcionih hi-

podermijskih rastvora, da bi prilikom primene nesmetano proticali

kroz iglu.

Istiskivanje pasta iz tuba, pakovanje granuliranih preparata i

mnogi drugi postupci u farmaceutskoj industriji zahtevaju dobro

poznavanje zakona reologije.

Prou~avanje viskoznosti, kako pravih rastvora tako i koloidnih

disperznih sistema, pored teorijskog ima i prakti~no zna~enje. Me-

renjem viskoznosti koloidnih rastvora mogu}e je odrediti molarnu

masu koloida i objasniti oblik koloidnih ~estica. Ovo je veoma zna-

~ajno u proizvodnji rastvora za zamenu krvne plazme (npr. dekstra-

Eksperimentalna fizi~ka hemija

blliic

a 2

2..

Vrednosti reohora nekih atoma

i atomskih grupa

na). Pored ovoga, poznavanje viskoznosti va`no je i za predvi|anje

procesa apsorpcije leka iz gastrointestinalnog trakta.

Za odre|ivanje viskoznosti

koriste se ure|aji koji su zasnovani

na:

Poazejevom

(Poiseuille)

zakonu

za isticanje te~nosti kroz kapi-

larnu cev –

metoda kapilarne cevi

Stoksovom

(Stokes)

zakonu

za brzinu padanja kugle kroz stub

te~nosti –

metoda padanja tela

Ako se koeficijent viskoznosti odre|uje merenjem brzine istica-

nja te~nosti pod dejstvom Zemljine te`e (slika 4), onda je pritisak

stuba te~nosti

jednak sili

koja pod uticajem sile zemljine te`e

deluje na povr{inu popre~nog preseka stuba te~nosti

Kako je:

gde je:

h – visina stuba te~nosti

g – ubrzanje Zemljine te`e

– gustina te~nosti,

to se iz jedna~ina (12) i (13) dobija izraz za silu

, koja pod uti-

cajem sile Zemljine te`e vr{i smicanje slojeva:

Te~nost po~inje da isti~e kada se sila trenja

(jedna~ina 2), koja

spre~ava kretanje slojeva, izjedna~i sa silom

, koja pokre}e slojeve:

Medenica / Male{ev

Metoda kapilarne cevi

Slliik

a 4

4..

Metoda kapilarne cevi

p =

(12)

p = h . g .

(13)

= h . g .

. S

(14)

F = F

(15)

Deljenjem jedna~ina (19) i (20) i re{avanjem po

dobija se iz-

raz iz koga se izra~unava koeficijent viskoznosti:

gde je:

– koeficijent viskoznosti analizirane te~nosti

– koeficijent viskoznosti vode

– vreme isticanja analizirane te~nosti

– vreme isticanja vode

– gustina analizirane te~nosti

– gustina vode.

Primenjena je kod viskozimetra s kuglom, a zasniva se na Stokso-

vom zakonu:

gde je:

– koeficijent viskoznosti te~nosti

F – sila trenja pri kretanju kugle kroz stub te~nosti

r – polupre~nik kugle

v – brzina kretanja kugle (v = l/t, gde je

– du`ina stuba te~nosti,

– vreme padanja kugle).

Kugla pada pod dejstvom Zemljine te`e, a sila koja deluje na

kuglu jednaka je:

gde je:

g – ubrzanje Zemljine te`e

– gustina kugle

– gustina te~nosti.

Medenica / Male{ev

Metoda padanja tela

(21)

. g(

–

)

(23)

F =

. r . v

(22)

Kada se ove dve sile izjedna~e, kugla se kre}e uniformno kroz

te~nost brzinom

. Tada iz jedna~ina (22) i (23) sledi:

Kako su veli~ine u razlomku konstantne, to sledi izraz:

Za odre|ivanje viskoznosti po ovoj metodi koristi se

Heplerov

(Höppler)

viskozimetar

(slika 6).

Cev je napunjena te~no{}u poznate gustine. Kuglica, poznate gu-

stine, pada kroz cev ~iji je pre~nik neznatno ve}i od pre~nika kugli-

ce. Meri se vreme padanja kuglice izme|u ozna~enih linija A i B. Ceo

postupak izvodi se uz termostatiranje. Prethodno je potrebno (u

uputstvu za ure|aj) na}i vrednost konstante

za kuglice poznatih

gustina i pre~nika.

Eksperimentalna fizi~ka hemija

Slliik

a 6

6..

Heplerov viskozimetar

(

–

(24)

= K(

–

(25)

Preko gumenog nastavka vodu povu}i iznad gornje oznake na

viskozimetru i pustiti da slobodno proti~e kroz kapilaru. Hrono-

metar uklju~iti kada se menisk poklopi sa oznakom A, a isklju~iti ka-

da se menisk poklopi sa oznakom B na viskozimetru. Vreme isticanja,

izra`eno u sekundama, zapisati sa ta~no{}u hronometra. Merenje

vremena isticanja vode (t

) ponoviti deset puta. Viskozimetar za-

tim isprati sa malo etanola i osu{iti na vakuumu.

Postupak

Kao i kod kalibracije viskozimetra, suvom pipetom odmeriti istu za-

preminu analizirane te~nosti i izvr{iti deset merenja vremena isti-

canja analizirane te~nosti (t

) na istoj temperaturi.

Iz eksperimentalno dobijenih srednjih vrednosti vremena istica-

nja i datih vrednosti za gustinu i viskoznost vode (tablica 1 u Pri-

logu) izra~unati koeficijent viskoznosti (

Rezultate prikazati tabelarno.

Eksperimentalna fizi~ka hemija

t = ..... °C

V = ..... mL (odmerena zapremina te~nosti u viskozimetru)

t = .......°C

= ....... kg m

-3

(tabli~na vrednost)

= ....... Pa s (tabli~na vrednost)

Medenica / Male{ev

ella

a 2

2..

Gustina i koeficijent viskoznosti

analizirane teènosti

(kg m

-3

)

(Pa s)

Vreme (s)

voda

analizirana te~nost

ella

a 1

1..

Vreme isticanja

REZULTATI

Broj merenja

srednja vrednost

Te~nost

(N m

-1

) na 20°C

t.k. (°C)

Voda

0,0728

100

Benzol

0,0289

80,1

Toluol

0,0284

110,6

Hloroform

0,0271

61,0

Aceton

0,0237

56,5

Metanol

0,0226

64,7

Etanol

0,0223

78,15

Etar

0,0170

34,6

Na dodiru dve te~ne faze, koje se ne me{aju ili se delimi~no

me{aju, javlja se tzv.

grani~ni sloj

u kome se nalaze molekuli obe faze,

ali u druga~ijem polo`aju u pore|enju sa molekulima u ~istim faza-

ma. Napon koji se javlja u ovom grani~nom sloju posledica je me-

|udejstva prisutnih molekula, pa se naziva

me|upovr{inski napon

ili

me|ufazni napon

(raniji naziv

dodirni napon

). Ovaj napon je

manji od povr{inskog napona, jer su adhezione sile u grani~nom

sloju izme|u dve te~nosti ve}e od sila koje se javljaju izme|u mo-

lekula te~ne i gasovite faze.

Iz koeficijenta povr{inskog napona mo`e se izra~unati veli~ina

koju je Sugden (Sugden) nazvao

parahor te~nosti P

gde je:

M – molarna masa analizirane te~nosti

– koeficijent povr{inskog napona te~nosti

– gustina te~nosti

– gustina pare.

Na ni`im temperaturama gustina pare je mnogo manja od gu-

stine te~nosti, pa se mo`e zanemariti. Izraz za parahor dobija jed-

nostavniji oblik:

Medenica / Male{ev

Tablica 1.

Povr{inski napon i ta~ka klju~anja

pojedinih te~nosti

P = M

–

(1)

P = M

(2)

Parahor ima dimenzije molarne zapremine pomno`ene sa ~etvr-

tim korenom povr{inskog napona (m

mol

-1

-¼

). To je aditiv-

na i konstitutivna veli~ina, {to zna~i da zavisi od vrste, broja i na~ina

vezivanja atoma u molekulu. Mo`e se izra~unati sabiranjem vred-

nosti parahora atoma i veza u molekulu (tablica 2 u Prilogu).

U farmaceutskim istra`ivanjima odre|ivanje povr{inskog napo-

na je od zna~aja za uspostavljanje veze izme|u povr{inske aktivnosti

leka i njegovog biohemijskog i farmakolo{kog dejstva. Tako|e, mo`e

se odrediti i ~isto}a te~nosti, jer eventualno prisutne ne~isto}e me-

njaju vrednost koeficijenta povr{inskog napona.

odre|ivanje povr{inskog napona

postoje razli~ite metode, u

zavisnosti od ta~nosti koja se `eli posti}i, od koli~ine uzorka sa ko-

jim se raspola`e i od jednostavnosti rada.

Metoda merenja mase kapi podrazumeva odre|ivanje broja kapi

koje isteknu iz odre|ene zapremine i merenja njihove mase. U tu

svrhu koristi se Traubeov (Traube) stalagmometar. To je relativna

metoda, jer se povr{inski napon analizirane te~nosti upore|uje sa

povr{inskim naponom standardnog rastvora. Zato je potrebno pret-

hodno kalibrisati stalagmometar sa standardom (npr. vodom).

Traubeov stalagmometar (slika 2) je staklena cev sa pro{irenjem i

kapilarom na donjem kraju, koja se zavr{ava ravnom povr{inom.

Kap te~nosti koja se obrazuje na donjem delu kapilare (prilikom

slobodnog isticanja te~nosti u obliku kapi) otkida se u trenutku ka-

da njena masa savlada povr{inski napon. Ukoliko je povr{inski na-

pon ve}i bi}e i masa kapi ve}a. To zna~i da }e se iz iste zapremine ob-

razovati manji broj kapi. Masa kapi data je slede}im izrazom:

gde je:

m – masa kapi

V – zapremina te~nosti

– gustina te~nosti

n – broj kapi u zapremini V.

Eksperimentalna fizi~ka hemija

Slika 2.

Traubeov stalagmometar

m =

V .

(3)

Metoda merenja mase kapi

Metoda kapilarne cevi (

kapilarna elevacija

) je najpouzdanija meto-

da za odre|ivanje povr{inskog napona. Zasniva se na merenju visine

podizanja te~nosti u kapilarnoj cevi poznatog pre~nika (slika 3).

U kapilari te~nost koja kvasi zidove suda, stvara pritisak usled

delovanja povr{inskog napona te~nosti, koji je prikazan Laplasovom

(Laplace) jedna~inom:

gde je:

– povr{inski napon te~nosti

r – polupre~nik kapilare.

Usled kapilarnih pojava, odnosno adhezionih sila koje slabe pri-

tisak P

dolazi do podizanja te~nosti u kapilari do izvesne visine,

usled pritiska koji vlada u masi te~nosti zbog povr{inskog napona.

Hidrostati~ki pritisak stuba te~nosti koji se stvara u kapilarnoj cevi,

u ta~ki B, jednak je:

gde je:

– gustina te~nosti

g – ubrzanje Zemljine te`e

h – visina stuba te~nosti u kapilarnoj cevi.

Te~nost u kapilari zaustavi}e se na nekoj visini

kada se us-

postavi ravnote`a izme|u pritisaka

iz koje se mo`e, merenjem visine stuba te~nosti

iznad nivoa te~-

nosti, izra~unati povr{inski napon te~nosti:

Vrednost

je poznata veli~ina za analiziranu te~nost na temperaturi

merenja. Vrednost

je poznata za datu kapilaru ili se mo`e odrediti

kori{}enjem te~nosti poznatih

Eksperimentalna fizi~ka hemija

Slika 3.

Kapilarni efekat

P – pritisak usled povr{inskog

napona

h – visina stuba te~nosti u kapilari

izme|u ta~aka A i B

(8)

. g . h =

(10)

r .

. g . h

(11)

. g . h

(9)

Metoda kapilarne cevi

Me|upovr{inski napon

(koji se javlja na granici dve te~ne faze koje

se ne me{aju ili se delimi~no me{aju) odre|uje se istim metodama

kao i povr{inski napon. Metodom kapilarne cevi, (slika 4) izvodi se

tako {to se te~nost A manje gustine sipa u pro{ireni deo suda koji se

zavr{ava kapilarom polupre~nika

. Kapilara se uranja u te~nost B

ve}e gustine. Pomeranjem suda A gore-dole podesi se da dodirne

povr{ine te~nosti u sudu A i te~nosti u sudu B budu na istom nivou i

izmeri visina stuba te~nosti

. Tada se me|upovr{inski napon izra-

~unava iz jedna~ine (11) i poznate vrednosti gustine

za te~nost A.

Medenica / Male{ev

Slika 4.

Odre|ivanje me|upovr{inskog napona

A – sud sa te~no{}u manje gustine

B – sud sa te~no{}u ve}e gustine

h – visina stuba te~nosti

oznake stalagmometra i stegnuti {tipaljku da te~nost ne isti~e. Kali-

braciju stalagmometra uraditi sa destilovanom vodom prema pos-

tupku datom za odre|ivanje zapremine jedne kapi i za odre|ivanje

broja kapi u pro{irenom delu stalagmometra.

b) Odre|ivanje zapremine jedne kapi

Menisk te~nosti izjedna~iti sa prvom crtom na gornjem, graduisa-

nom delu stalagmometra. Pa`ljivo ispustiti jednu kap i zapisati koli-

ko podeoka zauzima.

c) Odre|ivanje broja kapi u pro{irenom delu stalagmometra

Povu}i te~nost u gornji, graduisani deo stalagmometra. Zapisati po-

deok iznad pro{irenja na kome se nalazi menisk te~nosti. Obrisati

kap sa donjeg dela stalagmometra i podesiti da te~nost isti~e u kapi-

ma. Brojati kapi, a brojanje zavr{iti kada te~nost u|e u donji, gradui-

sani deo stalagmometra i zapisati broj podeoka. Zbir podeoka iznad

i ispod pro{irenja podeliti brojem podeoka koji zauzima jedna kap.

Ovaj koli~nik, odnosno vi{ak kapi, izra~unat sa ta~no{}u jednog de-

cimalnog mesta, oduzeti od ukupnog broja kapi. Dobijena razlika

predstavlja broj kapi

u pro{irenom delu stalagmometra. Broj kapi

odrediti tri puta za destilovanu vodu, a zatim izra~unati srednju

vrednost.

Postupak

Stalagmometar isprati sa malo etanola i osu{iti na vakuumu. Odre-

diti broj kapi

za analiziranu te~nost na isti na~in kao za destilo-

vanu vodu.

Iz eksperimentalno dobijenih srednjih vrednosti broja kapi, da-

tih vrednosti za gustinu i koeficijent povr{inskog napona vode (tab-

lica 3 u Prilogu) i gustine analizirane te~nosti na radnoj temperatu-

ri, izra~unati koeficijent povr{inskog napona i parahor.

Rezultate prikazati tabelarno.

Medenica / Male{ev

Eksperimentalna fizi~ka hemija

– broj podeoka koje zauzima jedna kap

– broj podeoka iznad pro{irenja

– broj podeoka ispod pro{irenja

– ukupan broj kapi

– broj kapi u vi{ku zapremine

[

(

) /

]

– broj kapi u pro{irenom delu stalagmometra (

) (n =

–

)

t = ........ °C

M = ...... kg mol

-1

Tabela 1.

Odre|ivanje broja kapi u stalagmometru

Voda

Analizirana te~nost

uzorak

broj kapi < n >

voda

te~nost

(kg m

-3

)

(N m

-1

)

Tabela 2.

Povr{inski napon

REZULTATI

Pritisak pare rastvara~a iznad ~istog rastvara~a ve}i je od pritiska pa-

re rastvara~a iznad rastvora, koji sadr`i neisparljivu rastvorenu sup-

stanciju (rastvorak), pod uslovom da su pritisci mereni na istoj tem-

peraturi.

Na osnovu ovih saznanja Raul (Raoult) je dao zakon, koji glasi:

Relativno sni`enje pritiska pare iznad rastvora jednako je odnosu broja

molova rastvorka i ukupnog broja molova rastvara~a i rastvorka

Matemati~ka formulacija ovog zakona data je jedna~inom:

gde je:

0 – pritisak pare iznad rastvara~a

– pritisak pare iznad rastvora

– broj molova rastvara~a

– broj molova rastvorka

/(n

+ n

) – molski udeo ili molska frakcija rastvorka.

Iz jedna~ine (1) vidi se da je pritisak pare iznad rastvora

manji,

kada je

, odnosno koncentracija rastvora ve}a. Raulov zakon va`i

za razbla`ene rastvore, a sa pove}anjem koncentracije raste i odstu-

panje od ovog zakona.

Posledica smanjenog pritiska pare iznad rastvora je povi{enje tem-

perature klju~anja i sni`enje temperature mr`njenja rastvora (ta~ni-

je rastvara~a u rastvoru) u odnosu na ~ist rastvara~, {to je prikazano

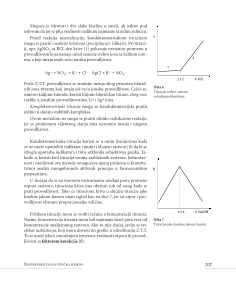
na dijagramu (slika 1).

Eksperimentalna fizi~ka hemija

KRIOSKOPIJA

(gr~ki

krios

– mraz i

skopein

– posmatrati)

Teorijski princip

– P

– n

(1)

Pritisak pare vode (P

) raste sa pove}anjem temperature, sve dok

se na t = 100°C ne izjedna~i sa pritiskom gasne faze, odnosno vaz-

duhom (ta~ka A), koji iznosi 101.325 Pa (jednu atmosferu, odnosno

760 mm `ivinog stuba). Na toj temperaturi voda po~inje da klju~a,

{to zna~i da je uspostavljena ravnote`a izme|u te~ne i gasovite faze.

Po{to je pritisak pare vode (P) iznad rastvora na t = 100°C (ta~ka D)

manji, potrebno je pove}ati temperaturu da bi se pritisak pare izjed-

na~io sa atmosferskim pritiskom (ta~ka C) kada rastvor po~inje da

klju~a. Razlika izme|u temperatura klju~anja vode i rastvora oz-

na~ena je sa

∆

klj

Pritisak pare iznad vode se smanjuje sa sni`enjem temperature i

kad se izjedna~i sa pritiskom pare iznad leda (ta~ka B), koji iznosi

610,6 Pa na t = 0°C, voda po~inje da kristali{e. Time se uspostavlja

ravnote`a izme|u ~vrste i te~ne faze, dok se sva voda ne pretvori u

led. Vidi se da je odgovaraju}i pritisak pare iznad rastvora (ta~ka E)

manji zbog ~ega je rastvor stabilniji od vode, pa ne podle`e kristali-

zaciji. Na temperaturama ispod 0°C postoji samo led, za koji kriva

napona pare (BF) ima strmiji tok od krive napona pare vode (AB) i

krive napona pare iznad rastvora (CF), jer su promene napona pare

sa promenom temperature ve}e iznad leda nego iznad vode i vo-

Medenica / Male{ev

Slliik

a 1

1..

Krive P = f(t°C) za vodu

i vodeni rastvor

Iz jedna~ina (4) i (6) dobija se izraz za izra~unavanje molarne mase

rastvorka krioskopskom metodom:

Jedna~ina (7) va`i za razbla`ene rastvore neelektrolita, kao i za

rastvore u kojima kristali{e samo rastvara~, a ne i rastvorak. To se

posti`e izborom rastvara~a, ~ija je ta~ka mr`njenja mnogo ve}a u

odnosu na rastvorak, ~ija se molarna masa odre|uje. U suprotnom

ne}e va`iti Raulov zakon (1), prema kome para iznad rastvora poti~e

samo od rastvara~a, dok se rastvorak smatra neisparljivim.

Povi{enje ta~ke klju~anja i sni`enje ta~ke mr`njenja spadaju u

koligativne osobine

te~nih rastvora. To su osobine koje zavise od

broja ~estica rastvorka prisutnih u odre|enoj zapremini rastvara~a,

a ne zavise od prirode ~estica, njihove veli~ine, oblika, hemijskog

sastava i naelektrisanja.

Na|eno je da su sni`enja ta~ke mr`njenja i povi{enja ta~ke klju-

~anja rastvora slabih i jakih elektrolita ve}a u odnosu na rastvore ne-

elektrolita iste molalne koncentracije, {to se obja{njava pove}anjem

broja ~estica rastvorka u rastvorima elektrolita usled disocijacije

molekula. Zbog odstupanja rastvora elektrolita od Raulovog za-

kona, Van Hof (van’t Hoff ) je uveo korekcioni broj

, tako da se jed-

na~ina (2) mo`e primeniti i na rastvore elektrolita:

Van Hofov broj

se defini{e kao odnos broja ~estica u rastvoru elek-

trolita i broja ~estica u rastvoru neelektrolita, pri istim molalnim

koncentracijama ovih rastvora. Deljenjem jedna~ine (8) sa jedna~i-

nom (2), dobija se jedna~ina za izra~unavanje broja

gde su

∆

t’ i

∆

t sni`enja ta~ke mr`njenja rastvora elektrolita, odnosno

neelektrolita istih molalnih koncentracija.

Medenica / Male{ev

(7)

M = K

a .

1000

b .

∆

(9)

i =

∆

’

∆

t’ = k . c . i

(8)

Na primer,

∆

t’ razbla`enog rastvora jakog elektrolita NaCl, koji

disosuje na Na

i Cl

–

jone, dva puta je ve}e od

∆

t rastvora neelek-

trolita iste koncentracije, pa iz jedna~ine (9) sledi da je i

NaCl

= 2. Za

izra~unavanje molarne mase elektrolita koristi se jedna~ina (7) u

slede}em obliku:

Ebulioskopska metoda

se zasniva na merenju povi{enja ta~ke klju-

~anja rastvora u odnosu na rastvara~. Za odre|ivanje molarne mase

ovom metodom primenjuju se sve jedna~ine date kod krioskopske

metode, osim {to se krioskopska zamenjuje ebulioskopskom kon-

stantom

. Ebulioskopska metoda se retko koristi za odre|ivanje

molarne mase, jer je odre|ivanje sni`enja ta~ke mr`njenja mnogo

jednostavnije. Pored toga, vrednosti krioskopskih konstanti rast-

vara~a (K

= 1,86) ve}e su od ebulioskopskih (E

= 0,52).

Zbog toga su osetljivost i ta~nost odre|ivanja molarne mase krio-

skopskom metodom ve}i, jer ve}oj vrednosti konstante rastvara~a

odgovara ve}a vrednost

∆

t, {to se vidi iz jedna~ine (7).

Eksperimentalna fizi~ka hemija

(10)

M = K

. i

a .

1000

b .

∆

Aparatura i hemikalije

Aparat za merenje sni`enja ta~ke mr`njenja po Bekmanu

(Beckmann) (slika 2)

Termometar

Lupa

Hronometar

Uzorak za odre|ivanje molarne mase

Natrijum-hlorid

Led

ostupak

Odmeriti na analiti~koj vagi oko 0,4 g supstancije, ~ija se molarna

masa odre|uje, sa ta~no{}u 1×10

-4

Pripremiti aparaturu za merenje sni`enja ta~ke mr`njenja prema

slici 2. U posudu za hla|enje sipati sme{u za hla|enje koju ~ine isit-

njen led i natrijum-hlorid. U sme{u uroniti termometar. Tempera-

tura sme{e treba da se kre}e u intervalu od –3 do –5°C, koja se posti-

`e odre|enom koli~inom natrijum-hlorida u sme{i.

Promene temperature pratiti na Bekmanovom termometru. To je

`ivin termometar koji ima dva rezervoara povezana kapilarom. Ovim

termometrom vr{e se relativna merenja, {to zna~i da se ne mo`e od-

rediti temperatura, ve} samo temperaturska razlika. Skala je gradui-

sana u opsegu od 5 do 6 stepeni. Za o~itavanje desetih i stotih delova

stepena koristiti malu lupu, koja je obi~no pri~vr{}ena za termometar.

Pre svakog merenja potrebno je doterati Bekmanov termometar. To

zna~i da `ivu treba tako rasporediti izme|u dva rezervoara, da se tem-

peratura mr`njenja rastvora na|e na donjoj polovini skale. Time je

omogu}eno pra}enje promene temperature u odre|enim vremen-

skim intervalima i grafi~ko prikazivanje krivih hla|enja.

Pipetom odmeriti 20 mL destilovane vode i preneti je u epruvetu

A. Zatim dodati prethodno odmerenu masu supstancije, vode}i ra-

~una da se sva koli~ina rastvori i da nema ostataka supstancije na zidu

epruvete. Spustiti Bekmanov termometar i me{alicu tako da termo-

metar skoro dodiruje dno epruvete. Vodu me{ati ravnomerno po-

meranjem me{alice gore-dole i pratiti promenu temperature na ter-

mometru. Hronometar uklju~iti kada `ivin konac padne na skalu i

o~itavati temperaturu svakih pola minuta. Temperatura }e stalno

opadati i od momenta kada rastvor po~ne da kristali{e, termometar

}e pokazivati konstantnu vrednost sve dok sva koli~ina rastvora ne

Eksperimentalna fizi~ka hemija

iskristali{e. Na ovaj na~in odre|ena je temperatura mr`njenja rast-

vora (t

Epruvetu A izvaditi zajedno sa Bekmanovim termometrom i

me{alicom i zagrevati u ruci, dok se svi kristali ne istope. Postupak

merenja temperature mr`njenja rastvora ponoviti jo{ jednom.

Epruvetu A, uronjene delove termometra i me{alice oprati od

rastvora obi~nom, pa zatim destilovanom vodom i sipati pribli`no

20 mL destilovane vode. Ponovo spustiti termometar i me{alicu i

odrediti temperaturu mr`njenja vode (t

) dva puta.

^esto se de{ava da se temperatura rastvara~a, odnosno rastvora

spusti ispod temperature mr`njenja neposredno pre mr`njenja. Ova

pojava naziva se

prehla|enje

. Kada prehla|ena te~nost po~ne da

kristali{e, temperatura se naglo popne do temperature mr`njenja i

ostaje na toj temperaturi sve dok sva koli~ina ne iskristali{e.

U istom koordinativnom sistemu prikazati krive hla|enja za

rastvara~ i rastvor i odrediti vrednost

∆

t (

∆

t = t

– t

), a zatim izra-

~unati molarnu masu. Vrednost za krioskopsku konstantu uzeti iz

tablice 4 u Prilogu.

Rezultate prikazati tabelarno i grafi~ki.

Medenica / Male{ev

(3)

Termi~ke

osobine rastvora

KALORIMETRIJA

Odre|ivanje toplote rastvaranja

Svaka fizi~ka promena (rastvaranje, promena agregatnog stanja, pre-

laz jedne kristalne modifikacije u drugu) ili hemijska reakcija (sjed-

injavanje, neutralizacija, sagorevanje) pra}ena je energetskim prom-

enama sistema, u kojima se ovi procesi de{avaju. Koli~ina toplote

koju neki sistem primi ili otpusti pri nekom procesu, naziva se

to-

plotni efekat

. Kad raste temperatura sistema, u kome se proces od-

vija, zna~i da sistem odaje deo toplote okolini. Takav proces je

egzo-

terman

. Naprotiv, kad temperatura u toku procesa opada, zna~i da

sistem prima toplotu od okoline, pa je proces

endoterman

Metoda za odre|ivanje toplotnog efekta fizi~kih i hemijskih pro-

cesa naziva se

kalorimetrija

, a ure|aj za merenje toplotnog efekta

kalorimetar

. To je izolovan sistem, koji ne razmenjuje toplotu sa

okolinom, ~ime se posti`e ta~no merenje toplotnog efekta. Savr{eno

izolovan, odnosno adijabatski sistem ne mo`e se napraviti, pa je po-

trebno da se proces brzo zavr{i. Pored toga, temperaturska promena,

Eksperimentalna fizi~ka hemija

RIIM

RIIJJA

(latinski

calor

– toplota i gr~ki

metron

– mera)

Teorijski princip

Slliik

a 1

1..

Kalorimetar sa vodom

A – spolja{nja metalna posuda

B – za{titna posuda

C – staklena ~a{a

D – Bekmanov termometar

E – lupa

F – me{alica

G – termometar termostata

to iz jedna~ina (1) i (2) sledi izraz za izra~unavanje molarne toplote

rastvaranja:

Toplotni kapacitet

defini{e se kao koli~ina toplote, koju je

potrebno dovesti jednom sistemu, da mu se temperatura povisi za

jedan stepen. U zavisnosti od koli~ine sistema kome se dovodi

toplota, postoji vi{e definicija toplotnog kapaciteta.

Specifi~ni toplotni kapacitet

ili

specifi~na toplota c

odnosi se

na jedan gram supstancije. Po{to toplotni kapacitet zavisi od tem-

perature, na kojoj sistem prima toplotu, posebno je definisana

specifi~na toplota vode c

. To je koli~ina toplote potrebna da se

jedan gram vode zagreje od 14,5°C do 15,5°C. Ona iznosi:

Toplotni kapacitet sistema koji sadr`i

grama supstancije, dat je

jedna~inom:

Ukupni toplotni kapacitet kalorimetra

predstavlja zbir toplot-

nog kapaciteta ~vrstih delova kalorimetra, koji su primili toplotu

, i toplotnog kapaciteta vode

Prema jedna~ini (5),

se izra~unava iz izraza:

gde se pod

podrazumevaju mase ~a{e i uronjenih delova ter-

mometra i me{alice, a

odgovaraju}e specifi~ne toplote.

va`i:

gde je:

– masa vode

– specifi~na toplota vode.

Eksperimentalna fizi~ka hemija

Q =

∆

cor

(3)

= 1 cal = 4,186 KJ kg

-1

(4)

C = m . c

(5)

C = C

+ C

(6)

= m

. c

(7)

(8)

Po{to je

poznato, a podaci za

, u zavisnosti od temperature,

nalaze se u termodinami~kim tablicama (tablica 5 u Prilogu), to je

za izra~unavanje molarne toplote rastvaranja potrebno znati toplot-

ni kapacitet ~vrstih delova kalorimetra

Odre|ivanje toplotnog kapaciteta ~vrstih delova kalorimetra

Za odre|ivanje toplotnog kapaciteta ~vrstih delova kalorimetra

pored drugih metoda, koristi se i tzv.

metoda me{anja

. Toplota koju

neko telo primi ili preda jednaka je proizvodu toplotnog kapaciteta

tela i temperaturske razlike:

Koli~ina toplote koju je topla voda predala hladnoj vodi i ~vrstim

delovima kalorimetra bi}e:

gde je:

–

masa tople vode

–

temperatura tople vode

–

temperatura sme{e.

Koli~ina toplote koju su primili hladna voda i ~vrsti delovi kalo-

rimetra iznosi:

gde je:

–

masa hladne vode

–

temperatura hladne vode.

Na temperaturi sme{e

izvr{ena je potpuna razmena toplote.

Mo`e se napisati da je:

Medenica / Male{ev

= m

. c

– t)

(10)

= Q

Q = C .

∆

(9)

= m

. c

(t – t

) + C

(t – t

)

(11)

(12)

Medenica / Male{ev

Aparatura i hemikalije

Kalorimetar (slika 1, strana 39)

Analizirana supstancija

Destilovana voda

Postupak

Odre|ivanje toplotnog kapaciteta kalorimetra vr{i se tako {to se

menzurom odmeri 100 g vode na sobnoj temperaturi, sa ta~no iz-

merenom vredno{}u i prenese u kalorimetar. Zatim uroniti termo-

metar sa opsegom od 50°C i uklju~iti me{alicu. Kontrolisati tempera-

turu svakih pola minuta. Kad se temperatura ustali, naglo sipati 100 g

vode sa ta~no izmerenom temperaturom u intervalu 50–60°C. Pra-

titi porast temperature i odrediti najvi{u temperaturu sme{e hladne

i tople vode, koja zatim polako opada zbog izmene toplote sa okoli-

nom.

Odmeriti 4–6 g supstancije sa ta~no{}u ± 1×10

-3

g (

). U kalori-

metarsku ~a{u sipati 300 mL destilovane vode (

), uroniti Bekma-

nov termometar i uklju~iti me{alicu.

Odmah po~eti sa ~itanjem temperature svakih pola minuta, be-

le`e}i vrednosti prema ta~nosti skale. Posle 10–15 ~itanja, kad se

temperatura ustali, tj. kada razlike izme|u dva uzastopna ~itanja po-

stanu nemerljive, zavr{ena je

po~etna perioda

Podi}i poklopac, brzo ubaciti odmerenu masu analizirane sup-

stancije u ~a{u, staviti poklopac i dalje ~itati temperaturu svakih po-

la minuta u kontinuitetu sa po~etnom periodom. Nagla promena

temperature je posledica toplotnog efekta rastvaranja. Da ne bi do-

{lo do ve}e izmene toplote sa okolinom, rastvaranje mora biti brzo.

Ovo je

glavna perioda

i zbog nagle promene temperature prva ~ita-

nja se ne mogu izvesti sa ta~no{}u kao kod po~etne periode.

URADITE SAMOSTALNO ...

Odre|ivanje

toplote

rastvaranja

Zadatak eksperimenta

Metodom me{anja odrediti toplotni kapacitet ~vrstih delova ka-

lorimetra.

Odrediti molarnu toplotu rastvaranja analizirane supstancije.

Eksperimentalna fizi~ka hemija

zavr{noj periodi

temperatura se postepeno menja (zbog iz-

mene toplote sa okolinom). ^itanja temperature treba zavr{iti kao i

kod po~etne periode.

Rezultate prikazati tabelarno i grafi~ki.

Grafi~ki prikazati promenu temperature u funkciji vremena i

odrediti

∆

cor

na slede}i na~in: povu}i prave kroz najve}i broj ta~aka

po~etne periode, a zatim kroz najve}i broj ta~aka zavr{ne periode.

Paralelno ordinati povu}i pravu koja se~e glavnu periodu, tako da

dve povr{ine P

i P

budu pribli`no jednake, kao {to pokazuje slika 2.

Rastojanje izme|u ta~aka A i B predstavlja korigovanu temperatur-

sku razliku. Ukupni toplotni kapacitet C izra~unati iz jedna~ina (6),

(8) i (14), a zatim molarnu toplotu rastvaranja Q iz jedna~ine (3).

Slliik

a 2

2..

Promena temperature sa vremenom

1 – po~etna

2 – glavna

3 – zavr{na perioda

(4)

Osobine

molekula

REFRAKTOMETRIJA

Odre|ivanje molarne

refrakcije rastvora

POLARIMETRIJA

Odre|ivanje koncentracije

rastvora saharoze

Brzina svetlosti je najve}a u vakuumu, a menja se u zavisnosti od gu-

stine i prirode sredine kroz koju prolazi. Odnos izme|u brzine svet-

losti u vakuumu

i nekoj sredini

je konstanta za datu sredinu i

naziva se

apsolutni indeks prelamanja

Odnos izme|u brzina svetlosti u bilo kojim dvema sredinama

naziva se

relativni indeks prelamanja

i predstavlja konstantu za obe sredine. Promena brzine svetlosnog

zraka, pri njegovom prelazu iz jedne u drugu sredinu, manifestuje se

promenom pravca kretanja (slika 1).

Ako je sredina (2) gu{}a od sredine (1), zrak se prelama ka nor-

mali, tako da je ugao i

uvek ve}i od ugla i

. Odnos indeksa prela-

manja za ove dve sredine dat je izrazom:

Odatle je:

Veli~ina

2,1

predstavlja relativni indeks prelamanja ili, kra}e,

in-

deks prelamanja

ili

indeks refrakcije

i odgovara veli~ini datoj u

jedna~ini (2). Indeks prelamanja zavisi od prirode i jedne i druge

sredine, talasne du`ine svetlosti (va`i samo za monohromatsku svet-

lost) i temperature. Zbog toga je potrebno naglasiti uslove pod koji-

ma je izmeren indeks prelamanja. Naj~e{}e su merenja vr{ena ko-

riste}i `utu natrijumovu D liniju, ~ija talasna du`ina

iznosi 589,3

nm i na sobnoj temperaturi od 20°C ili 25°C. Tako odre|en indeks

prelamanja ozna~ava se simbolima n

ili n

Eksperimentalna fizi~ka hemija

REFRAKTOMETRIJA

(latinski

refractus

– prelomljen)

Teorijski princip

Slika 1.

Prelamanje svetlosnog zraka

(1)

aps

(2)

rel

(4)

sin i

= n

(3)

. sin i

= n

. sin i

veza koje postoje u molekulu). Zahvaljuju}i ovim osobinama, mo-

larna refrakcija se koristi za odre|ivanje strukture organskih jed-

injenja. Na primer, u homologom nizu alkohola svaka CH

grupa

pove}ava vrednost R

za oko 4,634. Aditivnost i konstitutivnost

molarne refrakcije ogledaju se u dobrom slaganju izra~unate R

vrednosti iz izmerenih indeksa refrakcije (jedna~ina 6) i izra~unate

vrednosti iz atomskih refrakcija. Na primer, eksperimentalna R

vrednost za benzol iznosi 26,15, a izra~unata 26,31, pod uslovom da

su merenja indeksa prelamanja izvr{ena koriste}i natrijumovu D

liniju (n

Pomo}u molarne refrakcije mogu se identifikovati izomerni ob-

lici nekog jedinjenja ili odrediti koji tautomerni oblik dominira u je-

dinjenju.

Po{to indeks prelamanja zavisi od talasne du`ine propu{tene

svetlosti i veli~ine koje su izvedene iz indeksa prelamanja, specifi~na

i molarna refrakcija tako|e zavise od talasne du`ine. Razlika speci-

fi~nih refrakcija na dve talasne du`ine, r

– r

, naziva se

specifi~na

disperzija

, a razlika molarnih refrakcija, R

– R

molarna dis-

perzija

. Obe disperzije imaju svojstvo aditivnosti i koriste se pri

odre|ivanju tipa veze atoma u molekulu.

Aditivne i konstitutivne osobine molarne refrakcije mogu se ko-

ristiti za odre|ivanje sastava sme{e. Molarna refrakcija sme{e dve

te~nosti data je izrazom:

gde je:

1,2

– molarna refrakcija sme{e

n – indeks prelamanja sme{e

i x

– molski udeo komponente 1 i 2

i M

– molarna masa komponente 1 i 2.

Utvr|eno je da veli~ina R

1,2

predstavlja zbir doprinosa pojedi-

na~nih konstituenata:

gde su R

i R

molarne refrakcije komponenata 1 i 2.

Eksperimentalna fizi~ka hemija

1,2

– 1

+ 2

+ x

(7)

1,2

= x

+ x

(8)

Iz izmerenih vrednosti indeksa prelamanja sme{e, indeksa prela-

manja pojedina~nih komponenata, gustine sme{e, gustine pojedi-

na~nih komponenata i molarnih masa komponenata, prvo se mogu

izra~unati molarne refrakcije komponenata iz jedna~ine (6), a po-

tom i molski udeli komponenata, odnosno sastav sme{e, pomo}u

jedna~ina (7) i (8). Ove jedna~ine va`e pod uslovom da zapremina

sme{e predstavlja aditivnu vrednost zapremina komponenata. U

tom slu~aju, za indeks prelamanja sme{e va`i izraz:

gde su:

i n

– indeksi prelamanja te~nosti 1 i 2

i V

– zapremine te~nosti 1 i 2.

Indeks prelamanja odre|uje se pomo}u opti~kog instrumenta

koji se naziva

refraktometar

. Najprostiji tipovi refraktometara su

Abeov

(Abbe),

Pulfrihov

(Pulfrich) i

imerzioni refraktometar

. Odre-

|ivanje indeksa prelamanja

neke te~nosti zasniva se na merenju

grani~nog ugla i

pri prelasku svetlosti iz ispitivane te~nosti u stak-

lenu prizmu poznatog indeksa prelamanja

(slika 2). Grani~ni

ugao

je najve}i ugao pod kojim se mo`e prelomiti zrak kad pre-

lazi iz jedne sredine u drugu. Da bi se to postiglo, svetlost mora pa-

dati na dodirnu povr{inu dve sredine skoro paralelno, odnosno pod

uglom od 90° u odnosu na normalu. [rafirani deo predstavlja ne-

osvetljeni deo prizme. Ako bi se svetlost kretala suprotnim smerom,

odnosno prelazila iz prizme u te~nost, zraci koji padaju pod uglom

ve}im od grani~nog ne bi mogli pre}i u te~nost, ve} bi se odbijali od

povr{ine prizme i ponovo u nju vratili, {to je poznato pod imenom

totalna refleksija

Kada se jedna~ina (3) za prelamanje svetlosti primeni na sliku 2,

va`i:

Po{to je sin 90° = 1, bi}e:

Medenica / Male{ev

n =

+ V

(9)

Slika 2.

Put grani~nog zraka

(10)

n .

sin 90°

= N .

sin

(11)

n = N .

sin

Izvor svetlosti

mo`e biti bela svetlost, sun~eva ili obi~na vol-

framova sijalica. Svetlosni zraci reflektovani sa ogledala

prolaze

kroz prizmu

, ~ija je gornja povr{ina grubo izbru{ena. Ova povr-

{ina slu`i kao izvor svetlosnih zraka koji prolaze kroz sloj te~nosti

debljine 0,1 mm i prelamaju se na poliranoj povr{ini prizme

Maksimalan ugao pod kojim se zrak prelama u prizmi

predstavlja

grani~ni ugao

, koji stvara granicu izme|u levog tamnog dela, i de-

snog svetlog dela vidnog polja

. Na granici prizma

– vazduh, zraci

se ponovo prelamaju i prolaze kroz teleskop

u kome se nalaze roti-

raju}e Ami}ijeve (Amici) prizme

, koje propu{taju monohro-

matsku svetlost. Po prolasku kroz prizme, svetlost pada na vidno

polje

sa ukr{tenim kon~anicama

Odre|ivanje indeksa prelamanja te~nosti vr{i se tako {to se

prizme Q i P obr}u do pojave grani~nog ugla, odnosno granice iz-

me|u tamnog i svetlog polja na vidnom polju L. Ako svetlost nije

monohromatska, ova granica nije o{tra i sadr`i spektar boja. Zbog

toga se vr{i obrtanje Ami}ijevih prizmi, koje pod izvesnim uglom

propu{taju samo natrijumovu D liniju od 589,3 nm. Propu{tanje

monohromatske svetlosti manifestuje se pojavom o{tre granice iz-

me|u tamnog i svetlog dela vidnog polja. Pomo}u rotiraju}ih priz-

mi Q i P, grani~na linija se ponovo pomeri, tako da se dovede u ta~ku

preseka kon~anica, a zatim se na skali S direktno pro~ita indeks pre-

lamanja te~nosti.

Medenica / Male{ev

Aparatura i hemikalije

Abeov refraktometar (slika 4)

Analizirani rastvor

Priprema Abeovog refraktometra

Odvrnuti zavrtanj koji spaja prizme, odvojiti donju prizmu Q od

gornje P i »lenz« papirom (papir za brisanje opti~kih povr{ina) ili

vatom natopljenom etanolom, obrisati obe prizme. Sa~ekati da se

prizme osu{e isparavanjem etanola. Pipetom naneti analiziranu te~-

nost na celu povr{inu donje prizme Q, ne dodiruju}i prizmu pipe-

tom. Podi}i donju prizmu i pri~vrstiti je zavrtnjem za gornju.

Merenje indeksa prelamanja

Zavrtanj na levoj strani refraktometra okretati sve dok se na vidnom

polju desnog okulara ne pojavi granica tamno-svetlo. Zavrtnjem na

desnoj strani instrumenta izo{triti granicu. Ponovo zavrtnjem sa le-

ve strane prizme podesiti granicu {to je mogu}e preciznije na presek

kon~anica (dveju unakrsnih crnih linija). Indeks prelamanja o~itava

se na levom okularu (leva skala), sa ta~no{}u koja karakteri{e instru-

ment (1×10

-4

Eksperimentalna fizi~ka hemija

URADITE SAMOSTALNO ...

Odre|ivanje molarne

refrakcije rastvora

Zadatak eksperimenta

Izmeriti deset puta vrednosti indeksa prelamanja analiziranog

uzorka na sobnoj temperaturi.

Odbaciti one vrednosti indeksa prelamanja koje najvi{e

odstupaju i izra~unati srednju vrednost <n> (poglavlje

Statisti~ka

obrada rezultata

u Prilogu). Iz poznate vrednosti molarne mase i

gustine izra~unati molarnu refrakciju Rm (eksp.).

Statisti~kom obradom dobijenih rezultata, metodom

»Studentove t-raspodele«, izra~unati ta~nost odre|ivanja indeksa

prelamanja.

Na osnovu strukturne formule ispitivanog jedinjenja izra~unati

molarnu refakciju Rm (izra~.).

Na osnovu poznate strukturne formule i tabli~nih vrednosti re-

frakcija atoma i veza (tablica 6 u Prilogu) izra~unati molarnu refrak-

ciju

(izra~unato)

Na osnovu razlike

∆

Rm = Rm

– Rm

i tabli~nih vrednosti mo-

larnih refrakcija veza, odrediti broj dvostrukih veza.

Rezultate prikazati tabelarno.

Eksperimentalna fizi~ka hemija

Medenica / Male{ev

Merenje

Indeks prelamanja

(n)

∆

< n >

<n>

M (kg mol

-1

)

(kg m

-3

)

Rm (m

mol

-1

)

eksperimentalno

izra~unato

∆

Rm (m

mol

-1

)

BROJ

(=)

VEZA

ella

a 1

1..

Rezultati merenja

ella

a 2

2..

Rezultati za molarnu refrakciju

REZULTATI

Jedinjenje____________________

Transverzalni talas

nastaje kad ~estice osciluju u pravcu koji je nor-

malan na pravac prostiranja talasa. Osobine talasnog kretanja u me-

hanici mogu se preneti na svetlost, koja predstavlja talasno kretanje

elektromagnetske prirode.

Svetlosni talas

se sastoji od dva spregnu-

ta talasa, elektri~nog i magnetskog, koji se prostiru u ravnima koje

su me|usobno normalne. Po{to su elektri~ne i magnetske oscilacije

normalne na pravac prostiranja svetlosti, mo`e se smatrati da i svet-

lost ima osobine transverzalnog talasa. Na slici 1 prikazan je jedan

svetlosni talas, koji emituje jedan atom, kao elektri~ni oscilator.

U ravni koja je normalna na put prostiranja svetlosti, elektri~ne i

magnetske oscilacije jednog svetlosnog talasa normalne su jedna u

odnosu na drugu (slika 2).

Radi jednostavnijeg izlaganja, u daljem tekstu bi}e prikazan sa-

mo elektri~ni talas u obliku vektora, pri ~emu treba uzeti u obzir da

je magnetski talas uvek spregnut sa elektri~nim, kao i da mu je pra-

vac oscilovanja normalan na pravac oscilovanja elektri~nog talasa.

U tom smislu, pojednostavljena orijentacija svetlosnog talasa prika-

zana je na slici 3.

Eksperimentalna fizi~ka hemija

POLARIMETRIJA

(latinski

polaris

– polarizacija i gr~ki

metria

– merenje)

Teorijski princip

Slika 1.

Svetlosni talas

– talasna du`ina svetlosti

E – amplituda elektri~ne oscilacije

H – amplituda magnetske oscilacije

Slika 2.

Orijentacija svetlosnog talasa

Slika 3.

Orijentacija elektri~nih oscilacija

jednog svetlosnog talasa

Ako se uzme u obzir ogroman broj atoma koji su razli~ito orijen-

tisani u momentu emisije talasa, mo`e se zaklju~iti da se svetlost sas-

toji od velikog broja talasa, ~iji su vektori ravnomerno orijentisani u

svim pravcima, kao na slici 4.

Kad se monohromatska svetlost, a to je veliki broj talasa iste talas-

ne du`ine, propusti kroz jednu vrstu filtera, koji se zove

polaroid

, ta-

da se svi razli~ito orijentisani svetlosni talasi (prikazani na slici 4)

orijenti{u u istom pravcu, tako da se pona{aju kao jedan talas (slika 3).

Takva svetlost naziva se

linearno polarizovana

, {to zna~i da su elek-

tri~ne i magnetske oscilacije usmerene u jednom pravcu, du` celog

puta prostiranja svetlosti. Drugim re~ima, svetlosni vektor (slika 3)

ne menja svoj pravac u slu~aju kad je svetlost linearno polarizovana.

Ravan u kojoj osciluje linearno polarizovan zrak naziva se

ravan

oscilovanja S

, dok se ravan koja stoji normalno na ravan

zove

ravan polarizacije S

, kao na slici 5.

Proces kojim se obi~na svetlost prevodi u polarizovanu naziva se

polarizacija

, a osobinu da se polarizuje ima samo transverzalni ta-

las.

Polaroid se sastoji od vi{e plo~a od stakla ili nekog drugog pro-

zra~nog materijala. Kad svetlosni zrak padne pod uglom na povr{i-

nu prve plo~e, jedan deo zraka se odbije, a drugi, mnogo ve}i deo

svetlosti, pro|e kroz plo~u. Oba zraka se delimi~no polarizuju, a nji-

hove ravni oscilacije su me|usobno normalne. Pri prolazu kroz dru-

gu plo~u polarizacija propu{tenog zraka je jo{ bolja, tako da se pri

izlasku iz polaroida dobija pribli`no linearno polarizovana svetlost.

Mnogi kristali imaju osobinu da polarizuju svetlost. Pri prolasku

kroz islandski kalcit, kvarc, liskun i turmalin, svetlost se razla`e u

dva zraka, od kojih prvi ima iste brzine u svim pravcima kristala i

zove se

redovan

, dok drugi ima razli~ite brzine, u zavisnosti od

pravca kretanja kroz kristal i zove se

neredovan

zrak. Oba zraka su

linearno polarizovana i po izlasku iz kristala se sjedinjuju. Me|utim,

njihove ravni polarizacije su me|usobno upravne, pa je za dobijanje

linearno polarizovane svetlosti potrebno jedan zrak ukloniti. To je

postigao Nikol (Nicol) koji je kristal islandskog kalcita prvo izrezao

tako da dve suprotne ravni stoje pod uglom od 68° prema prirodnim

ravnima kristala. Prizma je, zatim, prerezana po dijagonali, tako da

zahvata ugao od 90° prema spolja{njim ravnima. Prerezane povr{ine

su ugla~ane, pa slepljene prozra~nim kanada-balzamom (slika 6).

Nepolarizovan zrak se, pri prolasku kroz

Nikolovu prizmu

, razla`e

na redovan i neredovan zrak, pri ~emu se redovan zrak totalno re-

flektuje na grani~noj povr{ini izme|u kalcita i kanada-balzama, a

zatim apsorbuje u crnom omota~u prizme. Neredovan zrak prolazi

Medenica / Male{ev

Slika 4.

Ravnomerne orijentacije svetlosnih ta-

lasa u svetlosnom zraku

Slika 5.

Ravan oscilovanja S

i ravan polarizacije S

Neke supstancije pokazuju osobinu da za izvestan ugao okre}u

ravan oscilacije propu{tene polarizovane svetlosti. Ova pojava nazi-

va se

opti~ka rotacija

, a supstancije

opti~ke aktivne

. To su npr. kvarc,

cinober, natrijum-hlorat, terpentin, kristalni {e}er, rastvor {e}era,

strihnin-sulfat i dr. Neke od ovih supstancija okre}u ravan polarizo-

vane svetlosti ulevo, a neke udesno, ako se gleda u pravcu prostiranja

zraka. Za prve se ka`e da su

levogire

, odnosno da imaju

levu

ili

ne-

gativnu rotaciju

, a za druge da su

desnogire

, tj. da imaju

desnu

ili

pozitivnu rotaciju

Postoje supstancije koje su iste po sastavu, a mogu imati suprot-

ne smerove rotacije. Na primer, neki kristali kvarca mogu imati levu,

a neki desnu rotaciju.

Opti~ku aktivnost pokazuju jedinjenja sa asimetri~nom struk-

turom molekula. U mnogim organskim jedinjenjima opti~ka aktiv-

nost poti~e od asimetri~nog ugljenikovog atoma, tj. onog koji je ve-

zan za ~etiri razli~ita atoma ili grupe. Pored ugljenika i atomi drugih

elemenata (N, P, S, Co, Te, Pt) mogu stvoriti jedan ili vi{e asimetri~-

nih ili hiralnih centara u molekulu.

Kada se rastvor opti~ki aktivne supstancije stavi izme|u polari-

zatora i analizatora, ravan oscilacije polarizovanog zraka bi}e pome-

rena za izvestan ugao, zbog ~ega }e intenzitet polarizovane svetlosti

po prolasku kroz analizator biti smanjen. To je shematski prikazano

na slici 9.

Medenica / Male{ev

Slika 8.

Ga{enje polarizovane svetlosti

u analizatoru

Ako se opti~ki aktivna supstancija (npr. {e}er) nalazi u rastvoru,

tada je veli~ina tzv.

ugla rotacije (obrtanja, skretanja)

ravni oscila-

cije polarizovane svetlosti

, koja se izra`ava u radijanima, data jed-

na~inom:

gde je:

– du`ina stuba rastvora u

[

]

c – koncentracija opti~ki aktivne supstancije u

[

gr cm

-3

]

[α]

– konstanta srazmere. Naziva se

specifi~na rotacija

ili

specifi~ni

ugao rotacije (obrtanja, skretanja)

. Zavisi od prirode supstancije,

talasne du`ine monohromatske svetlosti polarizovane pre prolaska

kroz rastvor, kao i temperature rastvora.

Prema jedna~ini (1), specifi~na rotacija defini{e se kao ugao rota-

cije polarizovane svetlosti

, koji izazove rastvor opti~ki aktivne sup-

stancije, ako je du`ina stuba rastvora kroz koji svetlost prolazi 1 dm,

a koncentracija rastvora iznosi 1 gr cm

-3

. Po{to se veli~ina

[α]

iz-

ra`ava u SI jedinicama, prera~unavanje se vr{i tako {to se broj grama

pretvori u kilograme, broj kubnih centimetara u kubne metre, a broj

decimetara u metre, tako da

[α]

ima dimenzije: rad m

-1

Standardni izvori monohromatske svetlosti su `ivina lampa sa

zelenom linijom (

= 546,1 nm) i natrijumova lampa sa `utom D

linijom (

srednje

= 589,3 nm). Ako se za merenje ugla rotacije

ko-

risti natrijumova lampa, a temperatura rastvora iznosi 20°C, onda se

specifi~na rotacija obele`ava

[α]

. Specifi~na rotacija zavisi od ta-

lasne du`ine svetlosti i ova pojava naziva se

rotaciona disperzija

Eksperimentalna fizi~ka hemija

Slika 9.

Skretanje ravni oscilacije polarizovane

svetlosti pri prolasku kroz opti~ki

aktivnu supstanciju

NZ – nepolarizovan zrak

P – polarizator

LPZ

– linearno polarizovan zrak

PC – polarimetarska cev sa opti~ki

aktivnom supstancijom

A – analizator

LPZ

– skretanje ravni linearno

polarizovanog zraka za ugao

[α]

. c

(1)

Monohromatski zrak svetlosnog izvora

(naj~e{}e natrijumova

lampa) prolazi kroz kolimatorsko so~ivo

, koje svetlost u paralel-

nim zracima usmerava ka polarizatoru

. Ako polarizovana svetlost

prolazi kroz polarimetarsku cev

sa vodom, koja nije opti~ki aktiv-

na, polarizator

i analizator

postave se u paralelan polo`aj (slika

7), tako da im se opti~ke ose poklapaju. To se posti`e tako {to se po-

kretna kru`na skala

, koja je povezana sa analizatorom, podesi da

pokazuje nulu (

= 0°). Pri ovim uslovima, polarizovana svetlost

neometano prolazi kroz vodu i analizator i maksimalno osvetljava

vidno polje okulara O.

Pri prolasku polarizovane svetlosti kroz opti~ki aktivan rastvor,

ravan oscilacije polarizovanog zraka skrenu}e za izvestan ugao u od-

nosu na opti~ku osu analizatora, zbog ~ega }e do okulara sti}i polari-

zovana svetlost manjeg intenziteta od maksimalnog. Kada bi ljudsko

oko imalo mo} pam}enja intenziteta svetlosti, analizator bi se po-

mo}u kru`ne skale mogao okrenuti za izvestan ugao

, tako da oku-

lar ponovo bude osvetljen kao kad je u cevi bila voda. To bi zna~ilo

da je ponovo do{lo do poklapanja ravni oscilacije polarizovane svet-

losti sa opti~kom osom analizatora, a ugao koji se pro~ita na kru`noj

skali bio bi jednak uglu rotacije

opti~ki aktivne supstancije.

Me|utim, ljudsko oko je u stanju da uo~ava samo razlike intenzi-

teta svetlosti. Zato je uz polarizator postavljena mala prizma

P’

, koja

pokriva polovinu vidnog polja okulara. Opti~ka osa prizme

P’

zak-

lapa ugao od 2° do 3° sa opti~kom osom polarizatora. Ako se anali-

zator postavi u ukr{ten polo`aj sa polarizatorom (opti~ke ose im se

nalaze pod uglom od 90°), tamnija }e biti ona polovina vidnog polja

koju ne pokriva prizma

P’

. Ako se analizator postavi u ukr{ten polo-

`aj sa prizmom

P’

, bi}e tamnija polovina vidnog polja koju ona po-

kriva. Izme|u ova dva polo`aja postoji srednji, za koji su obe polovine

vidnog polja okulara podjednako osvetljene. Ovaj polo`aj je obele-

`en nulom instrumenta na pokretnoj kru`noj skali

, pod uslovom

da se u polarimetarskoj cevi ne nalazi opti~ki aktivna supstancija,

odnosno kad je u cevi voda. Kad se u cev sipa rastvor opti~ki aktivne

supstancije, jedna polovina vidnog polja bi}e tamnija od druge. Po-

kretni analizator se pomo}u kru`ne skale

dovede u polo`aj da obe

polovine vidnog polja okulara budu podjednako osvetljene, ~ime je

ravan oscilacije polarizovane svetlosti ponovo postavljena pod isti

ugao u odnosu na opti~ku osu analizatora, kao kad je homogena os-

vetljenost vidnog polja pode{ena u odnosu na vodu. Ovaj ugao na

kru`noj skali predstavlja ugao rotacije

, iz koga se pomo}u jedna-

~ine (2) izra~unava procentna koncentracija opti~ki aktivnog rast-

vora.

Eksperimentalna fizi~ka hemija

Polarimetrija se koristi za kvalitativnu i kvantitativnu analizu op-

ti~ki aktivnih jedinjenja, a naro~ito je zna~ajna u obja{njenju stereo-

hemijske strukture opti~kih izomera. U industriji hrane, vo}nih so-

kova i {e}era koristi se za kvantitativnu analizu. Veoma je zna~ajna u

farmaceutskim istra`ivanjima, tako da farmakopeje propisuju ovu

metoda za ispitivanje i kontrolu opti~ki aktivnih jedinjenja, kao {to

su {e}eri, kamfor, etarska ulja i dr. Postoje polarimetri koji su speci-

jalno namenjeni za odre|ivanje koncentracije {e}era. Zovu se

saha-

rimetri

, a skala im je tako kalibrisana da, pri odre|enim uslovima

merenja, na skali neposredno pokazuju sadr`aj {e}era u uzorku koji

se ispituje.

Medenica / Male{ev

Postupak

Uklju~iti natrijumovu lampu preko prekida~a na transformatoru.

Polarimetarsku cev otvoriti sa jedne strane (paziti da se ne polo-

mi staklena plo~ica), isprati sa malo analizirane te~nosti, napuniti je

i zatvoriti tako da ne ostane nimalo vazduha. Cev oprati destilova-

nom vodom i obrisati je, posebno plo~ice koje moraju biti potpuno

~iste. Cev staviti u aparat, a zatim nulu nonijusa poklopiti sa nulom

skale.

Merenja otpo~eti tek kada se dobije intenzivno `uta svetlost lam-

pe. Pomo}u okulara, pomeraju}i ga napred-nazad, podesiti maksi-

malnu o{trinu granice tamnog i svetlog polja. Pomeranjem poluge

pokretne skale udesno, izjedna~iti osvetljenost oba polja i na skali

pomo}u nonijusa pro~itati ugao skretanja ravni polarizovane svet-

losti

. Postupak ponoviti deset puta.

Izra~unavanje

Za pet vrednosti ugla

sa najmanjom apsolutnom gre{kom izra~u-

nati koncentracije, a zatim standardnu devijaciju (poglavlje

Stati-

sti~ka obrada rezultata

u Prilogu):

gde je:

– koncentracija pojedina~nih merenja

< c > – srednja vrednost izra~unatih koncentracija

n – broj merenja.

Izra~unati standardnu devijaciju srednje vrednosti, tj. gre{ku od-

re|ivanja koncentracije:

Podatak za du`inu cevi dat je na samoj cevi (

= 200 mm), a spe-

cifi~na rotacija saharoze iznosi

[α]

= 66,5°.

Rezultate prikazati tabelarno.

Medenica / Male{ev

S = ±

i = 1

– <c>)

n –

<c>

* (°) =

rad/180

= 200 mm

[α]

= 66,5°×10

-2

-1

Eksperimentalna fizi~ka hemija

ERENJE

(°)*

(%)

– < c > (%)

S (%)

< c > ± S (%)

< c >

(%)

–

< >

Tabela 1.

Rezultati merenja

REZULTATI

Kolorimetrija

je vizuelna metoda kojom se na osnovu intenziteta

boje rastvora mo`e odrediti njegova koncentracija. U tu svrhu ko-

riste se instrumenti –

kolorimetri

pomo}u kojih se vr{i pore|enje

intenziteta boje ispitivanog rastvora i rastvora standarda. Po{to se

kao indikator koristi ljudsko oko, ova metoda ne mo`e se smatrati

dovoljno ta~nom. Danas su ovi instrumenti potisnuti iz laboratorija

savremenim fotometrima i spektrofotometrima.

Boja je vizuelni utisak koji se stvara u oku, a javlja se kao posledi-

ca selektivne apsorpcije svetlosti odgovaraju}ih talasnih du`ina

upadne svetlosti (slika 1).

Ako predmet, osvetljen belom svetlo{}u (vidljivi deo spektra),

ostavlja utisak `ute boje zna~i da je propustio `uti deo, odnosno ap-

sorbovao je plavi deo vidljivog spektra. Ako predmet izgleda beo,

zna~i da je upadna svetlost svih talasnih du`ina podjednako pro-

pu{tena ili reflektovana. Naprotiv, ako je predmet crn, zna~i da je ap-

sorbovao upadnu svetlost svih talasnih du`ina.

Ako snop monohromatskog zra~enja (ta~no definisane talasne

du`ine) intenziteta I

pada na neko providno telo, jednim delom

bi}e reflektovan (

), jednim delom apsorbovan (

), a ostali deo

propu{ten (

) (slika 2):

Eksperimentalna fizi~ka hemija

KOLORIMETRIJA

(latinski

color

- boja i gr~ki

metria

- merenje)

Teorijski princip

Slika 1.

Boja kao posledica selektivne

apsorpcije svetlosti

apsorbuje

plavo

apsorbuje

crveno

bela

svetlost

Taraxacum officinale

, masla~ak

Deljenjem ovog izraza sa I

sledi:

Prvi ~lan predstavlja refleksionu, drugi apsorpcionu, a tre}i tran-

sparentnu mo} providnog tela (slika 2). Intenzitet reflektovane svet-

losti

je relativno mali, pa se izraz

mo`e zanemariti.

Smanjenje intenziteta zra~enja, pri prolasku kroz sloj providnog

tela odre|ene debljine (slika 3), definisano je Lamberovim (Lam-

bert) zakonom:

gde je:

k – konstanta srazmere koja zavisi od talasne du`ine upadne svet

losti, prirode supstancije i temperature

I – intenzitet propu{tene svetlosti

dI – deo intenziteta upadne svetlosti koji je apsorbovan

db – debljina sloja kroz koji prolazi svetlost, tzv. du`ina opti~kog puta.

Koeficijent apsorpcije dI/db ima negativan predznak jer je obr-

nuto srazmeran intenzitetu propu{tene svetlosti I.

Preure|enjem i integraljenjem jedna~ine (3) u granicama od I

do I

i b od 0 do b dobija se:

pri ~emu je I

intenzitet upadne, a I

intenzitet propu{tene svetlosti,

odnosno:

Prelaskom na dekadne logaritme dobija se:

Medenica / Male{ev

= I

+ I

(1)

(2)

= 1

Slika 2.

Raspodela upadne svetlosti

pri prolasku svetlosnog zraka

kroz providnu sredinu

–

= k . I

(3)

(4)

Slika 3.

Smanjenje intenziteta zra~enja

I+dI – intenzitet upadne svetlosti

∫

–

∫

= k

(5)

= k . b

– ln

(6)

= k . b

2,303 log

Apsorpcioni koeficijent

ili

apsorptivnost a

je karakteristi~na

veli~ina za svaku molekulsku vrstu i zavisi od prirode rastvorene sup-

stancije, talasne du`ine svetlosti i temperature. Data je jedna~inom:

i defini{e se kao apsorbancija pri prolazu svetlosti kroz sloj jedini~ne

debljine i jedini~ne koncentracije rastvora. Ako se koncentracija iz-

ra`ava u mol L

–1

, naziva se

molarni apsorpcioni koeficijent

Jedna~ina (11) predstavlja matemati~ku formulaciju Lamber-

Berovog zakona. Apsorbancija pokazuje linearnu zavisnost od kon-

centracije odre|ene molekulske vrste, pri prolasku monohromatske

svetlosti (ta~no definisane talasne du`ine), pri stalnoj debljini sloja i

temperature. Smanjenje intenziteta propu{tene svetlosti srazmerno

je broju ~estica u jedinici zapremine rastvora, odnosno koncentraciji

rastvora.

U tabeli 1 date su definicije parametara Lamber-Berovog zakona.

Medenica / Male{ev

b . c

(12)

a =

Tabela 1.

Veli~ine Lamber-Berovog

zakona

Naziv

Simbol

Sinonim

Definicija

Matemati~ka

definicija

Propustljivost

Transparencija

Providnost

Deo upadne svetlosti koji je

propu{ten

Opacitet

–

Recipro~na vrednost transparencije

Apsorpcija

Aps%

–

Deo upadne svetlosti koji je

apsorbovan

Apsorbancija

Ekstinkcija (E)

Opti~ka gustina (OD)

Dekadni logaritam odnosa

upadne i propu{tene svetlosti

Molarna apsorptivnost

Molarni apsorpcioni

koeficijent

Ekstinkcioni koeficijent (

)

Apsorbancija rastvora ~ija je

koncentracija 1 mol L

–1

, a debljina

sloja 1 cm na definisanoj talasnoj

du`ini

Du`ina opti~kog puta

Debljina sloja

Debljina kivete

Du`ina puta kojim prolazi svetlost

kroz odre|enu sredinu

O =

A =

log

b . c

A =

–

Grafi~ki prikaz Lamber-Berovog zakona predstavljen je na slici 4.

Punom linijom prikazana je linearna zavisnost apsorbancije od

koncentracije i predstavlja tzv.

kalibracionu pravu

za odre|enu ta-

lasnu du`inu. Isprekidani delovi krive pokazuju odstupanje od

Lamber-Berovog zakona, koje mo`e nastati usled hemijskih prome-

na npr. disocijacije molekula kod malih koncentracija rastvora ili

pak kod ve}ih koncentracija usled asocijacije, polimerizacije ili stva-

ranja kompleksa. Svako odstupanje od prave linije pokazuje da se is-

pitivana supstancija, u toj oblasti koncentracija, ne pona{a po Lam-

ber-Berovom zakonu.

Kolorimetrijska metoda se zasniva na Lamber-Berovom zakonu.

Koristi se metoda standarda, koja se zasniva na izjedna~avanju in-

tenziteta propu{tene svetlosti kroz uzorak i standard. U tu svrhu

naj~e{}e se koristi

Diboskov

(Dubosq)

kolorimetar

(slika 5).

Eksperimentalna fizi~ka hemija

Slika 4.

Promena apsorbancije

sa koncentracijom rastvora

Slika 5.

Shema Diboskovog kolorimetra

Eksperimentalna fizi~ka hemija

URADITE SAMOSTALNO ...

Odre|ivanje

koncentracije

obojenog rastvora

Zadatak eksperimenta

Pri debljinama sloja standardnog rastvora od b

= 10 i b

= 15

po deset puta izmeriti odgovaraju}e debljine slojeva b

analiziranog rastvora. Iz srednjih vrednosti < b

>, za

odgovaraju}e debljine slojeva b

= 10 i b

= 15, izra~unati

procentne koncentracije analiziranog rastvora c

Iz jedne od dve serije po deset izmerenih vrednosti za b

izdvojiti pet najpribli`nijih i izra~unati standardnu devijaciju S.

Slika 6.

Diboskov kolorimetar

1 – ogledalo

2 – kiveta

3 – cilindri~na prizma

4 – okular

Aparatura i hemikalije

Diboskov kolorimetar (slike 5 i 6)

Obojen rastvor poznate i nepoznate koncentracije

Kalibracija kolorimetra

Prizme i kivete pa`ljivo oprati destilovanom vodom, a zatim rastvo-

rom poznate koncentracije (standardom). U obe kivete sipati stan-

dardni rastvor, a zatim pomo}u levog i desnog zavrtnja spustiti priz-

me tako da debljine slojeva (rastojanje od dna kivete do donje

povr{ine prizme uronjene u rastvor), koje se mogu pro~itati na ska-

lama, budu jednake: b

= 15.

Ogledalo podesiti tako da levo i desno polje u okularu budu

maksimalno osvetljeni. Nagib ogledala ne sme se menjati do kraja

eksperimenta.

Ako polja u okularu nisu podjednako osvetljena, pomerati desnu

prizmu sve dok se polja ne izjedna~e. Kalibracija se vr{i tako {to se

specijalnim zavrtnjem podesi desna skala kako bi debljina sloja po-

novo pokazivala vrednost b

= 15.

Merenje

Desnu kivetu isprati i napuniti rastvorom nepoznate koncentracije,

a zatim prizmu pomerati dok se intenziteti oba polja ne izjedna~e.

Debljinu sloja b

pro~itati na nonijusu, pomeriti prizmu u krajnji

gornji polo`aj, ponovo izjedna~iti intenzitete polja u okularu i pro-

~itati vrednost b

. Ova merenja ponoviti deset puta.

Levu kivetu sa standardnim rastvorom postaviti tako da debljina

sloja kroz koju svetlost prolazi bude b

= 10 i, na ve} opisan na~in,

izvr{iti deset merenja za b

Rezultate prikazati tabelarno.

NAPOMENA:

Prizme postaviti u krajnji gornji polo`aj prilikom

postavljanja i menjanja kiveta, da ne bi do{lo do o{te}ivanja prizmi.

Medenica / Male{ev

Eksperimentalna fizi~ka hemija

Fotometrija

je metoda za odre|ivanje koncentracije obojenih rast-

vora. Zasniva se na neposrednom merenju intenziteta propu{tene

svetlosti I

kroz analizirani rastvor, iz koga se izra~unava koncen-

tracija pomo}u Lamber-Berovog zakona:

gde je:

a – apsorpcioni koeficijent koji predstavlja apsorpcionu mo} sup-

stancije na datoj talasnoj du`ini

b – du`ina svetlosnog puta kroz rastvor

c – koncentracija analiziranog rastvora

– intenzitet upadne svetlosti

– intenzitet propu{tene svetlosti.

Jedan od na~ina odre|ivanja koncentracije analiziranog rastvora

sastoji se u tome da se izmeri intenzitet propu{tene svetlosti I

, pri

~emu je intenzitet upadne svetlosti pode{en na 100%. Pomo}u jed-

na~ine (1) izra~unava se koncentracija

Vrednost apsorpcionog koeficijenta

odre|uje se, tako|e, iz jed-

na~ine (2), merenjem intenziteta svetlosti propu{tene kroz isti rast-

vor poznate koncentracije.

Naj~e{}e primenjivana metoda za odre|ivanje koncentracije

rastvora je

metoda standarda

. Kod ove metode nije potrebno znati

vrednost apsorpcionog koeficijenta. Prema Lamber-Berovom zako-

nu za rastvor poznate koncentracije va`i:

FOTOMETRIJA

(gr~ki

fotos

– svetlost i

metria

– merenje)

Teorijski princip

(1)

a . b . c

A =

log

(2)

c =

log

a . b

(3)

= a . b . c

a za isti rastvor nepoznate koncentracije:

gde je proizvod

isti za oba rastvora.

Deljenjem prethodnih jedna~ina dobija se izraz za izra~unavanje

nepoznate koncentracije:

Kod primene metode standarda treba voditi ra~una da koncen-

tracije standardnog i analiziranog rastvora budu dovoljno bliske,

tako da linearna zavisnost A = f(c) va`i u intervalu ovih koncentra-

cija (str 95).

Instrumenti kojima se meri intenzitet zra~enja, propu{tenog

kroz analizirani rastvor, nazivaju se

fotometri

ili

fotoelektri~ni ko-

lorimetri

. Na slici 1 prikazana je opti~ka shema fotoelektri~nog ko-

lorimetra s jednom foto}elijom. Pored ovih postoje i fotometri sa

dve foto}elije, odnosno sa dva odvojena svetlosna snopa, ~ime se eli-

mini{u gre{ke koje bi mogle nastati usled promene intenziteta svet-

losnog izvora.

Izvor polihromatske svetlosti (volframova sijalica) emituje belu

svetlost koja se, prolaskom kroz kolimatorsko so~ivo, usmerava u

paralelnim snopovima na monohromator. Kod fotometara, mono-

hromatori su selektivni apsorpcioni filtri koji propu{taju spektralne

trake talasnih du`ina u opsegu od 30 do 50 nm. To su obi~no poli-

Medenica / Male{ev

= c

(5)

(4)

= a . b . c

Slika 1.

Opti~ka shema

fotoelektri~nog kolorimetra

W – volframova sijalica

S – kolimatorsko so~ivo

F – filtar

K – odeljak za kivete (A – analizirani

rastvor, S – slepa proba)

D – detektor

P – potenciometar

A – miliampermetar

bancije (A), tako {to se 100% T poklapa sa A = 0. Po{to je T = I

za transparenciju u procentima va`i:

Cela skala u T% mo`e se podesiti tako da bude jednaka intenzite-

tu upadne svetlosti I

. Po{to je skala podeljena na 100 jednakih delo-

va, va`i jednakost I

= 100. Zamenom u jedna~inu (6), dobija se da

je T% = I

. Prema tome, na skali se mo`e istovremeno pro~itati

vrednost T%, odnosno I

i odgovaraju}a apsorbancija, koja se izra-

~unava iz izraza:

Merenja se vr{e tako {to se svetlost prvo propu{ta kroz kivetu sa

rastvara~em, koji se naziva slepa proba. Igla instrumenta zauze}e ne-

ki polo`aj na skali. Pomo}u odgovaraju}eg potenciometra podesi se

igla na 100% T, odnosno na A = 0, ~ime se kompenzuje apsorpcija

koja poti~e od kivete i rastvara~a.

Propu{tanjem svetlosti kroz kivetu sa analiziranim rastvorom,

igla }e se zaustaviti na vrednosti apsorbancije, koja je srazmerna

koncentraciji rastvorka.

Iz izmerenih vrednosti apsorbancija standardnog i analiziranog

rastvora

i poznate koncentracije standardnog rastvora

prema jedna~ini (5) izra~unava se koncentracija rastvora

Fotometrija je na{la {iroku primenu u svim analiti~kim labora-

torijama, naro~ito biohemijskim, koje imaju veliki broj oficinalnih

postupaka kvantitativne apsorpcione fotometrije pri odre|ivanju

mnogih parametara va`nih u biohemiji.

Medenica / Male{ev

T% =

. 100

(6)

100

A =

log

(7)

Aparatura i hemikalije

Fotometar MA 9507 I

SKRA

– Kranj (slika 3)

Obojeni rastvor poznate i nepoznate koncentracije

URADITE SAMOSTALNO ...

Odre|ivanje
koncentracije
obojenog rastvora

Zadatak eksperimenta

Izvr{iti po pet merenja apsorbancija A i intenziteta propu{tene

svetlosti I za rastvore poznate i nepoznate koncentracije.

Iz srednjih vrednosti izra~unati procentnu koncentraciju rastvora,

posebno preko pro~itane i izra~unate vrednosti apsorbancija.

Slika 3.

Fotometar MA 9507 I

SKRA

– Kranj

1 – zavrtanj za korekciju mehani~kog

nultog polo`aja kazaljke

2 – mre`ni prekida~

3 – preklopnik

PRIPRAVA

MERITEV

(priprema-merenje)

4 – indikatorsko svetlo

5 – filtar u opti~kom sistemu

6 – kiveta u opti~kom sistemu

7 – potenciometar grube regulacije A = 0

8 – potenciometar fine regulacije A = 0

9 – filtri u spremi{tu

10 – stalak za kivete

Eksperimentalna fizi~ka hemija

Priprema

Prema boji analiziranog rastvora izabrati odgovaraju}i filtar kom-

plementarne boje (tablica 1, str 87) i postaviti u opti~ki sistem.

Eksperimentalna fizi~ka hemija

ERENJE

TANDARD

(c = ..... %)

(%)

NALIZIRANI RASTVOR

(%)

< n >

Tabela 1.

Rezultati merenja apsorbancije i transparencije

REZULTATI

Tabela 2.

Rezultati izra~unavanja koncentracije

ERENJEM APSORBANCIJE

ERENJEM TRANSPARENCIJE

< A

(%)

< I

< A

(%)

Eksperimentalna fizi~ka hemija

Spektrofotometrija

je metoda koja izu~ava apsorpciju ta~no defini-

sanog monohromatskog zra~enja dobijenog specijalnim prizmama

ili re{etkama. Apsorbovano zra~enje prouzrokuje energetske pro-

mene u molekulu. Od ukupne koli~ine zra~enja supstancija apsor-

buje samo one frekvencije, odnosno onu energiju zra~enja koja mo-

`e izazvati energetske promene stanja u atomu ili molekulu date

supstancije. Na slici 1 prikazana je podela elektromagnetskog zra-

~enja, uz prikaz talasnih du`ina, odnosno frekvencija, a u tabeli 1 i

dejstvo zra~enja na molekul.

Tip zra~enja

Talasna du`ina

Dejstvo zra~enja

zraci

100 fm – 100 pm

jonizacija

zraci

6 pm – 100 nm

jonizacija

100 – 390 nm

pobu|ivanje elektrona

VIS

390 – 800 nm

pobu|ivanje elektrona

800 nm – 200

pobu|ivanje oscilacija

mikrotalasi

200

m – 10 cm

pobu|ivanje rotacija

radiotalasi

> 10 cm

pobu|ivanje rotacija

Apsorpcija zra~enja u ultraljubi~astoj (UV) i vidljivoj (VIS) ob-

lasti izaziva pobu|ivanje (ekscitaciju) elektrona, pa se

UV/VIS ap-

sorpciona spektroskopija

naziva jo{ i

elektronska spektroskopija

Ovom metodom prou~avaju se spektri supstancija u molekulskom

stanju, pa se na osnovu analize spektra mogu protuma~iti i struktu-

re molekula.

Nosioci apsorpcije u molekulu su male atomske grupe, tzv.

hro-

mofore

. Apsorpcija hromofora poti~e od elektronskih prelaza sa os-

novnog na vi{i nivo (n

*, n

*), koji se de{avaju zbog

apsorpcije odre|enih frekvencija zra~enja. U tabeli 2 prikazane su

neke hromofore i odgovaraju}e vrednosti talasnih du`ina pri kojima

se de{avaju elektronski prelazi.

SPEKTROFOTOMETRIJA

Teorijski princip

Slika 1.

Podela elektromagnetskog zra~enja

Tabela 1.

Elektromagnetsko zra~enje

Kvantitativna analiza se zasniva na Lamber-Berovom zakonu. Za

izra~unavanje koncentracije analiziranog rastvora naj~e{}e se koristi

metoda kalibracione krive

Merenje apsorbancije vr{i se na talasnoj du`ini na kojoj anali-

zirani rastvor najvi{e apsorbuje (ili nekoj drugoj optimalnoj talasnoj

du`ini), ~ime se posti`e najve}a osetljivost metode, koja je data ko-

eficijentom

∆

c. Za niz rastvora poznatih koncentracija izmere se

apsorbancije na talasnoj du`ini

max

i konstrui{e dijagram A = f(c)

(slika 3). Iz izmerene apsorbancije

za rastvor nepoznate koncen-

tracije, sa kalibracione krive se grafi~kim putem odredi

, kako je

ozna~eno na slici 3.

Za merenje apsorpcionih spektara koriste se opti~ki instrumenti

–

spektrofotometri

(slika 4).

Eksperimentalna fizi~ka hemija

Slika 3.

Kalibraciona kriva

– apsorbancija rastvora nepoznate

koncentracije

– nepoznata koncentracija

Slika 4.

Shema jednokanalnog spektrofotometra

L – izvor kontinualnog zra~enja

S – kolimatorsko so~ivo

UR – ulazni razrez

M – monohromator

IR – izlazni razrez

K – kiveta sa rastvorom

F – fotodetektor

R – ure|aj za merenje i registrovanje

fotostruje

Osnovni delovi spektrofotometra su:

Izvor svetlosti

Monohromator

Fotodetektor

Kod apsorpcione spektrofotometrije koriste se

izvori

sa kontinu-

alnim zra~enjem. Postoje dva tipa ovih izvora zra~enja:

1. termi~ki

2. izvori sa elektri~nim pra`njenjem.

Termi~ke izvore zra~enja

predstavljaju lampe sa vlaknom, odnos-

no zagrevnom niti ili spiralom od nekog te{ko topivog metala, npr.

volframa ili njegove legure. Ovi izvori koriste se za vidljivu, blisku

ultraljubi~astu i blisku infracrvenu oblast spektra, odnosno u oblasti

talasnih du`ina od 350 do 1000 nm. Kako se volframovo vlakno vre-

menom oksidi{e, to mo`e do}i do promene spektralne raspodele

emitovane svetlosti, o ~emu se mora voditi ra~una tokom spektrofo-

tometrijskih merenja. Kod savremenijih instrumenata danas se sve

vi{e koristi kvarc-jodna lampa u oblasti od 300 do 1000 nm.

Izvore sa elektri~nim pra`njenjem

predstavljaju vodoni~na i deu-

terijumova lampa. To su kvarcne cevi napunjene vodonikom ili deu-

terijumom, u kojima se vr{i elektri~no pra`njenje. Primenjuju se u

opsegu talasnih du`ina od 160 do 380 nm.

Monohromatori

su opti~ki delovi spektrofotometra koji izdvajaju

monohromatsku svetlost, odnosno svetlost odre|ene, ta~no defini-

sane talasne du`ine. Kao monohromatori naj~e{}e se koriste

opti~ke

prizme

difrakcione re{etke

. Svetlosni zrak se prelama na grani~nim

povr{inama prizme i prolaze}i kroz prizmu menja svoj pravac. Izlaz-

ni ugao svetlosnog zraka ima razli~ite vrednosti za razli~ite talasne

du`ine. U vidljivoj oblasti mogu se koristiti prizme od opti~kog

stakla, jer ne apsorbuju vidljivu oblast spektra. U UV oblasti se ko-

riste samo prizme od kvarca, jer prizme od opti~kog stakla apsorbu-

ju UV zra~enje.

Difrakcione re{etke su staklene plo~ice na kojima su urezane lini-

je (otvori) na podjednakom rastojanju jedna od druge. Na mestima

ureza dolazi do difrakcije svetlosnog snopa. Zraci ve}e talasne du-

`ine imaju ve}i ugao skretanja. Nedostatak difrakcionih re{etki je u

tome {to daju spektre vi{eg reda, odnosno monohromatski zrak sa-

dr`i i strane talasne du`ine.

Medenica / Male{ev

oblasti. Ova foto}elija nije pogodna za rad sa malim intenzitetima

svetlosti, jer se dobija mali intenzitet fotostruje, a time i mala oset-

ljivost metode za odre|ivanje koncentracije.

Fotomultiplikator

je ure|aj za merenje malih intenziteta svet-

losti. Koristi se da bi se poja~ao signal, odnosno intenzitet primarne

fotostruje (slika 7).

Fotoni upadne svetlosti koji padaju na katodu izbijaju elektrone,

koji se usmeravaju ka anodi. Zbog postojanja elektri~nog polja, elek-

troni dobijaju veliku kineti~ku energiju, pa iz susedne elektrode (di-

node) izbijaju vi{e novih elektrona. Pomenuti proces ponavlja se u

zavisnosti od broja postavljenih dinoda i ja~ine elektri~nog polja. Na

ovaj na~in primarna fotostruja mo`e se uve}ati i sto hiljada puta.

U spektrofotometru se nalaze dve foto}elije (crvena i plava), a iz-

bor zavisi od dela spektra u kome se vr{e merenja. Karakteristi~na

veli~ina je tzv.

ta~ka prelaza

, koja predstavlja talasnu du`inu na ko-

Medenica / Male{ev

Slika 6.

Vakuumska foto}elija

Slika 7.

Fotomultiplikator

A – anoda

K – katoda

D – dinoda

Eksperimentalna fizi~ka hemija

joj obe foto}elije pokazuju istu osetljivost, odnosno istu apsorbanci-

ju. Ona se obi~no nalazi na oko 625 nm i povremeno se mora kon-

trolisati.

Opti~ki deo spektrofotometra

~ine kolimatorsko so~ivo, razrez,

ogledala i kivete. Opti~ki sistem slu`i da usmeri svetlosne zrake kroz

spektrofotometar, kao i da smanji gubitak (rasejanje) svetlosnog

zraka.

Kolimatorsko so~ivo

slu`i da svetlost, koja se pri prolasku kroz

ulazni razrez prostire na sve strane, usmeri u paralelnom snopu ka

monohromatoru.

Ulazni razrez

ima ulogu da bude predmet, ~iji se

monohromatski lik formira u ravni izlaznog razreza. [irinom

izlaz-

nog razreza

odre|uje se interval talasnih du`ina svetlosti u kome se

nalazi svetlosni talas koji izlazi iz monohromatora.

Staklene kivete

koriste samo u vidljivom delu spektra, jer apsorbuju UV zra~enje, a

kvarcne mogu i u vidljivoj i UV oblasti spektra.

Osim jednokanalnih, postoje i dvokanalni spektrofotometri ~ija

je prednost u istovremenom merenju slepe probe i analiziranog rast-

vora, ~ime se izbegava promena intenziteta upadnog zra~enja, koja

mo`e nastati izme|u pojedina~nog merenja slepe probe i uzorka.

Apsorpcioni spektar (spektrofotogram)

U odre|enom opsegu talasnih du`ina izmeriti apsorbancije jednog

od pripremljenih rastvora (npr. rastvora najve}e koncentracije) i na-

crtati apsorpcioni spektar (slika 2). Talasna du`ina na kojoj rastvor

najvi{e apsorbuje obele`ava se sa

max

. Merenjem apsorbancija na

ovoj talasnoj du`ini posti`e se najve}a osetljivost metode.

Merenja vr{iti na polo`aju

blue

(plava foto}elija) sa pomakom

od 10 nm.

Konstruisanje kalibracione krive

Izmeriti apsorbancije svih {est pripremljenih rastvora poznatih

koncentracija na

max

. Kivetu prethodno isprati rastvorom ~ija se

apsorbancija meri, da ne bi do{lo do promene koncentracije.

Konstruisati dijagram funkcije A = f(c) (slika 3), u kome sve ta~-

ke treba da le`e na pravoj koja je definisana Lamber-Berovim zako-

nom. Ova

kalibraciona kriva

slu`i za odre|ivanje koncentracije

rastvora grafi~kim putem.

Odre|ivanje nepoznate koncentracije

Za rastvor nepoznate koncentracije

izmeriti apsorbanciju na

max

Koncentraciju odrediti grafi~kim putem, kao {to je prikazano na

slici 3.

Rezultate prikazati tabelarno i grafi~ki.

NAPOMENA:

Pri konstruisanju kalibracione krive voditi ra~una da

numeri~ku podelu apsorbancije i koncentracije treba po~eti od

»nule«, kao {to je predstavljeno na slici 3.

Eksperimentalna fizi~ka hemija

101

Medenica / Male{ev

102

REZULTATI

Tabela 1.

Priprema rastvora

Tabela 2.

Apsorpcioni spektar

(%)

(mL)

Tabela 3.

Kalibraciona kriva

c (%)

Tabela 4.

Grafi~ko odre|ivanje nepoznate koncentracije

(%)

(nm)

max

= ...... nm

max

= ...... nm

= .......%

= 25 mL

Medenica / Male{ev

104

Uklju~ivanje aparata

Uklju~iti aparat u struju preko stabilizatora napona.

Okrenuti glavni preklopnik (5) sa leve strane mernog instru-

menta sa polo`aja

(isklju~eno) na

zero

(nula) i pri~ekati 10 mi-

nuta da se lampa zagreje i stabilizuje.

Priprema za merenje

Izvaditi nosa~ kiveta (3) i u polo`aj »1« staviti kivetu sa rastvara~em

– slepa proba (destilovana voda), a u polo`aj »2« kivetu sa rastvorom.

Nosa~ vratiti tako da se bela strelica poklopi sa brojem »1« na pok-

lopcu nosa~a (svetlosni snop tada prolazi kroz rastvara~). Postaviti

radnu talasnu du`inu (6) i izabrati odgovaraju}u talasnu du`inu (4).

Slika 9.

Opti~ka shema spektrofotometra

Unicam

SP 600

1 – izvor svetlosti (volframova lampa)

2 – ogledalo

3 – otvor (slit)

4 – monohromator (staklena prizma)

5 – kivete

6 – zastor foto}elija

7 – plava foto}elija

8 – crvena foto}elija

Eksperimentalna fizi~ka hemija

105

Merenje

a) Pode{avanje elektri~ne nule:

pri polo`aju glavnog preklopnika

zero

, potenciometrom (7) sa oznakom

zero

podesiti iglu mer-

nog instrumenta (10) na sredinu skale (nula skale). Ovim se elimi-

ni{e

tamna struja

koja poti~e od tzv. »lutaju}ih elektrona« u foto}eli-

ji, a koja nije posledica osvetljenosti foto}elije.

b) Pode{avanje nule instrumenta:

pri unapred izabranoj talasnoj

du`ini

vawelength

, glavni preklopnik okrenuti sa

zero

na »100%«

i regulatorom (8) sa oznakom

slit width

({irina otvora) podesiti

{irinu otvora kroz koji prolazi svetlost, tako da se igla mernog in-

strumenta ponovo vrati na nulu. Na ovaj na~in elimini{e se apsor-

bancija slepe probe, odnosno rastvara~a i kivete na talasnoj du`ini

merenja apsorbancije rastvora.

c) O~itavanje apsorbancije:

poklopac nosa~a kiveta pomeriti u po-

lo`aj »2« (svetlost prolazi kroz ispitivani rastvor), a glavni preklopnik

postaviti na

test

(uzorak). Potenciometrom iznad skale sa ozna-

kom

absorbance

(apsorbancija) (9) ponovo podesiti iglu mernog

instrumenta na nulu. Preklopnik

vratiti

zero

i pro~itati vrednost

apsorbancije na donjoj skali. Vrednosti na gornjoj skali predstavljaju

transparentnost, tj. propu{tenu svetlost.

Operacije pod a), b) i c) ponavljati za svaku narednu talasnu du-

`inu, s tim {to se pode{avanje elektri~ne nule ne mora vr{iti ako je

napon napajanja stabilan.

PA@NJA:

1. Proveriti da li je glavni preklopnik vra}en sa polo`aja

test

polo`aj

zero

u toku o~itavanja vrednosti apsorbancija.

Za talasne du`ine

< 400 nm koristiti filtar br. 2, a za

> 400 nm

filtar br. 1.

Za talasne du`ine

< 625 nm koristiti plavu, a za

> 625 nm

crvenu foto}eliju.

Eksperimentalna fizi~ka hemija

109

Elektroliza

je proces razlaganja elektrolita pod uticajem jednosmer-

ne struje. Propu{tanjem jednosmerne struje kroz elektrolit dolazi do

ure|enog kretanja jona (slika 1).

Katjoni

se kre}u ka katodi

na ko-

joj se redukuju:

+ ne

–

Anjoni

se na anodi

oksidi{u predaju}i svoje elektrone anodi:

n–

A + ne

–

Prou~avanjem procesa elektrolize bavio se Faradej (Faraday), ko-

ji je definisao dva osnovna zakona.

Prvi Faradejev zakon.

Masa izdvojene supstancije na elektro-

dama srazmerna je koli~ini propu{tenog elektriciteta:

gde propu{tena koli~ina struje predstavlja proizvod ja~ine struje

(A) i vremena prolaska struje kroz rastvor

(s):

Izdvojena masa ne zavisi od temperature, gustine struje na elektro-

dama, oblika elektroda i suda u kome se izvodi elektroliza.

Drugi Faradejev zakon.

Pri prolasku iste koli~ine struje kroz ra-

zli~ite rastvore elektrolita, na elektrodama se izdvajaju ekvivalentne

mase supstancija, odnosno one stoje u odnosu svojih hemijskih ek-

vivalenata.

Jedinice koli~ine elektriciteta su:

kulon

faradej

(F = 9,65×10

C mol

-1

). Kulon u jedinici vre-

mena prenese ja~inu struje od 1A.

ELEKTROLIZA

Teorijski princip

Slika 1.

Kretanje jona pod dejstvom

jednosmerne struje

(

– katjoni,

– anjoni)

∝

(1)

Q = I . t Q (=) A . s

(2)

Faradej je koli~ina elektriciteta koja na elektrodama izvr{i hemij-

sku izmenu jednog mola nekog jednovalentnog elementa, ili u slu-

~aju vi{evalentnih, jednog ekvivalenta. Ovde je neophodno defini-

sati

hemijski ekvivalent

nekog elementa (iako SI ne prikazuje ovu

veli~inu), odnosno ekvivalentnu masu, koja predstavlja koli~nik

atomske mase i broja elektrona izmenjenih u toku elektrolize. To

zna~i da }e se pri prolasku struje od 1F uvek izdvojiti 108 g Ag, a

bakra dva puta manje od atomske mase bakra, jer je ekvivalentna

masa Cu = atomska masa Cu / 2.

Prema definiciji, ako koli~ina elektriciteta od jednog faradeja iz-

dvoji jedan ekvivalent supstancije, onda }e koli~ina elektriciteta

izdvojiti

kilograma tog elementa:

Iz definicije za ekvivalentnu masu mo`e se napisati:

Zamenom jedna~ine (4) u jedna~inu (3) i re{avanjem po

, do-

bija se matemati~ki izraz drugog Faradejevog zakona:

gde je:

M – molarna masa (kg mol

-1

)

z – broj elektrona izmenjenih elektrolizom.

Koli~nik M/z F naziva se

elektrohemijski ekvivalent e

. Pred-

stavlja konstantu proporcionalnosti izme|u mase i koli~ine elektri-

citeta, a zavisi od prirode supstancije koja reaguje na elektrodama.

To je masa supstancije u kg, koju izdvaja 1C.

Uvo|enjem elektrohemijskog ekvivalenta

u jedna~inu (5) do-

bija se izraz za izra~unavanje mase izdvojene supstancije u toku

elektrolize:

Medenica / Male{ev

110

: 1

eq = Q

(3)

eq =

(4)

m =

(5)

m = e . Q

(6)

Elektrode su uronjene u elektrolit koji se sastoji od vodenog rast-

vora bakar(II)-sulfata kome je dodata mala koli~ina sulfatne kiseline

i izvesna koli~ina etanola. Sulfatna kiselina suzbija hidroliti~ko de-

jstvo vode na bakar(II)-sulfat i pojavu bakar(I)-jona, nastalih ne-

potpunom redukcijom bakar(II)-jona na katodi. Etanol spre~ava

oksidaciju ve} nastalog bakra.

Maksimalna ja~ina struje koja prolazi kroz elektrolit u toku elek-

trolize izra~unava se iz izraza:

gde je:

P – povr{ina uronjenog dela elektrode

j – gustina struje (j = I/P).

Povr{ina elektrode mno`i se sa 2, jer se bakar talo`i na obe strane

elektrode.

Optimalna gustina struje za bakrov kulometar je j = 0,01 – 0,02 A

-2

, jer se pri tim uslovima dobija najkompaktniji sloj istalo`enog

bakra.

Postoje razli~ite vrste kulometara (bakrov, srebrov, jodni, gasni),

prema elementima koji se u kulometrima elektrolizom izdvajaju –

talo`e ili osloba|aju.

Elektri~na shema za izvo|enje elektrolize prikazana je na slici 3.

Propu{tanjem jednosmerne struje kroz bakrov kulometar, na

elektrodama se de{avaju slede}e elektrohemijske reakcije:

Anoda:

+ 2e

–

Katoda:

+ 2e

–

Zna~i da se anoda rastvara, a na katodi dolazi do talo`enja ele-

mentarnog bakra. Prema tome, na osnovu mase istalo`enog bakra

pri ta~no definisanim uslovima elektrolize (

) mo`e se proveriti

Faradejev zakon elektrolize.

Medenica / Male{ev

112

Slika 3.

Elektri~na shema

za izvo|enje elektrolize

S – izvor jednosmerne struje

R – promenljivi otpor

K – kulometar

P – prekida~

A – ampermetar

I =

P . j

(8)

Aparatura

Bakrov kulometar (slika 2)

Akumulator

Ampermetar

Promenljivi otpornik

Prekida~

Hronometar

Etanol

Priprema

Izmeriti povr{inu uronjenog dela bakarne plo~e (katode).

Izra~unati ja~inu struje (

) i vreme (

), koji su potrebni da se ista-

lo`i zadata masa bakra (

), kada je gustina struje j = 0,01 A cm

-2

(e = 0,3294 mg C

-1

Bakarnu katodu o~istiti {mirgl-papirom ili razbla`enom nitrat-

nom kiselinom, oprati destilovanom vodom, zatim etanolom i osu-

{iti. Izmeriti masu katode na analiti~koj vagi sa ta~no{}u ~etiri deci-

malna mesta (masa m

Postupak

Prema shemi za elektrolizu (slika 3), spojiti sve elemente aparature.

U momentu uklju~ivanja kola struje uklju~iti hronometar i ot-

pornikom podesiti ja~inu struje na izra~unatu vrednost

. U toku

elektrolize odr`avati konstantnu ja~inu struje pomo}u otpornika.

Nakon izvr{ene elektrolize (po isteku vremena

) izvaditi katodu iz

kulometra, preliti je destilovanom vodom, zatim etanolom, osu{iti i

izmeriti (masa m

). Na}i razliku m

– m

Radne uslove i rezultate merenja prikazati tabelarno.

Eksperimentalna fizi~ka hemija

113

URADITE SAMOSTALNO ...

Provera

Faradejevog zakona

Zadatak eksperimenta

Istalo`iti zadatu masu bakra i proveriti Faradejev zakon

elektrolize.

Eksperimentalna fizi~ka hemija

115

Kulometrijske metode

se zasnivaju na merenju koli~ine elektricite-

ta koja je protekla u toku elektrolize. Osnovni zahtev za sva kulo-

metrijska odre|ivanja je kvantitativna reakcija na elektrodama, uz

100%-tno iskori{}enje struje. To zna~i da se elektrodna reakcija odi-

grava kvantitativno u saglasnosti sa Faradejevim zakonima elek-

trolize, bez paralelnih sekundarnih reakcija. Struja elektrolize ne

sme se tro{iti na nekontrolisane, tj. konkurentne reakcije koje bi

ometale 100%-tno iskori{}enje struje.

Kulometrijska merenja mogu se izvoditi ili pri konstantnom po-

tencijalu ili pri konstantnoj ja~ini struje.

Kulometrija pri konstantnom potencijalu

zasniva se na elektrolizi

rastvora pri konstantnoj, unapred odabranoj, vrednosti potencijala

radne elektrode. Izbor potencijala radne elektrode vr{i se na os-

novu krive ja~ina struje – vreme za ispitivanu supstanciju (slika 1).

Pri konstantnoj vrednosti potencijala struja eksponencijalno

opada sa smanjenjem koncentracije supstancije:

gde je:

– ja~ina struje u vremenu t

– po~etna ja~ina struje

k – konstanta koja zavisi od prirode analizirane supstancije i eksperi-

mentalnih uslova.

Koli~ina elektriciteta proporcionalna je povr{ini ispod krive:

Kulometrija pri konstantnoj ja~ini struje

izvodi se uz odr`avanje

konstantne ja~ine struje. Koli~ina elektriciteta jednaka je proizvodu

ja~ine struje i vremena (slika 2):

Ova metoda koristi se kod kulometrijskih titracija.

KULOMETRIJSKA TITRACIJA

Teorijski princip

Slika 1.

Kriva ja~ina struje–vreme

pri E = const.

= I

. e

–k . t

(1)

Q = I . t

(3)

(2)

∫

. dt

Kulometrijska titracija

doslovce zna~i »titracija kulonima«, tj.

»titracija strujom«. To zna~i da se iz izmerene koli~ine elektriciteta,

odnosno protekle konstantne ja~ine struje u toku vremena

trajanja

elektrolize, mo`e odrediti koncentracija analiziranog rastvora.

Prema na~inu izvo|enja, kulometrijske titracije mogu biti

nepo-

sredne

posredne

Kod neposredne kulometrijske titracije ispitivani elektrolit ne-

posredno reaguje na odgovaraju}oj elektrodi na ta~no definisani na-

~in. Kod ovih titracija, koje se izvode pri konstantnom potencijalu,

te{ko je na}i na~in odre|ivanja zavr{ne ta~ke titracije (Z.T.T.), pa se

retko koristi.

Posredna

kulometrijska titracija izvodi se tako {to se na jednoj

od elektroda, na ta~no poznat na~in, odvija elektrohemijski proces

uz 100%-tno iskori{}enje struje. Na toj elektrodi se elektroliti~kim

putem stvara titrant koji zatim kvantitativno reaguje sa analizira-

nom supstancijom, {to se mo`e prikazati na slede}i na~in:

A + ne

–

B + C

proizvod reakcije

gde je:

A – titrant prekursor (primarni titrant)

B – elektrogenerisani titrant

C – analizirani rastvor.

Medenica / Male{ev

116

Slika 2.

Grafi~ki prikaz funkcije Q = f(t)

kod kulometrije pri konstantnoj

ja~ini struje

hlorida ili kalijum-nitrata. Na taj na~in se spre~avaju reakcije izme-

|u proizvoda nastalih elektrohemijskim procesima na elektrodama.

Gre{ke u toku kulometrijskih merenja mogu nastati usled varija-

cija u struji ili ako se ne mogu precizno meriti ja~ina struje ili vreme.

Kulometrijska titracija mo`e se koristiti pri svim procesima neu-

tralizacije, talo`enja, oksidoredukcije i stvaranja kompleksa. Zbog

toga je ova elektrohemijska metoda na{la {iroku primenu u mnogim

farmaceutskim istra`ivanjima, naro~ito u ispitivanju i kontroli leko-

va, kao i u toksikolo{koj hemiji i biohemiji.

Prednost kulometrijske titracije le`i u jednostavnosti aparature,

kao i u velikoj preciznosti metode. Posebno je zna~ajno to {to se ti-

trant elektrogeneri{e, a to je veoma zna~ajno kod titranata koje je te-

{ko pripremiti, hemijski standardizovati i ~uvati zbog njihove nesta-

bilnosti. To zna~i da se na ovaj na~in mogu koristiti za titraciju i

veoma nestabilni titranti, npr. jod ili brom.

Karakteristi~an primer posredne titracije je odre|ivanje koncentra-

cije natrijum-tiosulfata sa jodom. Kako je jod veoma nestabilan i ne

mo`e se ta~no izvr{iti njegova standardizacija, to je kulometrijska

titracija idealna metoda za ovakve titracije. U anodni prostor sipa se

odre|ena zapremina natrijum-tiosulfata, kalijum-jodida i skroba. U

katodni prostor, koji je odvojen elektroliti~kim mostom od agar-aga-

ra, sipa se kalijum-hlorid kao elektrolit. U toku elektrolize se na ano-

di elektrogeneri{e elementarni jod oksidacijom iz kalijum-jodida:

–

+ 2e

–

koji zatim reaguje sa natrijum-tiosulfatom:

2Na

+ J

+ 2NaJ

Zavr{nu ta~ku titracije predstavlja pojava stabilne plave boje ra-

stvora nastale reakcijom skroba i joda koji se pojavio u vi{ku, jer je

sav natrijum-tiosulfat pre{ao u natrijum-tetrationat.

Medenica / Male{ev

118

Aparatura i hemikalije

Ure|aj za kulometrijsku titraciju (slika 3)

Mehani~ka me{alica

Hronometar

Natrijum-tiosulfat

Kalijum-jodid

Skrob

Priprema

Povezati aparaturu po shemi za izvo|enje kulometrijske titracije. U

anodni prostor (ve}a posuda) odmeriti 50 mL kalijum-jodida, 2 mL

skroba i zadatu zapreminu analiziranog rastvora natrijum-tiosulfa-

ta. U katodni prostor (manja posuda) sipati kalijum-hlorid. Donji

deo manje posude sa poroznim (sinterovanim) dnom prevu~enim

agar-agarom uroniti u rastvor ve}e posude, a zatim u obe staviti od-

govaraju}e elektrode. Anodu predstavlja platinska plo~ica, a katoda

mo`e biti i od bakra. Anodu treba uroniti tako da dr`a~ elektrode

bude van rastvora. Postaviti me{alicu u rastvor i pomo}u otpornika

podesiti brzinu okretanja me{alice tako da se ostvari mirno me{anje

rastvora.

Postupak

Istovremeno uklju~iti kolo struje preko prekida~a i hronometar, a

zatim ja~inu struje odr`avati konstantnom pomo}u promenljivog

otpora. Hronometar isklju~iti u trenutku kad se ceo rastvor oboji

Eksperimentalna fizi~ka hemija

119

DIIT

E S

O ......

Odre|ivanje

koncentracije

natrijum-tiosulfata

Zadatak eksperimenta

Zadatu zapreminu natrijum-tiosulfata titrovati sa

elektrogenerisanim jodom pri odabranoj ja~ini struje. Titraciju

ponoviti tri puta. Iz vremena potrebnog za titraciju i ja~inu struje

izra~unati broj grama natrijum-tiosulfata za svaku titraciju

posebno. Iz srednje vrednosti broja grama < m > izra~unati mo-

larnu koncentraciju natrijum-tiosulfata.

Eksperimentalna fizi~ka hemija

V = ..........mL Na

= 0,001638 g C

-1

121

REZULTATI

Tabela 1.

Eksperimentalni uslovi i rezultati titracije

ITRACIJA

I (A)

t (s)

m (g)

< m > (g)

c (mol L

–1

)

(7)

Potenciometrija

POTENCIOMETRIJSKA MERENJA

Odre|ivanje elektromotorne sile

Potenciometarsko odre|ivanje pH

Merenje pH rastvora pH-metrom

Jon-selektivne elektrode

POTENCIOMETRIJSKA TITRACIJA

Reakcija neutralizacije

Reakcija talo`enja

Potenciometrijska titracija po Pogendorfovoj metodi kompenzacije

Reakcija oksidoredukcije

Ako se cinkana i bakarna elektroda pove`u miliampermetrom,

igla instrumenta }e skrenuti, {to zna~i da je u }eliji do{lo do pojave

elektri~ne struje kao posledice oksidoredukcije. Ako se iz sistema ne

odvodi struja, javi}e se tzv.

ravnote`ni napon

, tj.

elektromotorna

sila

, koja predstavlja razliku potencijala elektroda:

Konvencijom Internacionalne unije za ~istu i primenjenu hemiju

(IUPAC), EMS galvanske }elije prikazuje se kao razlika potencijala

pozitivnije, desne elektrode (na kojoj se vr{i redukcija) i potencijala

negativnije, leve elektrode (na kojoj se vr{i oksidacija).

Potencijal elektrode

nastaje kao posledica stvaranja razlike nae-

lektrisanja izme|u metala i rastvora, odnosno na granici faza me-

tal/rastvor. Naziva se

ravnote`ni potencijal elektrode

, a zavisi od

prirode metala i koncentracije jona metala u rastvoru. Nastanak po-

tencijala elektrode je posledica stvaranja tzv.

dvostrukog elektri~-

nog sloja

na granici faza. Naime, kristalna re{etka metala sastoji se

od odgovaraju}ih jona i elektrona koji se haoti~no kre}u oko jona ~i-

ne}i tzv. »elektronski gas«. Kada se npr. bakarna {ipka uroni u rastvor

bakar(II)-sulfata, postoji te`nja da Cu

joni sa bakarne {ipke pre|u

u rastvor. Posledica ovoga je da na metalu ostaju neneutralisani elek-

troni, pa elektroda postaje u izvesnoj meri negativna, a rastvor pozi-

tivan. Na dodiru faza metal/rastvor, uspostavlja se razlika potencijala

izme|u negativno naelektrisanog metala i pozitivno naelektrisanog

rastvora, kao posledica stvorenog dvostrukog elektri~nog sloja.

Osnovna jedna~ina teorije stvaranja elektrodnog potencijala je

Nernstova

(Nernst)

jedna~ina

za ravnote`ni potencijal elektrode:

gde je:

E0– standardni potencijal elektrode

R – gasna konstanta

T – temperatura

F – koli~ina struje od jednog faradeja (96.485 C mol

–1

)

n – broj elektrona po jonu koji se razmeni u redoks reakciji

– aktivnost oksidovanog oblika metala

red

– aktivnost redukovanog oblika metala

Medenica / Male{ev

126

EMS

–

(1)

EMS

(+)

–

(–)

(2)

red

(3)

Prvi sabirak predstavlja

standardni potencijal E

, odnosno rav-

note`ni potencijal pri odnosu a

red

= 1 i zavisi od prirode sistema.

Standardni potencijali svih elektroda definisani su u odnosu na

standardni potencijal vodoni~ne elektrode, za koju je konvencijom

uzeto da ima potencijal jednak nuli (E

= 0,0000 V) na svim tempera-

turama, pri jedini~noj aktivnosti vodonikovih jona i parcijalnom

pritisku gasa vodonika od 1atm. Na taj na~in formirana je tablica

standardnih potencijala elektroda u kojoj se vodoni~na elektroda

nalazi oko sredine (tablica 7 u Prilogu).

Po{to je 2,303 RT/F = 0,0591 V, za T = 298,15 K (25°C), iz jed-

na~ine (3) sledi:

Jedna~ina (4) predstavlja Nernstov izraz za potencijal elektrode

bilo kog sistema. Za elektrodu I vrste, koju ~ini metal u rastvoru svo-

jih jona, jedna~ina (4) ima oblik:

jer je me|unarodnom konvencijom aktivnost metala definisana kao

jedinica, tj. a

red

= 1.

U izrazu za potencijal koristi se aktivnost jona

, data izrazom:

gde je

– faktor aktivnosti, koji se izra~unava iz jonske ja~ine rastvo-

ra. Samo u slu~aju jako razbla`enih rastvora mo`e se aktivnost izjed-

na~iti sa koncentracijom.

Aktivnost analiziranih jona u rastvoru izra~unava se iz vrednosti

potencijala elektrode. U tu svrhu se indikatorska (merna) elektroda,

~iji potencijal zavisi od aktivnosti analiziranih jona, spre`e sa refer-

entnom (standardnom) elektrodom, ~iji je potencijal poznat i kon-

stantan i ne zavisi od aktivnosti analiziranih jona (slika 2). Potencijal

indikatorske elektrode (E

ind

) izra~unava se iz izraza za elektromo-

tornu silu sprega:

Eksperimentalna fizi~ka hemija

127

EMS

ind

–

ref

(7)

0 +

log

0,0591

red

(4)

0 +

log

0,0591

(5)

(6)

Slika 2.

Galvanska }elija za odre|ivanje poten-

cijala elektrode

Na `ivinoj elektrodi dolazi do reverzibilne reakcije:

+ 2e

–

2Hg

Prema konvenciji, koncentracija redukovanog oblika metala, od-

nosno koncentracija elementarne `ive i drugih ~vrstih supstancija,

jednaka je jedinici, pa prema op{tem Nernstovom izrazu (4) sledi

izraz za potencijal kalomelove elektrode:

Po{to je proizvod rastvorljivosti kalomela:

to se zamenom u jedna~inu (9) dobija:

odnosno:

gde zbir prva dva ~lana predstavlja standardni potencijal kalomelove

elektrode (E

kal

Kona~an izraz za potencijal kalomelove elektrode glasi:

odnosno:

U zavisnosti od koncentracije upotrebljenog kalijum-hlorida,

definisan je i potencijal kalomelove elektrode koji je konstantan i

reverzibilan, pa se ova elektroda koristi kao referentna. Naj~e{}e se

koriste zasi}ena (E = 0,2444 V), molarna (E = 0,2848 V) i 0,1 molar-

na (E = 0,3356 V, na 20°C) kalomelova elektroda.

Eksperimentalna fizi~ka hemija

129

/Hg

(9)

/Hg

–

(11)

/Hg

–

(12)

kal

–

kal

– 0,0591 log

–

(13)

(14)

= a

–

(10)

Medenica / Male{ev

130

Potencijali svih elektroda definisani su u odnosu na

standardnu

vodoni~nu elektrodu

Vodoni~na elektroda

se sastoji od platinske plo~ice uronjene u

rastvor koji sadr`i vodonikove jone i oko kojih se kroz rastvor uvodi

~ist gas vodonik pod odre|enim pritiskom.

Op{ta formula ove elektrode jeste:



(g)



(aq)

Mehanizam uspostavljanja potencijala na platinskom provod-

niku sastoji se u uspostavljanju ravnote`e izme|u jona vodonika u

rastvoru i atomskog vodonika adsorbovanog na platini koja se po-

na{a kao »metalni« vodonik. Zato ova elektroda spada u elektrode

prve vrste. Na njoj se de{ava slede}a polureakcija:

+ 2e

–

Potencijal elektrode dat je Nernstovim izrazom:

odnosno:

Kada je aktivnost vodoni~nih jona

jednaka jedinici (1 mol L

-1

), a pritisak gasa vodonika jednak 1 atm, drugi sabirak u jed-

na~ini (16) jednak je nuli. Pod ovim uslovima vodoni~na elektroda

je uzeta kao

standardna

Prema me|unarodnoj konvenciji, standardni potencijal vodo-

ni~ne elektrode iznosi: E

= 0,0000 V. U odnosu na standardni po-

tencijal vodoni~ne elektrode dati su standardni potencijali drugih

elemenata i elektrodnih reakcija i prikazani u »naponskom nizu ele-

menata«.

Standardna vodoni~na elektroda prikazana je slede}om she-

mom:



(1atm)



= 1,00)

Slika 4.

Vodoni~na elektroda

(15)

(16)

(17)

Kada se izvr{i kompenzacija elektromotorne sile galvanskog

sprega EMS

, mo`e se napisati da je odnos sila EMS

i EMS

jednak

odnosu njihovih otpora, koji su srazmerni du`inama `ica

Umesto galvanskog sprega u sporedno kolo se uklju~i standardni

Vistonov

(Weaston)

element

koji ima poznatu i konstantnu elek-

tromotornu silu EMS

. Kada se kompenzacijom odredi odse~ak l

va`i}e slede}i odnos:

Deljenjem jedna~ine (2) sa jedna~inom (1) dobija se izraz:

iz koga se izra~unava elektromotorna sila galvanskog sprega

EMS

iz poznate vrednosti elektromotorne sile Vistonovog elementa.

Vistonov galvanski element (slika 2) koristi se kao standardni, jer

ima u toku du`eg vremena konstantnu EMS (EMS = 1,0183 V na

20°C) i mali temperaturni koeficijent elektromotorne sile. Koristi se

kao etalon za odre|ivanje EMS drugih galvanskih spregova.

Medenica / Male{ev

132

EMS

(1)

EMS

(2)

EMS

(3)

Slika 2.

Vistonov standardni element

Op{ta shema ovog sprega je:

Cd (Hg)



CdSO

(zasi}en)



, Hg

Pozitivnu elektrodu ~ini `iva iznad koje se nalazi pasta `ive i `iva(I)-

sulfata u zasi}enom rastvoru kadmijum-sulfata. Na njoj se de{ava

redukcija, odnosno slede}a polureakcija:

+ 2e

–

2Hg

Negativnu elektrodu ~ini kadmijum-amalgam u zasi}enom rastvoru

kadmijum-sulfata. Na njoj se de{ava oksidacija, odnosno slede}a

polureakcija:

+ 2e

–

Nastajanje elektromotorne sile u Vistonovom galvanskom

spregu posledica je slede}e elektrohemijske reakcije:

Cd + Hg

+ SO

2–

+ 2Hg + SO

2–

sa elektromotornom silom koja je data jedna~inom:

gde je:

/ 2Hg

– potencijal pozitivne `ivine elektrode

/ Cd

– potencijal negativne kadmijumove elektrode.

Eksperimentalna fizi~ka hemija

133

= E

/2Hg

–

/Cd

(4)

Eksperimentalna fizi~ka hemija

135

REZULTATI

Tabela 1.

Odre|ivanje EMS

(mm)

EMS

(V)

EMS

(V)

Eksperimentalna fizi~ka hemija

137

pH vrednost se defini{e kao negativan logaritam aktivnosti vodoni~-

nih jona u rastvoru:

Potenciometrijsko odre|ivanje pH zasniva se na merenju elek-

tromotorne sile galvanskog sprega metodom kompenzacije (slika 1,

strana 131). Galvanski spreg ~ine merna elektroda (reverzibilna na

aktivnost H

jona) i referentna elektroda koja ima poznat i konstan-

tan potencijal, nezavisan od aktivnosti H

jona. Kao merna elektro-

da naj~e{}e se koristi vodoni~na, hinhidronska ili staklena elektroda.

Galvanski spreg, koji ~ine hinhidronska i kalomelova elektroda,

predstavlja se slede}om usvojenom shemom:

Hinhidronska elektroda

je primer oksidoredukcione elektrode.

Sastoji se od platine uronjene u zasi}en rastvor hinhidrona, koji

predstavlja ekvimolarnu sme{u hinona i hidrohinona. U rastvoru se

de{ava reverzibilna reakcija izme|u hinona (Q) i njegovog reduko-

vanog oblika hidrohinona (H

Q):

Kako potencijal elektrode zavisi od aktivnosti jona u rastvoru (u

ovom slu~aju vodoni~nih jona), izraz za potencijal hinhidronske

elektrode glasi:

POTENCIOMETRIJSKO ODREIVANJE pH

Teorijski princip

pH = –

log

(1)

kalomelova

elektroda

elektroliti~ki

most

hinhidronska elektroda

sa ispitivanim rastvorom

hidrohinon

hinon

Q +

––

Iz izlo`enog sledi, da se merenjem elektromotorne sile galvan-

skog sprega hinhidronske i kalomelove elektrode mo`e izra~unati

pH analiziranog rastvora.

Hinhidronska elektroda je pogodna za upotrebu samo u jako

kiselim i neutralnim rastvorima, tj. do pH 8,0. To je zbog toga {to je

hidrohinon slaba kiselina, pa u alkalnim rastvorima primetno raste

protoliza, odnosno dolazi do promene odnosa koncentracija hinona

i hidrohinona. To uslovljava odstupanje od linearne zavisnosti:

hin

= f(pH)

Pogendorfova metoda kompenzacije koristi se za merenje elek-

tromotorne sile galvanskog sprega ~iji otpor nije veliki. Zato se ovaj

na~in potenciometrijskog odre|ivanja pH mo`e koristiti samo kod

spregova sa vodoni~nom ili hinhidronskom elektrodom.

Eksperimentalna fizi~ka hemija

139

Aparatura i hemikalije

Ure|aj za izvo|enje Pogendorfove metode kompenzacije (slika

1, strana 131)

Galvanski spreg nepoznate EMS

Vistonov standardni element

Platinska elektroda

Kalomelova elektroda

Hinhidron

Elektroliti~ki most od agar-agara

Priprema

U ~a{u sipati rastvor ~ija se pH vrednost odre|uje i dodati toliko

hinhidrona da rastvor bude zasi}en. Potrebna je mala koli~ina hin-

hidrona da bi se dobio zasi}en rastvor, {to se zapa`a plivanjem kri-

stali}a hinhidrona po povr{ini rastvora. Rastvor dobro prome{ati

staklenim {tapi}em i uroniti platinsku elektrodu, vode}i ra~una da

klema koja dr`i platinu ne do|e u kontakt sa rastvorom. Elektroli-

ti~kim mostom od agar-agara povezati hinhidronsku i kalomelovu

elektrodu. Tako je stvoren galvanski spreg ~iju vrednost elektromo-

torne sile treba odrediti.

Postupak

Izmeriti odse~ak kompenzacije

za Vistonov standardni element i

za pripremljeni galvanski spreg. Odrediti elektromotornu silu

EMS

na na~in opisan na strani 134 i izra~unati pH rastvora.

Rezultate prikazati tabelarno.

Medenica / Male{ev

140

URADITE SAMOSTALNO ...

Potenciometrijsko
odre|ivanje pH

Zadatak eksperimenta

Metodom kompenzacije odrediti elektromotornu silu

pripremljenog galvanskog sprega i izra~unati pH rastvora.

Eksperimentalna fizi~ka hemija

143

pH-metar je instrument za neposredno merenje pH rastvora. Gal-

vanski spreg, ~ija se elektromotorna sila meri (a pH vrednosti o~i-

tavaju na skali instrumenta), sastoji se od staklene i kalomelove elek-

trode uronjene u analizirani rastvor.

Staklena elektroda

, zbog velikog otpora, ne mo`e se koristiti kod

Pogendorfove metode kompenzacije. Me|utim, pH-metar je mili-

voltmetar sa veoma velikom unutra{njom otporno{}u tako da pri

merenju uzima iz sprega zanemarljivo male koli~ine struje. Staklena

elektroda je staklena cev na ~ijem se jednom kraju nalazi staklena

polulopta koja se pona{a kao jon-selektivna membrana za hidroni-

jum jone, {to zna~i da je omogu}eno prodiranje hidronijum jona u

kristalnu strukturu membrane (slika 1). U unutra{njosti se nalazi

tzv. unutra{nja referentna elektroda. To je elektroda druge vrste, sre-

bro/srebro-hloridna koja je uronjena u rastvor hloridne kiseline od-

re|ene aktivnosti hidronijum jona (0,1 mol L

–1

). Staklena elektroda

predstavlja se slede}om shemom:

Ag, AgCl



0,1 mol L

–1

HCl



staklena membrana



rastvor

Staklenu membranu ~ini posebno staklo u ~iji sastav pored Si

ulaze i joni Na

, Ca

, K

, »retkih zemalja« i dr. Na dodirnoj

povr{ini faza staklo/rastvor joni natrijuma zamenjuju se hidronijum

jonima. Tako nastaje membranski potencijal, {to ima za posledicu

promenu potencijala unutra{nje referentne elektrode, pri promeni

koncentracije hidronijum jona u rastvoru.

Potencijal staklene elektrode ~ini zbir potencijala unutra{nje refe-

rentne elektrode (E

), potencijala unutra{nje povr{ine staklene

membrane (E

) i potencijala spoljne povr{ine staklene membra-

ne (E

). Ovom zbiru treba dodati i potencijal asimetrije (E

asim

), tj.

potencijal koji se javlja kao posledica neidenti~nosti spoljne i unu-

tra{nje povr{ine staklene membrane. Prema tome je:

Kako su za datu elektrodu prve tri vrste potencijala konstantne, a

zavisi od koncentracije hidronijum jona u rastvoru, izraz za po-

tencijal elektrode je:

MERENJE pH RASTVORA pH-METROM

Teorijski princip

Slika 1.

Staklena elektroda

E = E

+ E

asim

+ E

(1)

odnosno:

gde je E

= E

+ E

asim

= konst., za datu pojedina~nu elek-

trodu.

Asimetri~ni potencijal

nije konstantna vrednost za sve pojedi-

na~ne elektrode i nije isti za sve vrste staklenih elektroda. Predstavlja

merilo asimetrije staklene membrane u pogledu razli~itih osobina

dveju povr{ina membrane nastale u toku proizvodnje, usled nesa-

vr{enosti silikatne strukture. Mehani~ka i hemijska o{te}enja, kao i

kontaminacija u toku du`e upotrebe, tako|e uti~u na vrednost asi-

metri~nog potencijala. Efekat asimetri~nog potencijala na merenja

pH otklanja se povremenom kalibracijom elektrode sa jednim ili

vi{e standardnih pufera poznatih pH vrednosti.

Membranski potencijal na staklenoj elektrodi uspostavlja se pro-

cesom »potiskivanja«, pa je zato elektrodu pre upotrebe potrebno

aktivirati dr`anjem u rastvoru hloridne kiseline. Tada se i na spolja{-

njoj dodirnoj povr{ini faza staklo/rastvor izvr{i odgovaraju}a izme-

na jona natrijuma iz stakla sa hidronijum jonima iz rastvora. Posle

upotrebe elektroda se dr`i u destilovanoj vodi ili ve} kako proizvo-

|a~ savetuje u uputstvu.

Staklena elektroda mo`e pokazivati odstupanje membranskog po-

tencijala od pH vrednosti pri jako niskim vrednostima pH, a tako|e

i pri vrednostima pH>9, {to predstavlja tzv. »kiselu«, odnosno »al-

kalnu« gre{ku. Uzroci nastajanja nisu u potpunosti razja{njeni. Al-

kalna gre{ka mo`e se izbe}i primenom staklene elektrode koja ume-

sto Na

ili Ca

jona sadr`i Li

ili Ba

jon. Ova supstitucija pove}ava

opseg merenja elektrode. Do gre{aka u toku rada mo`e do}i i usled

»dehidratacije« elektrode koja nastaje posle dugotrajnog rada u

nevodenim sredinama ili ako se elektroda dr`i na suvom. U tom slu-

~aju potrebno je elektrodu ponovo aktivirati, a pri radu u nevode-

nim sredinama preporu~uje se povremeno dr`anje elektrode u vodi.

Gre{ke mogu nastati i pri merenju pH koloidnih rastvora, zatim

emulzija i suspenzija zbog indukovanog potencijala ovih naelek-

trisanih ~estica.

Nedostaci staklenih elektroda ogledaju se u visokoj otpornosti,

starenju membrane i pojavi potencijala asimetrije.

Medenica / Male{ev

144

E = E

(2)

E = E

–

0,0591

(3)

pH-metri

su ure|aji koji se zasnivaju na radu cevnog milivolt-

metra koji su danas u potpunosti zamenjeni tranzistorskim mili-

voltmetrima. Iako opis cevnog milivoltmetra (slika 4) gubi na aktu-

elnosti, potrebno je objasniti princip rada, jer se primenjuje i na

na~in rada savremenih digitalnih instrumenata.

Cevni potenciometar se sastoji od triode, kod koje katoda

ima

sopstveno napajanje

. Kada se katoda zagreje, emituje elektrone

koji se kre}u ka anodi

. Ja~ina anodne struje, koja se meri na am-

permetru

, zavisi od napona koji je saop{ten katodi i anodi sa izvo-

ra jednosmerne struje

. Izme|u katode i anode postavljena je

mre`ica

kroz koju elektroni mogu nesmetano prolaziti ukoliko

nije vezana za neki galvanski spreg. Me|utim, ako se za mre`icu ve`e

galvanski spreg (za odre|ivanje pH rastvora) i mre`ica pove`e tako

da joj se saop{ti negativan potencijal, do}i }e do ko~enja elektrona.

To }e dovesti do smanjenja anodne struje. Ovo smanjenje srazmer-

no je elektromotornoj sili galvanskog sprega

EMS

, koja zavisi od

potencijala indikatorske elektrode, odnosno od pH rastvora. Skala

mernog instrumenta izra`ena je posebno u

jedinicama, {to

zna~i da se direktno mogu pro~itati i elektromotorna sila galvanskog

sprega i pH vrednost analiziranog rastvora. Na savremenim digital-

nim aparatima ova vrednost se o~itava na elektronskom prikaziva~u

– displeju.

Medenica / Male{ev

146

Slika 4.

Shema pH-metra

B – izvor jednosmerne struje

– izvor struje za katodu

EMS

– galvanski spreg

k – katoda

a – anoda

M – mre`ica

A – ampermetar

Eksperimentalna fizi~ka hemija

147

Aparatura i hemikalije

pH-metar MA 5740 I

SKRA

– Kranj (slike 5 i 6)

Kombinovana elektroda

Pufer

Analizirani rastvor

URADITE SAMOSTALNO ...

Merenje

H rastvora

H-metrom

Zadatak eksperimenta

Izmeriti pH rastvora pH-metrom.

Slika 5.

pH-metar MA 5740 I

SKRA

– Kranj

Pritiskom na tipku

na prikaziva~u se javlja vrednost 0,000.

Ispisati vrednost pufera kojim se vr{i kalibracija, ~ime se otklanja

uticaj potencijala asimetrije i pritisnuti tipku

enter

. Na prikaziva~u

se javlja pribli`na vrednost pufera. Kada se broj stabilizuje, ponovo

pritisnuti

enter

. Ako je kalibracija zavr{ena, ~uje se zvu~ni signal

kao dug i kratak pisak. Gase se diode

cal

1 i pH. U protivnom, po-

javljuje se natpis

Err

i kodni broj gre{ke. Gre{ke se otklanjaju prema

uputstvu proizvo|a~a koje sadr`i spisak kodnih brojeva gre{aka.

Kalibracija u dve ta~ke

vr{i se pomo}u dva pufera, a izbor pufera

je takav da jedan pufer treba da ima manju pH vrednost, a drugi ve-

}u od o~ekivane pH vrednosti analiziranog rastvora. Kalibracija u

drugoj ta~ki mo`e se izvr{iti samo nakon izvr{ene kalibracije u prvoj

ta~ki.

Kombinovanu elektrodu spustiti u rastvor drugog pufera poz-

natog pH i pritisnuti

cal

2 (kalibracija u drugoj ta~ki) i

temp

. Na

prikaziva~u se javlja vrednost temperature od 25°C. Ako je potreb-

no, ispisati novu vrednost temperature prema temperaturi pufera i

pritisnuti tipku

enter

. Gasi se dioda

temp

Pritiskom na tipku

na prikaziva~u se javlja vrednost prethod-

nog pufera kojim je vr{ena kalibracija u jednoj ta~ki. Ispisati novu

vrednost pufera kojim se vr{i kalibracija u drugoj ta~ki, a zatim pri-

tisnuti tipku

ENTER

. Na prikaziva~u se javlja pribli`na vrednost pufe-

ra. Kada se broj stabilizuje, ponovo pritisnuti

enter

. Ako je kalibra-

cija zavr{ena, ~uje se zvu~ni signal kao dug i kratak pisak. Gase se

diode

cal

1 i pH. U protivnom pojavljuje se natpis

Err

i kodni broj

gre{ke. Radi otklanjanja gre{ke postupa se prema uputstvu proizvo-

|a~a koje sadr`i spisak kodnih brojeva gre{aka.

Merenje pH rastvora

Elektrodu izvaditi iz pufera, isprati destilovanom vodom, a zatim

osu{iti upijanjem filtar-hartijom, bez pritiskanja staklene mem-

brane. Elektrodu potopiti u rastvor ~iji se pH odre|uje i pritisnuti

funkcijsku tipku

. Na prikaziva~u se javlja vrednost pH rastvora,

koja se ubrzo stabilizuje.

PA@NJA:

Pri radu sa staklenom ili kombinovanom elektrodom treba biti veo-

ma pa`ljiv, jer je staklena membrana u kru{kastom delu lako lomljiva.

Eksperimentalna fizi~ka hemija

149

Medenica / Male{ev

150

REZULTATI

Tabela 1.

Rezultati merenja na pH metru

PUFERA

ANALIZIRANOG RASTVORA

Za odre|ivanje F

–

jona koristi se membrana od monokristala

LaF

, a za odre|ivanje S

2–

jona membrana od presovanog Ag

Danas je razvijen veliki broj jon-selektivnih membrana za odre-

|ivanje niza katjona i anjona.

Membrane od te{ko rastvornih soli mogu se primeniti kada u

kristalu soli postoji neka mobilna jonska vrsta koja mo`e da prenosi

naelektrisanje. Provo|enje omogu}ava postojanje defekata u kristal-

noj strukturi i pojavu »upra`njenih mesta«, kroz koja se mogu kre-

tati samo joni odre|enih karakteristika, dok ostali joni ne mogu uti-

cati na provodljivost membrane. Na primer, Ag

jon je mobilan u

solima Ag

S i AgX, dok je kod LaF

mobilan F

–

jon, a LaF

jon je

~vrsto vezan u re{etki.

Kao unutra{nja referentna elektroda naj~e{}e se koristi elektroda

druge vrste, Ag



AgCl, Cl

–

, i u tom slu~aju unutra{nji elektrolit tre-

ba da sadr`i korespondentne jone unutra{nje referentne elektrode i

jonske vrste u membrani. Na primer, unutra{nji elektrolit bromidne

elektrode sadr`i Cl

–

i Br

–

jone, a kod fluoridne elektrode to su Cl

–

joni.

Fluoridna

monokristalna jon-selektivna elektroda prikazuje se

na slede}i na~in:



AgCl, Cl

–

), F

–

)



LaF

Kako je aktivnost F- jona u unutra{njem elektrolitu poznata i

konstantna, potencijal fluoridne elektrode zavisi samo od aktivnosti

fluoridnih jona u spolja{njem, merenom rastvoru:

Jodidna

jon-selektivna elektroda prikazuje se na slede}i na~in:



AgCl, Cl

–

), J

–

)



AgJ

Izraz za potencijal jodidne jon-selektivne elektrode izvodi se na

isti na~in kao i izraz za potencijal kalomelove elektrode (str 128),

tako da kona~ni izraz glasi:

Medenica / Male{ev

152

E = E

–

(1)

E = E

–

(2)

Staklena elektroda, koja je opisana u poglavlju »Merenje pH rast-

vora pH-metrom« str 143, pripada grupi jon-selektivnih elektroda

sa ~vrstom membranom.

Jon-selektivne elektrode sa nekristalnom membranom

Membrane ovih elektroda napravljene su obi~no od porozne plas-

ti~ne mase, sinterovanog stakla ili nekog drugog inertnog poroznog

materijala natopljenog rastvara~em ili te~no{}u koja je nerastvorna

u vodi. Za gra|enje te~nih membrana naj~e{}e se koriste jonski iz-

menjiva~i, elektroneutralna makrocikli~na jedinjenja, kvaternerne

amonijum soli i dr.

Detaljniji opisi ovih elektroda mogu se na}i u specijalizovanoj

literaturi o jon-selektivnim elektrodama.

Ekspanzija primene jon-selektivnih elektroda, a u novije vreme i

potenciometrijskih biosenzora, pove}ava mogu}nost kori{}enja po-

tenciometrije u farmaceutskim istra`ivanjima. Danas se ne mo`e za-

misliti instrumentalna laboratorija bez jon-selektivnih elektroda.

Jednostavnost rukovanja, velika osetljivost i preciznost ovih elektro-

da doprinela je njihovoj sve ~e{}oj i {iroj upotrebi. U farmaceutskim

laboratorijama koristi se u kontroli kvaliteta lekova i `ivotnih na-

mirnica, u farmaceutsko-tehnolo{kim istra`ivanjima, toksikolo{koj

hemiji, a u novije vreme i u biohemiji.

Eksperimentalna fizi~ka hemija

153

Eksperimentalna fizi~ka hemija

155

Priprema rastvora

Napraviti 25 mL 1,0 mol L

-1

osnovnog rastvora kalijum-jodida. Od

ovog rastvora (c

) napraviti tri rastvora zadatih koncentracija (c

Koriste}i izraz:

izra~unati zapremine V

osnovnog rastvora, koji se odmerava u od-

merne sudove od 50 mL da bi se napravili rastvori zadatih koncen-

tracija. U ove rastvore kalijum-jodida dodati toliku zapreminu kali-

jum-nitrata (1,0 mol L

-1)

da jonska ja~ina (I) u svim rastvorima

bude 0,5. Odmerne sudove dopuniti destilovanom vodom do oz-

nake.

Slika 2.

pH-metar

Radiometer

28 – Copenhagen

1 – glavni prekida~

2 – potenciometar za kalibraciju skale

instrumenta

3 – preklopnik za podru~ja pH/mV

4 – potenciometar za pode{avanje

temperature

5 – skala

6 – jon-selektivna elektroda

7 – kalomelova elektroda

= c

(3)

Jonsku ja~inu izra~unati iz slede}eg izraza:

gde je:

I – jonska ja~ina

c – koncentracija (katjona K ili anjona A)

z – naelektrisanje (katjona ili anjona).

Merenje na pH-metru

Na pH-metru izabrati odgovaraju}u skalu u mV. Sipati ispitivani

rastvor u ~a{u i u rastvor uroniti referentnu kalomelovu i jodidnu

jon-selektivnu elektrodu.

Elektromotorna sila dobijenog sprega predstavlja razliku poten-

cijala jodidne jon-selektivne i kalomelove elektrode:

gde je:

Ag/AgJ, J

–

– potencijal jodidne elektrode:

Medenica / Male{ev

156

....... mL 1,0 mol L

-1

....... mL 1,0 mol L

-1

KNO

(I = 0,5)

dopuniti do 50 mL destilovanom vodom

....... mL 1,0 mol L

-1

....... mL 1,0 mol L

-1

KNO

(I = 0,5)

dopuniti do 50 mL destilovanom vodom

....... mL 1,0 mol L

-1

....... mL 1,0 mol L

-1

KNO

(I = 0,5)

dopuniti do 50 mL destilovanom vodom

Br.

c KCl (mol L

-1

)

Odmeriti

I =

. z

(

. z

+ c

. z

...)

(4)

EMS = E

Ag/AgJ, J–

– E

kal

(5)

Medenica / Male{ev

158

kal

= 245 mV

REZULTATI

Tabela 1.

Kalibraciona kriva E = f(log c)

c KJ (mol L

-1

)

log c

< >

EMS (mV)

< >

EMS

(mV)

E (mV)

(mV)

(mol L

-1

)

(mV)

RT/F

Grafi~ka

vrednost

RT/F

Teorijska

vrednost

Tabela 2.

Rezultati

Eksperimentalna fizi~ka hemija

159

Potenciometrijska titracija

je kvantitativna elektrohemijska meto-

da za odre|ivanje koncentracije rastvora. Kraj titracije se odre|uje

na osnovu promene potencijala indikatorske elektrode u zavr{noj

ta~ki titracije. Potenciometrijska titracija dobila je ime po tome {to

potencijal elektrode predstavlja indikator zavr{ne ta~ke titracije. Up-

ravo zbog toga je i elektroda, koja ima ulogu indikatora, nazvana in-

dikatorska, jer menja svoj potencijal u zavisnosti od aktiviteta ka-

rakteristi~nih jona u rastvoru. Ova metoda daje ta~nije rezultate od

volumetrijske, a mo`e se koristiti i kod titracija veoma razbla`enih

rastvora, mutnih i obojenih, ili u slu~aju kada ne postoji odgovara-

ju}i indikator. Pored analiti~ke primene, potenciometrijska titracija

se koristi i za odre|ivanje nekih karakteristi~nih veli~ina, kao {to su

konstante protolize kiselina i baza, konstante stabilnosti kompleksa,

proizvod rastvorljivosti i standardni oksidoredukcioni potencijali.

U osnovi potenciometrijske titracije le`e dva procesa uslovljena

jedan drugim. Prvi je hemijski, tj. poznata hemijska reakcija koja na-

staje izme|u analiziranog rastvora i titranta. Drugi je fizi~kohemij-

ski proces, odnosno promena potencijala elektrode kao posledica

hemijske reakcije. Na osnovu ove povezanosti mo`e se pratiti odvi-

janje hemijske reakcije nekog titracionog sistema zahvaljuju}i pro-

meni potencijala indikatorske elektrode.

Potenciometrijska titracija mo`e se izvoditi tako {to se milivolt-

metrom sa velikom otporno{}u meri promena elektromotorne sile

galvanskog sprega, koji se sastoji od analiziranog rastvora (titranda),

referentne i odgovaraju}e indikatorske elektrode. Izbor indikatorske

elektrode zavisi od vrste hemijske reakcije (neutralizacija, talo`enje

ili precipitacija, stvaranje kompleksa i oksidoredukcija) u titracio-

nom sistemu. O izboru odgovaraju}e indikatorske elektrode bi}e re~i

na narednim stranicama ovog ud`benika, kod konkretnih primera.

Kako je potencijal referentne elektrode konstantan, to elektromo-

torna sila zavisi samo od potencijala indikatorske elektrode. Na ovaj

na~in mogu}e je, merenjem promene elektromotorne sile u toku tit-

racije, odrediti zapreminu titranta poznate koncentracije po zavr-

{etku stehiometrijske reakcije izme|u analiziranog rastvora i titranta,

a iz toga izra~unati koncentraciju analiziranog rastvora. U po~etku

titracije elektromotorna sila se neznatno menja, dok je u blizini za-

vr{ne ta~ke titracije ta promena najve}a.

POTENCIOMETRIJSKA TITRACIJA

Teorijski princip

* prira{taj zapremine titranta

** izra~unava se kao koli~nik razlike potencijala dva susedna mere-

nja (

∆

E) i razlike odgovaraju}ih zapremina (

∆

[

npr. (86-84)/(0,2-0), zatim (88-86)/(0,4-0,2) itd.

]

Drugi izvod se izra~unava na isti na~in kao prvi izvod, odnosno

kao »prvi izvod prvog izvoda«.

Prvi, drugi i ostali izvodi ta~no se izra~unavaju interpolacijom

polinoma, {to podrazumeva odre|ene matemati~ke postupke, a koji

su danas sastavni deo mnogih programa za obradu rezultata.

Upotreba potenciometrijskih titracija je veoma {iroka u labora-

torijskim istra`ivanjima pri razli~itim hemijskim reakcijama. Kori-

ste se u svim oblastima farmaceutskih nauka, a neke potenciometrij-

ske titracije su oficinalne u pojedinim farmakopejama.

Eksperimentalna fizi~ka hemija

161

Tabela 1.

Primer izra~unavanja

prvog izvoda krive

Integralna kriva

Prvi izvod

V (mL)

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

E(mV)

142

342

360

376

388

398

∆

V**

220

1000

V(mL)*

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

Eksperimentalna fizi~ka hemija

163

Potenciometrijska titracija pri reakciji neutralizacije (pH-metrijska

titracija) zasniva se na pra}enju promene potencijala elektrode oset-

ljive na promenu pH rastvora u toku titracije, odnosno merenju

elektromotorne sile sprega pH indikatorske i referentne elektrode,

uronjene u rastvor koji se titruje. Kao indikatorska elektroda koristi

se bilo koja elektroda osetljiva na promenu pH, a najjednostavnija

za rad je staklena, ~iji je potencijal prikazan izrazom (3) na str 144.

Kao referentna elektroda, naj~e{}e se koristi kalomelova, a njen po-

tencijal dat je izrazom (14) na str 129.

Promena pH titrovanog rastvora ili elektromotorne sile galvan-

skog sprega u toku titracije prati se na milivoltmetru ili pH-metru.

Mogu}e je titrovati i sme{u kiselina ili baza, ali samo pod uslo-

vom da je razlika njihovih konstanti protoliza dovoljno velika. U

tom slu~aju dobija se potenciometrijska titraciona kriva sa jasno de-

finisanim ta~kama infleksije, pa je mogu}e precizno odrediti zavr{-

nu ta~ku titracije svake pojedina~ne kiseline ili baze.

Reakcija neutralizacije

Teorijski princip

ku mernog instrumenta ta~no na vrednost pH pufera (polo`aj ovog

potenciometra ne menjati u toku rada). Posle zavr{ene kalibracije,

pritiskom na prekida~ sa oznakom

std by

(sa~ekati) kazaljku mer-

nog instrumenta vratiti u nulti polo`aj.

Ovim postupkom posti`e se kompenzacija potencijala asimetrije

staklene elektrode.

Postupak

U biretu sipati rastvor titranta (hloridna kiselina). U ~a{u sipati pi-

petom ta~no odmerenu zadatu zapreminu rastvora natrijum-hidro-

ksida i toliku koli~inu vode, da se omogu}i rad magnetne me{alice i

pravilno uranjanje elektroda.

Uklju~iti magnetnu me{alicu i podesiti rad na 800 obrtaja u mi-

nuti. U rastvor pa`ljivo uroniti staklenu i kalomelovu elektrodu.

Preklopnik sa oznakom

range

postaviti na odgovaraju}e podru~je

pH vrednosti. Pritiskom na prekida~ sa oznakom

read

pro~itati

vrednost pH na skali, a zatim kazaljku instrumenta vratiti na nulu

skale pritiskom na prekida~

std by

Preklopnikom

range

izabrati odgovaraju}e podru~je za merenje

elektromotorne sile i pro~itati vrednost EMS u mV.

Titrant dodavati u inkrementima od 0,2 mL i o~itavati vrednosti

pH i elektromotorne sile (EMS), kada se igla mernog instrumenta

ustali. Nagla promena pH, odnosno EMS ukazuje na postignutu za-

vr{nu ta~ku titracije. Posle nagle promene izvr{iti jo{ desetak me-

renja.

Iz dobijenih vrednosti EMS izra~unati potencijal staklene elek-

trode E i konstruisati grafike funkcija E = f(V) i

∆

V = f(V). Od-

rediti zavr{nu ta~ku titracije i izra~unati koncentraciju rastvora ti-

tranda.

Grafi~ki prikazati Nernstovu jedna~inu za potencijal staklene

elektrode E = E

– 0,0591 pH, odrediti konstantni potencijal E

dobijeni nagib prave uporediti sa teorijskim.

Rezultate prikazati tabelarno i grafi~ki.

Eksperimentalna fizi~ka hemija

165

Medenica / Male{ev

166

V HCl (mL)

EMS (mV)

E (mV)

Prvi izvod

V (mL)

∆

E /

∆

REZULTATI

Tabela 1.

Potenciometrijska titracija natrijum-hidroksida

sa hloridnom kiselinom

E = 244,4 mV (zasi}ena kalomelova elektroda) na t = 20°C

Eksperimentalna fizi~ka hemija

169

Potenciometrijskim titracijama mogu se pratiti i talo`ne reakcije u

kojima je proizvod reakcije te{ko rastvorljivo jedinjenje. Posledica

toga je smanjenje koncentracije karakteristi~nih jona u rastvoru na

koje indikatorska elektroda reaguje, odnosno promena potencijala

indikatorske elektrode.

Srebro-nitrat se naj~e{}e koristi kao titrant za odre|ivanje halo-

genida, merkaptana, sulfida, arsenata, fosfata i oksalata. U tom slu~aju

kao indikatorska elektroda koristi se ili srebrova ili jon-selektivna

srebro-sulfidna elektroda. Referentna kalomelova elektroda mora

biti elektroliti~ki odvojena od indikatorske elektrode zbog prisutnog

–

jona u elektrolitu same elektrode. Tada se koristi most od agar-

agara uz dodatak kalijum-nitrata ili umesto klasi~ne kalomelove

elektrode koja sadr`i merkuro-hlorid i kalijum-hlorid, elektroda

koja sadr`i merkuro-sulfat i elektrolit kalijum-sulfat, odnosno mer-

kuro-sulfatna elektroda.

Potencijal indikatorske srebrove elektrode dat je slede}im Nern-

stovim izrazom:

Reakcija talo`enja

Teorijski princip

Ag+/Ag

= E

Ag+/Ag

Ag+

(1)

Aparatura i hemikalije

pH-metar MA 5703

Iskra

– Kranj (slika 1)

Srebrova elektroda P4011

Kalomelova elektroda K401

Mehani~ka me{alica

Elektroliti~ki most od agar-agara sa dodatkom

amonijum-nitrata

Srebro-nitrat

Kalijum-hlorid

Priprema

Pripremiti biretu sa rastvorom kalijum-hlorida.

U ~a{u sipati destilovanu vodu i ta~no odmerenu zapreminu

rastvora srebro-nitrata. Uroniti elektrodu od srebra i me{alicu.

Anodni prostor (srebrova elektroda / srebro-nitrat) i katodni

(kalomelova elektroda / kalijum-hlorid) povezati mostom od agar-

agara, napravljenog sa amonijum-nitratom. Tako je pripremljen gal-

vanski spreg, ~ija se elektromotorna sila mo`e meriti.

U analizirani rastvor spustiti me{alicu i pomo}u promenljivog

otpornika podesiti optimalan rad me{alice, tako da se ostvari mirno

me{anje rastvora.

Medenica / Male{ev

170

URADITE SAMOSTALNO ...

Potenciometrijska
titracija
talo`ne reakcije
pomo}u pH-metra

Zadatak eksperimenta

Izvr{iti dve titracije zadate zapremine rastvora srebro-nitrata sa

kalijum-hloridom.

Vrednosti dobijene drugom titracijom prikazati grafi~ki kao

funkciju EMS = f(V).

Odrediti zavr{nu ta~ku titracije grafi~kim putem i izra~unati

broj grama srebra (m) u zadatoj zapremini srebro-nitrata.

Medenica / Male{ev

172

Grafi~ki prikazati funkciju EMS = f(V) i

∆

EMS/

∆

V = f(V) za

drugu titraciju, odrediti zavr{nu ta~ku titracije iz prvog izvoda i iz-

ra~unati broj grama srebra (

) u zadatoj zapremini srebro-nitrata.

Primer za izra~unavanje prvog izvoda dat je na strani 161.

Rezultate prikazati tabelarno i grafi~ki.

Eksperimentalna fizi~ka hemija

173

V KCl (mL)

EMS (mV)

V KCl (mL)

EMS (mV)

V KCl (mL)

∆

EMS /

∆

I titracija

II titracija

Prvi izvod

REZULTATI

Tabela 1

Potenciometrijske titracije EMS = f(V)

Tabela 2.

Rezultati

V AgNO

(mL)

c KCl (mol L

-1

)

V KCl

u Z.T.T. (mL)

m Ag (g)

Aparatura i hemikalije

Ure|aj za izvo|enje Pogendorfove metode (slika 1, strana 131)

Srebrova i kalomelova elektroda

Mehani~ka me{alica

Elektroliti~ki most od agar-agara

Srebro-nitrat

Kalijum-hlorid

Priprema

Prema shemi za Pogendorfovu metodu kompenzacije, prikazanoj na

slici 1 (strana 131), obrazovati strujno kolo za odre|ivanje elektro-

motorne sile.

Biretu pripremiti sa standardnim rastvorom kalijum-hlorida. U

~a{u sipati destilovanu vodu i zadatu zapreminu srebro-nitrata od-

merenu pipetom. Uroniti srebrovu i kalomelovu elektrodu i uklju-

~iti me{alicu, tako da se ostvari mirno me{anje rastvora.

Postupak

Kratkim uklju~ivanjem tastera i pomeranjem kliznog kontakta na}i

polo`aj na otporniku kada igla na galvanometru miruje (I = 0). Ovaj

odse~ak, na mostu, izra`en u milimetrima, odrediti prvo za ~ist rastvor

srebro-nitrata. Dodavati kalijum-hlorid u inkrementima od 0,2 mL

i posle svakog dodatka odrediti odse~ak kojim se vr{i kompenzacija.

Posle nagle promene vrednosti odse~ka izvr{iti jo{ toliko merenja da

se dobije pogodna integralna kriva za odre|ivanje zavr{ne ta~ke ti-

Medenica / Male{ev

176

URADITE SAMOSTALNO ...

Potenciometrijska
titracija talo`ne
reakcije po
Pogendorfovoj
metodi kompenzacije

Zadatak eksperimenta

Izvr{iti dve titracije zadate zapremine rastvora srebro-nitrata sa

kalijum-hloridom.

Vrednosti dobijene drugom titracijom prikazati grafi~ki kao

funkciju a = f(V). Odrediti zavr{nu ta~ku titracije grafi~kim putem

i izra~unati masu srebra (m) u zadatoj zapremini srebro-nitrata.

tracije. Izvesna mala vrednost EMS sprega, odnosno vrednost od-

se~ka, ukazuje da u rastvoru postoji mala koncentracija jona srebra,

uslovljena proizvodom rastvorljivosti srebro-hlorida.

Titraciju ponoviti jo{ jednom sa istom zapreminom rastvora sre-

bro-nitrata uz dodatak manjih inkremenata titranta.

Iz druge titracije konstruisati grafike funkcija:

a = f(V), i

∆

V = f(V)

Odrediti zavr{nu ta~ku titracije iz prvog izvoda i izra~unati masu

srebra u odmerenoj zapremini srebro-nitrata. Primer za izra~una-

vanje prvog izvoda dat je na strani 161.

Rezultate prikazati tabelarno i grafi~ki.

Eksperimentalna fizi~ka hemija

177

Eksperimentalna fizi~ka hemija

179

Tabela 2.

Rezultati

V AgNO

(mL)

c KCl (mol L

-1

)

V KCl

u Z.T.T. (mL)

m Ag (g)

Eksperimentalna fizi~ka hemija

181

Potenciometrijskim titracijama se odre|uju koncentracije supstan-

cija u rastvorima u kojima se odigravaju i oksidoredukcioni hemij-

ski procesi sa titrantom. Oksidovani i redukovani oblik nekog jona

~ine oksidoredukcioni sistem ili, kra}e, redoks sistem.

Ox + ne

–

Red

U toku titracije stvaraju se dva redoks sistema, supstancije koja se

titruje (titrand) i supstancije kojom se titruje (titrant). Prva postoji

do postizanja ta~ke ekvivalencije, a druga posle nje. Potencijal in-

dikatorske elektrode u rastvoru definisan je prisutnim redoks siste-

mom i prikazan op{tim Nernstovim izrazom:

Kao indikatorska elektroda koristi se elektroda od zlata ili plati-

ne, jer hemijski ne reaguje u redoks sistemu i brzo uspostavljaju rav-

note`ni potencijal u zavisnosti od odnosa oksidovanog i redukova-

nog oblika jona.

Do zavr{ne ta~ke titracije potencijal indikatorske elektrode defi-

ni{e redoks sistem rastvora koji se titruje. Posle zavr{ne ta~ke titraci-

je, potencijal indikatorske elektrode definisan je redoks sistemom

koji poti~e od titranta.

Odre|ivanje zavr{ne ta~ke titracije utoliko je ta~nije ukoliko se

potencijali ova dva redoks sistema vi{e razlikuju.

Reakcija oksidoredukcije

Teorijski princip

E = E

red

(1)

kati da se rastvor dobro izme{a, odnosno da se izvr{i hemijska reak-

cija:

U toku ove oksidoredukcione titracije stvaraju se dva redoks si-

stema koji defini{u potencijal elektrode:

+ e

–

= 0,771 V

MnO

–

+ 5e

–

+ 8H

+ 4H

=1,510 V

Eksperimentalna fizi~ka hemija

183

Slika 1.

pH-meter

Radiometer

22 – Copenhagen

1 – glavni prekida~

2 – preklopnik »1«

3 – preklopnik »2« (pH/mV)

4 – potenciometar za pode{avanje

temperature

5 – skala

6 – priklju~ak indikatorske elektrode

7 – kalomelova elektroda

10 FeSO

+ 2KMnO

+ 8H

5Fe(SO

)

+ 2MnSO

+ K

+ 8H

Medenica / Male{ev

184

Pri izboru titranta vodi se ra~una da se standardni potencijali

oba sistema dovoljno razlikuju, da bi se dobila integralna potencio-

metrijska kriva sa jasno definisanom ta~kom infleksije.

Postupak

Proveriti da li se preklopnik »2« nalazi na polo`aju »×1«. Preklopnik

»1« okrenuti udesno na »+ mV«, sa~ekati da se kazaljka umiri i na

skali pro~itati vrednost EMS u mV. Preklopnik »1« vratiti na po~et-

nu poziciju, dodati 0,5 mL rastvora kalijum-permanganata iz birete,

sa~ekati da se rastvor izme{a, tj. da se reakcija stehiometrijski izvr{i i

ponovo pro~itati vrednost EMS na skali. Merenja vr{iti dodavanjem

istih zapremina od 0,5 mL titranta sve dok se ne javi nagli skok EMS.

Kad kazaljka iza|e van opsega skale, preklopnik »2« prebaciti na oz-

naku »+ 500 mV« (na taj na~in se skala ekspandira za 500 mV). Tada

se kazaljka vrati na skalu, a pro~itana vrednost EMS u mV se sabere

sa 500 mV i unese u tabelu. Posle naglog skoka izvr{iti jo{ 4–5 me-

renja, ~ime je titracija zavr{ena.

Do zavr{ne ta~ke titracije potencijal elektrode defini{e odnos

koncentracija Fe

/ Fe

, a posle zavr{ne ta~ke odnos koncentracija

/ Mn

(MnO

–

/ Mn

Drugu titraciju uraditi preciznije, dodaju}i manje inkremente ti-

tranta, kako bi se dobila kriva pogodna za ta~no odre|ivanje zavr{ne

ta~ke titracije.

Iz tabele za drugu titraciju izra~unati prvi izvod i grafi~kim

putem prikazati integralnu krivu EMS = f(V) i krivu prvog izvoda

∆

EMS/

∆

V = f(V). Odrediti zavr{nu ta~ku titracije i izra~unati kon-

centraciju rastvora gvo`|e(II)-sulfata.

Primer za izra~unavanje prvog izvoda dat je na strani 161.

Rezultate prikazati tabelarno i grafi~ki.

Medenica / Male{ev

186

Tabela 2.

Rezultati

V FeSO

(mL)

c KMnO

(mol L

-1

)

V KMnO

u Z.T.T. (mL)

c FeSO

(mol L

-1

)

(8)

Provodljivost

MERENJE PROVODLJIVOSTI

(KONDUKTOMETRIJA)

Odre|ivanje specifi~ne i molarne

provodljivosti jakih elektrolita

KONDUKTOMETRIJSKA TITRACIJA

Odre|ivanje koncentracije natrijum-hidroksida

Odre|ivanje koncentracije sir}etne kiseline

Specifi~na provodljivost

predstavlja provodljivost rastvora elek-

trolita u posudi oblika kocke stranica 1 m, na ~ijim se suprotnim

stranama nalaze elektrode na rastojanju od 1 m. Jedinice za speci-

fi~nu provodljivost su

Ω

–1

, odnosno S . m

–1

Iz jedna~ina (3) i (5) sledi:

Odnos

/A (gde je

– rastojanje izme|u elektroda, a A – povr{ina

elektrode) defini{e tzv.

konstantu konduktometrijske }elije k

(ra-

niji naziv kapacitet posudice):

Ova veli~ina mora ostati nepromenjena u toku merenja, pa se

elektrode moraju nalaziti na stalnom rastojanju. Ovako definisana

konstanta konduktometrijske }elije va`ila bi samo u slu~aju kada bi

elektrode bile zidovi suda. Me|utim, kako to nije slu~aj, linije sila

elektri~nog polja se razilaze (slika 1), pa rastojanje i povr{ina elek-

troda nisu ta~no definisani.

Zato je neophodno

konstantu }elije k

odrediti eksperimentalno

pri prvoj upotrebi, tako {to se meri otpornost rastvora, npr. KCl

poznate koncentracije, ~ija se vrednost specifi~ne provodljivosti na

radnoj temperaturi mo`e na}i tabelarno (tablica 8 u Prilogu). Ovaj

postupak naziva se kalibracija konduktometrijske }elije. Vrednost

konstante k

bi}e nepromenjena sve dok me|usobno rastojanje i fi-

zi~ko stanje elektroda ostanu nepromenjeni. Elektrode su od platine

ili platinirane platine, ~ime se pove}ava efektivna povr{ina elektrode.

Specifi~na provodljivost zavisi od:

prirode elektrolita i polarnosti rastvara~a,

temperature,

koncentracije.

Sa pove}anjem temperature opada viskoznost rastvora, a rastu

brzina kretanja jona i provodljivost. Eksperimentalno je utvr|eno

da sa porastom temperature za 1°C provodljivost raste prose~no za

2%, pa je usled toga neophodno konduktometrijska merenja vr{iti u

termostatu pri konstantnoj temperaturi.

Sa porastom koncentracije, pri konstantnoj temperaturi, pro-

vodljivost u po~etku raste do odre|ene granice, jer se dodatkom

Medenica / Male{ev

190

(6)

(7)

Slika 1.

Linije sila elektri~nog polja

izme|u elektroda

elektrolita pove}ava broj jona u rastvoru (slika 2). Pri ve}im koncen-

tracijama elektrolita, provodljivost po~inje da opada. To se obja{nja-

va smanjenjem koncentracije rastvara~a u odnosu na elektrolit, {to

ima za posledica smanjenje stepena disocijacije (protolize), pove-

}anje me|ujonskih sila i stvaranje jonskih asocijata.

Specifi~na provodljivost, odnosno otpor elektrolita meri se me-

todom

Vitstonovog

(Wheatston),

mosta

. Shema ure|aja prikazana

je na slici 3.

Za odre|ivanje provodljivosti elektrolita koristi se niskonapon

ski (desetak volti) izvor naizmeni~ne struje velike frekvencije (~ak i

nekoliko hiljada Hz). U suprotnom, pri prolasku jednosmerne stru-

je kroz elektrolit do{lo bi do elektrohemijske promene elektrolita,

odnosno do promene ne samo koncentracije, ve} i sastava elektroli-

ta. Za dobijanje naizmeni~ne struje koristi se elektronski oscilator

koji je vezan za krajeve otpornika AB.

Kao indikator instrument mo`e se koristiti telefonska slu{alica,

magi~no oko ili osetljiv galvanometar za merenje naizmeni~ne stru-

je. On slu`i kao detektor bestrujnosti u delu kola D – C, tj. kada je

pomeranjem kliznog kontakta D izvr{eno uravnote`enje mosta. Ta-

da je:

su nepoznati otpori i mogu se izraziti du`inama `ica

, od-

nosno

Eksperimentalna fizi~ka hemija

191

Slika 2.

Zavisnost specifi~ne provodljivosti

od koncentracije

Slika 3.

Shema Vitstonovog mosta

S – izvor naizmeni~ne struje

AB – otpornik

C – trojna ta~ka

D – klizni kontakt

T – indikator instrument

– nepoznati otpor (elektrolit)

R – otporna dekada

: R = R

: R

(8)

: R

= a : b

(9)

Eksperimentalna fizi~ka hemija

193

Molarna provodljivost zavisi od:

prirode elektrolita i rastvara~a,

razbla`enja,

temperature.

Molarna provodljivost nekog binarnog elektrolita predstavlja

funkciju stepena protolize ili disocijacije (

) i molarnih jonskih

provodljivosti katjona (

) i anjona (

–

Kako se molarna provodljivost menja sa razbla`enjem prikazano

je na slici 4.

Slabi elektroliti nisu u potpunosti disosovani (

< 1), a jaki elek-

troliti su potpuno disosovani na jone (

= 1). Kod slabih elektrolita

(CH

COOH) provodljivost linearno raste, jer sa razbla`enjem raste

i stepen protolize. Ukoliko je stepen protolize ve}i u rastvoru je pri-

sutno vi{e jona, pa je i provodljivost ve}a. Kod jakih elektrolita (HCl)

molarna provodljivost pri malim razbla`enjima je relativno mala, a

sa pove}anjem razbla`enja naglo raste i dosti`e konstantnu vred-

nost, koja se daljim razbla`enjem ne menja. Ova grani~na vrednost

naziva se

molarna provodljivost pri beskona~nom razbla`enju

ili

∞

. To je konstantna veli~ina za svaki elektrolit na datoj tempera-

turi i predstavlja provodljivost rastvora kada koncentracija te`i nuli,

odnosno kada je razbla`enje

jako veliko.

Prema jedna~ini (16), molarna provodljivost pri beskona~nom

razbla`enju jednaka je zbiru molarnih jonskih provodljivosti pri

beskona~nom razbla`enju:

Molarne jonske provodljivosti

pri beskona~nom razbla`enju su

karakteristi~ne vrednosti na datoj temperaturi (tablica 9 u Prilogu).

(

–

)

(16)

–

(18)

= lim

(17)

Slika 4.

Zavisnost molarne provodljivosti

od razbla`enja

Medenica / Male{ev

194

Molarna provodljivost pri beskona~nom razbla`enju jakih elek-

trolita mo`e se odrediti grafi~kim putem iz

Kolrau{ovog

(Kohl-

rausch) empirijskog

zakona kvadratnog korena

gde su

empirijske konstante za svaki elektrolit.

Ako c

0, onda i

√

0, pa sledi da je a =

odnosno:

Ovo zna~i da Kolrau{ov zakon kvadratnog korena predstavlja

jedna~inu prave koja se grafi~ki prikazuje kao na slici 5.

Konstanta

mo`e se odrediti kao tangens ugla prave:

odnosno:

Za slabe elektrolite

ne mo`e se grafi~kim putem odrediti .

Iz molarne provodljivosti mogu se odrediti prenosni brojevi

katjona i anjona, kao i va`ni fizi~kohemijski parametri – stepen pro-

tolize, konstanta protolize i proizvod rastvorljivosti te{ko rastvorne

soli.

Prema jedna~inama (16) i (18)

stepen protolize

dat je izrazom:

Iz molarne provodljivosti i stepena protolize mo`e se izra~unati i

konstanta protolize. Slabi elektroliti u rastvorima ne disosuju pot-

puno (

<1), ve} postoji ravnote`a izme|u molekula i jona.

a – b

√

(19)

– b

√

(20)

Slika 5.

Grafi~ki prikaz Kolrau{ovog zakona

kvadratnog korena

b =

–

√

–

√

(21)

b =

= tg

∆Λ

∆√

(22)

(23)

+ A

–

(24)

Aparatura i hemikalije

Konduktometar MA 5962

Iskra

– Kranj (slika 6)

Konduktometrijska }elija

Termostat

Rastvor kalijum-hlorida

Na prikazanom konduktometru skala je ba`darena u jedinicama ot-

pora, a indikator instrument je osetljiv instrument sa kazaljkom.

Pored toga, indikator instrument mo`e biti i magi~no oko.

Kalibracija konduktometrijske }elije

Ovaj postupak podrazumeva odre|ivanje konstante

, koja pred-

stavlja odnos rastojanja

izme|u elektroda i povr{ine elektrode

Odre|ivanje se vr{i merenjem otpornosti rastvora KCl poznate kon-

centracije, za koji se vrednost specifi~ne provodljivosti

, na radnoj

temperaturi, nalazi u tablici 8 u Prilogu.

Priprema

U posudu za konduktometriju sipati malo rastvora elektrolita ~ija se

provodljivost odre|uje i isprati elektrode. Isprazniti posudu, a zatim

sipati rastvor i staviti posudu u termostat.

Elektrode celom povr{inom spustiti u rastvor, kako se konstanta

elektrode ne bi promenila (slika 7). Doterati temperaturu termosta-

ta ta~no na 20°C i rastvor termostatirati najmanje 10 minuta pre

merenja.

Medenica / Male{ev

196

DIIT

E S

O ......

Odre|ivanje
specifi~ne i molarne
provodljivosti
jakih elektrolita ( I )

Zadatak eksperimenta

Izmeriti otpore dobijenih rastvora elektrolita i izra~unati speci-

fi~nu i molarnu provodljivost. Grafi~kom metodom i ra~unskim

putem odrediti parametre Kolrau{ove jedna~ine.

Postupak

Prebaciti mre`ni prekida~

power

u polo`aj

(uklju~eno). Pali

se signalna lampica i aparat je spreman za merenje.

Potra`iti preklopnikom za podru~ja,

range

(podru~je), najmanji

otklon kazaljke u smeru strelice na indikator instrumentu. Zatim sa

faktorima multiplikacije podru~ja,

range multiplier

(multiplika-

cija podru~ja), podesiti najmanji mogu}i otklon. Otpor merenog

rastvora elektrolita predstavlja proizvod vrednosti koju pokazuju

preklopnici

range

range multiplier

. Za svaki rastvor merenje

otpora ponoviti po tri puta. Izra~unati srednju vrednost.

Eksperimentalna fizi~ka hemija

197

Slika 6.

Konduktometar

MA 5962

Iskra

– Kranj

1 – glavni prekida~

2 – priklju~ak konduktometrijske }elije

3 – preklopnik podru~ja

4 – faktori multiplikacije

5 – indikator instrument

6 – konduktometrijska }elija

7 – termometar

8 – analizirani rastvor

9 – termostat

Slika 7.

Konduktometrijska }elija

t = .......°C

k = 0,001834 m

–1

Ω

–1

= S (simens)

Eksperimentalna fizi~ka hemija

199

REZULTATI

Tabela 1.

Rezultati merenja

Rastvor

(

Ω

)

(

Ω

)

(

Ω

)

< R > (

Ω

)

(

Ω

–1

) c (mol L

-1

) c (mol m

-3

)

(

Ω

–1

mol

–1

)

– b

√

(

Ω

–1

mol

–1

)

Tabela 2.

Parametri Kolrau{ove jedna~ine

Aparatura i hemikalije

Konduktometar HI8820N

Hanna instruments

(slika 8)

Konduktometrijska }elija

Termostat

Rastvor za kalibraciju

Odre|ivanje temperaturnog koeficijenta provodljivosti

U konduktometrijsku }eliju sipati malo rastvora elektrolita ~ija se

provodljivost odre|uje i isprati je. Isprazniti posudu, sipati rastvor i

staviti posudu u vodeni termostat.

Konduktometrijsku }eliju uroniti u rastvor najvi{e do 1 cm ispod

oznake.

Prebaciti mre`ni prekida~ u polo`aj

Podesiti potenciometar za temperaturni koeficijent na 0% (ne-

ma kompenzacije).

Doterati temperaturu rastvora na 25°C i izmeriti provodljivost

rastvora,

. (Izabrati odgovaraju}i opseg merenja u

S. Ukoliko se

na prikaziva~u pojavi »1«, provodljivost uzorka nalazi se izvan oda-

branog mernog podru~ja.)

Doterati temperaturu rastvora na npr. t = 35°C i izmeriti pro-

vodljivost rastvora

Temperaturni koeficijent

izra~unava se po slede}oj formuli:

Medenica / Male{ev

200

URADITE SAMOSTALNO ...

Odre|ivanje
specifi~ne i molarne
provodljivosti
jakih elektrolita ( II )

Zadatak eksperimenta

Odrediti temperaturski koeficijent provodljivosti rastvora.

Izmeriti specifi~ne provodljivosti dobijenih rastvora elektrolita

i izra~unati molarne provodljivosti.

Grafi~kom metodom i ra~unskim putem odrediti parametre

Kolrau{ove jedna~ine.

100

(

–

)

(t –

) .

(36)

Merenje provodljivosti

a) Postaviti potenciometar za pode{avanje temperaturnog koefici-

jenta na prethodno odre|enu vrednost.

b) Izmeriti vrednosti specifi~ne provodljivosti za dobijene rastvore.

(Vrednost provodljivosti bi}e automatski kompenzovana za vari-

jacije temperature.) Za svaki rastvor ponoviti merenja tri puta.

Izra~unavanje

a) Za date koncentracije elektrolita izra~unati molarne provodlji-

vosti

b) Nacrtati Kolrau{ov grafik i odrediti parametre jedna~ine:

Sa grafika odrediti molarnu provodljivost pri beskona~nom raz-

bla`enju

(odse~ak na ordinati) i konstantu

(nagib prave):

Rezultate prikazati tabelarno i grafi~ki.

Medenica / Male{ev

202

(37)

b = tg

∆Λ

∆√

(39)

– b

√

(38)

t = .......°C

= ..........°C

–1

Eksperimentalna fizi~ka hemija

203

REZULTATI

Tabela 1.

Rezultati merenja

Rastvor

(S m

–1

)

( S m

–1

)

(S m

–1

) <

> (S m

–1

) c (mol L

-1

) c (mol m

-3

)

(S m

mol

–1

)

–

√

(S m

mol

–1

)

Tabela 2.

Parametri Kolrau{ove jedna~ine

Titracija slabe kiseline jakom bazom

(slika 3)

COOH + Na

+ OH

–



O + Na

+ CH

COO

–

U toku titracije, npr. CH

COOH sa NaOH, na samom po~etku

provodljivost je mala zbog slabe disocijacije sir}etne kiseline. Do

Z.T.T. provodljivost postepeno raste jer je proizvod hemijske re-

akcije CH

COONa, ja~i elektrolit od onog po~etnog. Posle Z.T.T.

provodljivost naglo raste usled dodatka jake baze, kada su nosioci

provodljivosti hidroksilni joni. Nagib krive zavisi od koncentracije

titranta i ugao koji zaklapaju grane konduktometrijske krive utoliko

je manji, ukoliko je ve}a koncentracija titranta. Na taj na~in mo`e se

preciznije odrediti Z.T.T. Zakrivljenost krive u blizini Z.T.T poti~e

od hidrolize nastalog natrijum-acetata.

Titracija slabe kiseline slabom bazom

(slika 4)

COOH + NH



O + NH

+ CH

COO

–

Titracijom npr. CH

COOH sa NH

OH, u po~etku titracije, i sve

do Z.T.T, provodljivost raste usled nastajanja soli amonijum-acetata

koja u izvesnoj meri disosuje. Posle Z.T.T. provodljivost se prakti~no

ne menja jer je disocijacija amonijum-hidroksida suzbijena nastalim

amonijum-acetatom. Zakrivljenost krive u blizini Z.T.T. posledica je

hidrolize nastale soli, pa se Z.T.T. odre|uje ekstrapolacijom grana

konduktometrijske krive.

Titracija sme{e jake i slabe kiseline jakom bazom

(slika 5)

Titracijom sme{e, npr. HCl i CH

COOH sa NaOH, nastaje prvo

neutralizacija jake (ta~ka A), a zatim slabe kiseline (ta~ka B). Do ta~-

ke A provodljivost opada zbog smanjenja koncentracije brzih hidro-

gen jona jake kiseline. Posle Z.T.T (A) po~inje disocijacija slabe kise-

line i titracijom nastaje elektrolit natrijum-acetat, koji je ja~i od

same sir}etne kiseline, pa provodljivost blago raste. Posle Z.T.T. i

druge kiseline (B), provodljivost naglo raste i poti~e od prisutnih hi-

droksilnih jona titranta u vi{ku, koji imaju veliku jonsku provod-

ljivost.

Medenica / Male{ev

206

Slika 3.

Titracija slabe kiseline jakom bazom

Slika 4.

Titracija slabe kiseline slabom bazom

Slika 5.

Titracija sme{e jake i slabe kiseline

jakom bazom

+ Cl

–

+ CH

COOH + Na

+ OH

–



O + Na

+ Cl

–

+ CH

COO

–

Mogu}e je titrovati i dve slabe kiseline u sme{i, ali jedino pod

uslovom da im se pKa vrednosti razlikuju najmanje za jednu jedinicu.

Pored reakcija neutralizacije, konduktometrijskom titracijom

mogu se pratiti i

reakcije talo`enja

(

precipitacije

) (slika 6). Pri titraci-

ji, npr. AgNO

sa KCl, deo krive (1) pokazuje neznatnu promenu u

provodljivosti koja nastaje usled zamene srebro jona sa kalijum joni-

ma, a koji imaju malo ve}u jonsku provodljivost.

+ NO

–

+ K

+ Cl

–



AgCl + K

+ NO

–

Posle Z.T.T. provodljivost se znatnije menja zbog prisustva hlorid-

nih jona titranta koji imaju jo{ ve}u jonsku provodljivost. ^e{}e se,

umesto kalijum-hlorida, koristi litijum-hlorid kao titrant, zbog ve}e

razlike u jonskim provodljivostima Li

i Ag

jona.

Kompleksometrijske titracije

mogu se konduktometrijski pratiti

jedino u slu~aju stabilnih kompleksa.

Ovom metodom ne mogu se pratiti oksido-redukcione reakcije,

jer se promenom valentnog stanja jona neznatno menja i njegova

provodljivost.

Konduktometrijska titracija koristi se u onim slu~ajevima kada

se ne mo`e upotrebiti indikator (mutni i obojeni rastvori) ili da bi se

izbegla upotreba indikatora i time otklonila subjektivna gre{ka. Ta-

ko|e se koristi kod titracija veoma razbla`enih rastvora. Jednostav-

nost i osetljivost ove metode omogu}ava njenu primenu u kvantita-

tivnoj analizi mnogobrojnih aktivnih principa u farmaceutskim

preparatima.

U slu~aju da se na mernom instrumentu ure|aja prate promene

otpora rastvora, titraciona kriva ima obrnuti tok od onog kada se

prati provodljivost. Tako }e titraciona kriva u slu~aju titracije jake

kiseline jakom bazom imati izgled kao na slici 7, jer su otpor i pro-

vodljivost obrnuto proporcionalne veli~ine.

Prilikom titracije mora se voditi ra~una o koncentraciji titranta.

Naime, koncentracija titranta mora biti najmanje deset puta ve}a od

koncentracije analiziranog rastvora. Ako to nije slu~aj, javlja se tzv.

efekat razbla`enja

, koji mora dovesti do gre{ke u odre|ivanju Z.T.T.

To se mo`e izbe}i mno`enjem izmerene vrednosti otpora ili provod-

ljivosti sa

faktorom korekcije (f )

Eksperimentalna fizi~ka hemija

207

Slika 6.

Titracija srebro-nitrata

sa kalijum-hloridom

Slika 7.

Titracija jake kiseline jakom bazom

Eksperimentalna fizi~ka hemija

209

DIIT

E S

O ......

Odre|ivanje
koncentracije
natrijum-hidroksida

Zadatak eksperimenta

Izvr{iti dve titracije zadate zapremine natrijum-hidroksida sa

hloridnom kiselinom.

Vrednosti ta~aka za obe titracije ucrtati u isti koordinatni

sistem kao R = f(V). Iz srednje vrednosti zavr{nih ta~aka titracije,

odre|enih grafi~kim putem, odrediti broj grama (m)

natrijum-hidroksida u rastvoru.

Slika 8.

Konduktometar

MA 5961

Iskra

– Kranj

1 – konduktometrijska }elija

2 – analizirani rastvor

3 – magnetna me{alica

4 – preklopnik mernog podru~ja

5 – kru`na skala

6 – indikator instrument – magi~no

oko

Medenica / Male{ev

210

Aparatura i hemikalije

Konduktometar MA 5961

Iskra

– Kranj (slika 8)

Konduktometrijska }elija PP1042

Magnetna me{alica

Natrijum-hidroksid

Hloridna kiselina

Priprema

U ~a{u za titraciju, u kojoj se nalazi magnet, odmeriti odre|enu za-

preminu natrijum-hidroksida i toliku koli~inu destilovane vode da

otvori na konduktometrijskoj }eliji budu ispod nivoa rastvora. Vodi-

ti ra~una da staklena konduktometrijska }elija ne dodiruje magnet.

Uklju~iti magnetnu me{alicu tako da se obezbedi mirno me{anje

rastvora, paze}i da magnet ne o{teti }eliju. U toku titracije odr`avati

brzinu me{alice konstantnom.

Titracija

Uklju~iti aparat u struju i potenciometar sa oznakom

ob~utljivost

(osetljivost) okrenuti udesno do maksimalnog polo`aja. Preklopnik

za biranje mernog podru~ja otpora okretati sve dok se ne na|e po-

dru~je pri kome se magi~no oko otvori. Pre po~etka titracije odredi-

ti ta~nu vrednost otpora rastvora pomo}u kru`ne skale.

Vrednost otpora ~itati pri maksimalnoj {irini tamnog sektora na

magi~nom oku. Ovu vrednost zapisati u tabelu, dodati odre|enu za-

preminu hloridne kiseline iz birete i pro~itati vrednost otpora na ve}

opisani na~in. Ovaj postupak ponavljati sve dok se, posle maksi-

malne vrednosti otpora, ne izmere jo{ najmanje ~etiri vrednosti.

Izvr{iti dve titracije zadate zapremine natrijum-hidroksida. U prvoj

titraciji dodavati hloridnu kiselinu u inkrementima od 0,3 mL, a u

drugoj od 0,2 mL.

Pri o~itavanju voditi ra~una o vrednostima odse~aka na skali pri

prelasku sa jednog na drugo merno podru~je otpora.

Rezultate merenja prikazati tabelarno i grafi~ki.

Aparatura i hemikalije

Konduktometar MA 5962

Iskra

– Kranj (slika 9)

Konduktometrijska }elija

Magnetna me{alica

Sir}etna kiselina

Natrijum-hidroksid

Priprema

U ~a{u za titraciju, u kojoj se nalazi magnet, odmeriti odre|enu za-

preminu sir}etne kiseline i toliku koli~inu destilovane vode da kon-

duktometrijska }elija bude pravilno postavljena. Voditi ra~una da

stakleni deo konduktometrijske }elije ne dodiruje magnet. Uklju~iti

magnetnu me{alicu tako da se obezbedi mirno me{anje rastvora,

paze}i da magnet ne o{teti }eliju. U toku titracije odr`avati brzinu

me{alice konstantnom.

Titracije

a) Prebaciti mre`ni prekida~

power

u polo`aj

. Pali se signalna

lampica i aparat je spreman za merenja.

b) Potra`iti preklopnikom za podru~ja

range

(podru~je) najmanji

otklon kazaljke u smeru strelice na indikator instrumentu. Zatim sa

faktorima multiplikacije,

range multiplier

(multiplikacija pod-

ru~ja), podesiti najmanji mogu}i otklon. Otpor rastvora elektrolita

predstavlja proizvod vrednosti koju pokazuje preklopnik

range

range multiplier

Medenica / Male{ev

212

DIIT

E S

O ......

Odre|ivanje
koncentracije
sir}etne kiseline

Zadatak eksperimenta

Izvr{iti dve titracije zadate zapremine sir}etne kiseline sa

natrijum-hidroksidom.

Vrednosti ta~aka za obe titracije ucrtati u isti koordinatni

sistem kao R = f(V). Iz srednje vrednosti zavr{nih ta~aka titracije,

odre|enih grafi~kim putem, odrediti koncentraciju sir}etne

kiseline.

c) Posle svakog dodatka titranta odrediti vrednost otpora rastvora.

Izvr{iti dve titracije zadate zapremine sir}etne kiseline.

Rezultate merenja prikazati tabelarno i grafi~ki.

Eksperimentalna fizi~ka hemija

213

Slika 9.

Konduktometar

MA 5962

Iskra

– Kranj

1 – konduktometrijska }elija

2 – analizirani rastvor

3 – magnetna me{alica

4 – mre`ni prekida~

5 – preklopnik podru~ja

6 – faktori multiplikacije

7 – indikator instrument

8 – priklju~ak konduktometrijske }elije

(9)

Brzina hemijskih

reakcija

RED REAKCIJA

Odre|ivanje konstante brzine

hidrolize saharoze

Eksperimentalna fizi~ka hemija

217

U hemiji su definisane dve vrste reakcija, kona~ne i povratne ili rav-

note`ne. Kod kona~nih reakcija je, primenom najosetljivijih anali-

ti~kih metoda, mogu}e samo konstatovati prisustvo reaktanata. Na-

protiv, kod ravnote`nih reakcija mogu se odrediti koncentracije i

reaktanata i proizvoda reakcije, koje imaju konstantne vrednosti na

odre|enoj temperaturi.

Hemijska kinetika se bavi ispitivanjem brzine kona~nih i rav-

note`nih reakcija, a ovde }e biti razmatrane brzine kojim se odigra-

vaju kona~ne reakcije. Neke reakcije se odigravaju trenutno, u roku

od milionitog dela sekunde, a neke mogu trajati hiljadama godina.

Iz vremena trajanja reakcije odre|uje se brzina reakcije, odnosno

koli~ina supstancije koja izreaguje ili nastane u jedinici vremena, a

sti~u se i saznanja o mehanizmu reakcije. U farmaciji se hemijska

kinetika primenjuje u biofarmaceutskim i farmakokineti~kim ispiti-

vanjima lekova, kao i za prou~avanje stabilnosti farmaceutskih

preparata, koja zavisi od brzine razlaganja aktivnih supstancija.

Brzina hemijske reakcije defini{e se kao promena koncentracije

supstancije, koja reaguje ili nastaje, u jedinici vremena:

Koncentracija reaktanata se smanjuje u toku reakcije, a koncentraci-

ja proizvoda raste, pa brzina promene koncentracije reaktanata ima

negativan, a brzina nastajanja proizvoda reakcije pozitivan predznak.

Prema tome, brzina reakcije tipa:

A + B

C + D

mo`e se predstaviti na jedan od ~etiri mogu}a na~ina:

Brzina hemijske reakcije zavisi od koncentracije supstancije, pri-

rode supstancije i temperature na kojoj se reakcija odigrava.

RED REAKCIJA

Teorijski princip

v =

(1)

v = –

= –

(2)

Da bi se ova reakcija odigrala, potrebno je da se sudare dva mole-

kula koji imaju odgovaraju}e energije aktivacije, a to je energija koju

molekul mora imati da bi mogao hemijski da reaguje. Prema jedna-

~ini (2), brzina bimolekulske reakcije mogla bi se prikazati na sle-

de}i na~in:

gde je

konstanta brzine bimolekulske reakcije.

Izraz za konstantu brzine

mo`e se izvesti ako su po~etne kon-

centracije reaktanata A i B jednake. Posle vremena

bi}e i c

= c

, pa

se jedna~ina (7) mo`e napisati na slede}i na~in:

Preure|enjem i integraljenjem jedna~ine (8) dobija se:

a re{enjem jedna~ine (9):

Odatle je:

trimolekulskim reakcijama

mora do}i do istovremenog sudara

tri molekula. Verovatno}a odigravanja trimolekulskih reakcija je

veoma mala, pa se takve reakcije naj~e{}e de{avaju u vi{e stupnjeva u

kojima u~estvuju najvi{e dva molekula.

Polimolekulske reakcije

odigravaju se u vi{e stupnjeva, jer vero-

vatno}a da }e se istovremeno sudariti ~etiri, pet ili vi{e molekula je

prakti~no jednaka nuli. Brzinu polimolekulskih reakcija odre|uje

najsporija reakcija, koja mo`e biti mono-, bi- ili trimolekulska.

Eksperimentalna fizi~ka hemija

219

v = –

= k

. c

(7)

–

= k

. c

(8)

(9)

∫

–

∫

t = 0

(10)












–

= k

. t

–

(11)









–

Medenica / Male{ev

220

Koncentracija reaktanta A stepenovana je jedinicom u jedna~ini

za brzinu monomolekulskih reakcija (3), dvojkom u jedna~ini za br-

zinu bimolekulskih reakcija (8) i trojkom u jedna~ini za brzinu tri-

molekulskih reakcija, pa op{ti izraz za brzinu hemijske reakcije ima

slede}i oblik:

Eksponent

naziva se

red reakcije

, a

– brzina reakcije n-tog reda.

Monomolekularnost i red reakcije se poklapaju, pod uslovom da

je reakcija jednostavna, odnosno da se odigrava bez sekundarnih

efekata, kao {to su nastajanje intermedijarnih proizvoda, reverzibil-

nih ili bo~nih reakcija. Me|utim, kod slo`enih reakcija, mono-, bi-,

tri- i polimolekulskih, koje se de{avaju u vi{e stupnjeva, brzina reak-

cije je odre|ena najsporijim procesom, pa se molekularnost i red

reakcije mogu razlikovati. Na primer, petomolekulska reakcija dobi-

janja joda iz vodonik-peroksida i jodidne kiseline, odigrava se u dva

stupnja. Prvi, sporiji proces predstavlja reakciju drugog reda (n = 2),

{to zna~i da ova petomolekulska reakcija ima brzinu drugog reda.

Prema tome, molekularnost se defini{e kao broj molekula reaktana-

ta koji u~estvuju u reakciji, a red reakcije kao zbir eksponenata (n

+ ..... + n

= n) u jedna~ini za brzinu hemijske reakcije (12).

Postoji vi{e metoda za odre|ivanje reda reakcije. Ako se za

dobije ceo broj, zna~i da takva reakcija sadr`i bar dve intermedijar-

ne, najsporije reakcije sli~nih konstanti brzina.

Postoji poseban tip bimolekulskih reakcija, za koje va`i jedna~ina

za brzinu reakcije prvog reda. Po{to se jedan od reaktanata nalazi u

velikom vi{ku, njegova koncentracija ostaje prakti~no nepromenje-

na po zavr{etku reakcije, pa se mo`e smatrati konstantnom. Brzine

ovakvih bimolekulskih reakcija ne razlikuju se od brzine reakcija pr-

vog reda, zbog ~ega se takve reakcije nazivaju

reakcije pseudo-prvog

reda

. Primer ovakve reakcije je hidroliza disaharida (npr. saharoze)

u prisustvu hidrogen jona kao katalizatora, pri ~emu nastaju mono-

saharidi glukoza i fruktoza:

v = –

= k

. c

(12)

+ H

+ C

saharoza

glukoza fruktoza



Medenica / Male{ev

222

Zamenom ovih vrednosti u jedna~inu (6) sledi:

odnosno:

Konstanta brzine reakcije pseudo-prvog reda (

) mo`e se odrediti

kao nagib prave, odnosno koeficijent pravca prikazane linearne loga-

ritamske funkcije.

k =

log

2,303

–

∞

–

∞

(15)

2,303 log

(

–

∞

)

= 2,303 log

(

–

∞

) – k . t

(16)

Eksperimentalna fizi~ka hemija

223

DIIT

E S

O ......

Odre|ivanje
konstante brzine
hidrolize saharoze

Zadatak eksperimenta

Pripremiti rastvor saharoze sa hloridnom kiselinom i meriti

promenu ugla skretanja ravni polarizovane svetlosti.

Izra~unati konstantu brzine hidrolize saharoze.

Grafi~ki prikazati funkciju: log (

–

∞

) = f(t) i odrediti

konstantu brzine hidrolize saharoze kao nagib prave.

Aparatura i hemikalije

Polarimetar (slika 11, strana 69)

Hronometar

Saharoza

Hloridna kiselina

Postupak

Pripremiti 100 mL 20%-tnog rastvora saharoze. Rastvor profiltrirati

da bude potpuno bistar. Izmeriti ugao skretanja ovog rastvora (

Ugao

iznosi polovinu ugla

, jer se za dalji postupak rastvor sa-

haroze razbla`uje u odnosu 1:1 sa hloridnom kiselinom.

Odmeriti 25 mL rastvora saharoze, dodati 25 mL 6 mol L

–1

rast-

vora hloridne kiseline i odmah uklju~iti hronometar, po{to reakcija

po~inje da te~e. Napuniti polarimetarsku cev ovim rastvorom i me-

riti promenu ugla skretanja ravni polarizovane svetlosti. Ostatak rast-

vora zagrevati oko pola sata na 50°C da bi, ubrzanjem reakcije, do{lo

do potpune hidrolize. Zatim rastvor ohladiti i izmeriti ugao

∞

Grafi~ki prikazati funkciju: log (

–

∞

) i odrediti konstantu br-

zine hidrolize saharoze kao nagib prave.

Izra~unati vrednost konstante brzine hemijske reakcije hidrolize

saharoze pod kataliti~kim dejstvom hloridne kiseline. Ako se izra~u-

nate vrednosti za konstantu brzine reakcije sla`u, obra~unate za ra-

zli~ite vremenske intervale, to je dokaz da se radi o brzini monomo-

lekulske reakcije.

Rezultate prikazati tabelarno i grafi~ki.

(10)

Procesi

na granici faza

ADSORPCIJA

Gibzova adsorpciona izoterma

Frojndlihova adsorpciona izoterma

227

Eksperimentalna fizi~ka hemija

Na grani~nim povr{inama ~vrste i te~ne faze postoje nekompenzo-

vane molekulske, atomske ili jonske sile privla~enja.

U unutra{njosti te~ne faze molekul je sa svih strana okru`en dru-

gim molekulima, pa je rezultanta privla~nih sila, koje deluju na taj

molekul, jednaka nuli. Me|utim, kod molekula na povr{ini te~nosti

rezultanta privla~nih sila usmerena je ka unutra{njosti te~nosti, jer

je broj molekula u jedinici zapremine u te~noj fazi ve}i nego u gas-

noj. Posledica postojanja asimetri~nih sila privla~enja je te`nja te~-

nosti da zauzme {to manju povr{inu, koja se zbog toga naziva

povr{inski napon

. To je razlog {to kapi te~nosti imaju sferni oblik,

jer u tom slu~aju telo date zapremine zauzima najmanju povr{inu.

Rastvorena supstancija mo`e smanjiti ili pove}ati povr{inski na-

pon rastvara~a, {to zavisi od interakcije izme|u molekula rastvara~a

i molekula ili jona rastvorka. Kad su privla~ne sile izme|u molekula

rastvorka manje od privla~nih sila izme|u molekula rastvara~a, {to

zna~i da rastvorak ima manji povr{inski napon od rastvara~a, mole-

kuli rastvorka }e se ugra|ivati u grani~ni sloj i smanjivati povr{inski

napon rastvara~a. Po{to je unutra{nji pritisak rastvara~a ve}i od po-

vr{inskog, koncentracija rastvorka bi}e ve}a u grani~nom sloju nego

u unutra{njosti rastvara~a, jer svaki sistem te`i ravnote`nom stanju,

u kome posti`e minimum energije. U suprotnom, kad su me|umo-

lekulske privla~ne sile rastvorka ve}e, povr{inski napon rastvara~a je

manji, a koncentracija rastvorka ve}a u unutra{njosti rastvara~a.

Pojava razli~ite koncentracije rastvorka u grani~nom sloju i u

unutra{njosti rastvora naziva se

adsorpcija

. Prema tome da li je

koncentracija rastvorka u povr{inskom sloju pove}ana ili smanjena,

razlikuju se pozitivna i negativna adsorpcija. Supstancije koje sma-

njuju povr{inski napon rastvara~a i nagomilavaju se na povr{ini

zovu se

povr{inski

ili

kapilarno aktivne

, a one koje pove}avaju po-

vr{inski napon rastvara~a i ~ija je koncentracija u povr{inskom sloju

manja, nazivaju se

povr{inski inaktivne

. Supstancija koja ima oso-

binu da adsorbuje na svojoj povr{ini zove se

adsorbens

, a adsorbo-

vana supstancija

adsorbat

Adsorpcija zavisi od fizi~kih i hemijskih osobina adsorbensa i

adsorbata, spolja{njeg pritiska i temperature. Pri ovim uslovima,

koli~ina adsorbovane supstancije proporcionalna je povr{ini adsor-

bensa i koncentraciji adsorbata.

ADSORPCIJA

(latinski

adsorptio

– zgu{njavanje)

Teorijski princip

Ispitivanja pokazuju da koli~ina adsorbovanog gasa na ~vrstoj

povr{ini raste sa smanjenjem temperature sistema. Na osnovu Le

[atelije-Braunovog (Le Chatelier-Braun) principa mo`e se zaklju~iti

da je adsorpcija gasova egzoterman proces. Adsorpcija te~nih rast-

vora na ~vrstom adsorbensu mo`e biti egzoterman ili endoterman

proces. Pri adsorpciji gasova na ~vrstim povr{inama razlikuju se

fizi~ka

hemijska adsorpcija

(

hemisorpcija

). Fizi~ka adsorpcija se

zasniva na Van der Valsovim (van der Waals) silama, pa se usled toga

mo`e stvoriti vi{emolekulski sloj adsorbata na povr{ini adsorbensa.

Kod hemisorpcije dolazi do stvaranja hemijskih veza, zbog ~ega se

na povr{ini adsorbensa obrazuje monomolekulski sloj adsorbata. U

mnogim slu~ajevima adsorpcija je delimi~no i fizi~ka i hemijska. Ta-

kav primer je adsorpcija kiseonika na aktivnom uglju. Od ukupne

koli~ine adsorbovanog kiseonika, samo onaj deo koji je vezan fizi~-

kim silama mo`e se desorbovati pomo}u vakuuma. Preostali deo je

hemijski vezan kao ugljen-monoksid i ugljen-dioksid i mo`e se sa-

mo delimi~no desorbovati.

Zavisnost adsorbovane koli~ine gasa od pritiska gasa data je

Frojndlihovom

(Freundlich)

adsorpcionom izotermom

gde je:

x – koli~ina adsorbovanog gasa u molovima

m – masa adsorbensa

P – ravnote`ni pritisak gasa

K, n – karakteristi~ne konstante koje zavise od sistema adsor-

bens/adsorbat i temperature.

Jedna~ina (2) mo`e se primeniti i na adsorpciju supstancije iz vr-

lo razbla`enih rastvora, s tim {to se pritisak zamenjuje ravnote`nom

koncentracijom adsorbuju}e supstancije. Na dijagramu (slika 2) vi-

di se da adsorbovana koli~ina gasa u po~etku, pri malim pritiscima,

brzo raste, a zatim se polako pribli`ava nekoj grani~noj maksimal-

noj vrednosti, {to se obja{njava time da je povr{ina adsorbensa za-

si}ena molekulima gasa.

Eksperimentalna fizi~ka hemija

229

= K . P

(2)

Slika 2.

Frojndlihova adsorpciona izoterma

Medenica / Male{ev

230

Logaritmovanjem jedna~ine (2) dobija se izraz:

koji predstavlja pravu prikazanu dijagramom (slika 3). Iz odse~ka

prave na ordinati (log K) izra~unava se konstanta

, a iz nagiba

(1/n) konstanta

log

= log

K +

log

(3)

Slika 3.

Logaritamski oblik

Frojndlihove adsorpcione izoterme

Medenica / Male{ev

232

REZULTATI

Tabela 1.

Odre|ivanje broja kapi u stalagmometru

c (mol L

–1

)

F (n)

< n >

A – broj podeoka koje zauzima jedna kap

B – broj podeoka iznad pro{irenja

C – broj podeoka ispod pro{irenja

D – ukupan broj kapi

E – broj kapi u vi{ku zapremine

[

(B + C) / A

]

F – broj kapi u pro{irenom delu stalagmometra (n) (n = D – E)

voda

Eksperimentalna fizi~ka hemija

233

R = 8,314 J K

–1

mol

–1

T = .........K

= ..........N . m

–1

(tablica 3 u Prilogu)

Tabela 2.

Gibzova adsorpciona izoterma

c (mol L

–1

)

(N m

–1

)

∆σ

∆

∆σ

∆

(mol m

–2

)

Eksperimentalna fizi~ka hemija

235

Primer za izra~unavanje x/m

Za titraciju 10 mL pripremljene 0,1 mol L

–1

sir}etne kiseline pre

adsorpcije utro{eno je 10,15 mL 0,1 mol L

–1

rastvora natrijum-hi-

droksida. Koncentracija ove kiseline je:

× V

= c

× V

0,1 mol L

–1

× 10,15 mL = c

× 10 mL

= 0,1015 mol L

–1

Za adsorpciju 100 mL 0,1015 mol L

–1

sir}etne kiseline odmereno

je 1,0250 g aktivnog uglja (m = 1,025×10

-3

kg).

Posle adsorpcije, za titraciju 10 mL sir}etne kiseline, utro{eno je

8,50 mL 0,1 mol L

–1

rastvora natrijum-hidroksida. To zna~i da je

koncentracija sir}etne kiseline posle adsorpcije c = 0,085 mol L

–1

Razlika u koncentracijama sir}etne kiseline pre i posle adsorpcije

iznosi 0,0165 mol L

–1

, {to zna~i da bi adsorbovana koli~ina kiseline

iznosila 0,0165 molova, da je za adsorpciju uzet 1 L kiseline. S obzi-

rom na to da je adsorpcija izvr{ena sa 100 mL kiseline, adsorbovana

koli~ina

iznosi 0,00165 molova.

Odnos

x/m

je:

0,00165 molova : 1,025 g = 1,61 mol kg

–1

a log x/m:

log x/m = 0,207

Rezultate prikazati tabelarno i grafi~ki.

Medenica / Male{ev

236

t = .........°C

Broj probe

Pre adsorpcije

Posle adsorpcije

V NaOH (mL)

kis.

(mol L

–1

)

V NaOH (mL)

kis.

(mol L

–1

)

Tabela 1.

Titracija acetatne kiseline sa 0,1 mol L

–1

NaOH

Tabela 2.

Frojndlihova adsorpciona izoterma

Proba

m (kg)

c (mol L

–1

)

log c

x(mol)

x/m (mol kg

–1

)

log x/m

log x/m = log K + 1/n log c

Tabela 3.

Konstante Frojndlihove adsorpcione izoterme

t = .........°C

REZULTATI

kis.

=.............mL

Hromatografija

je postupak koji omogu}ava razdvajanje, izolovanje,

identifikaciju i odre|ivanje sastojaka sme{e na osnovu procesa koji

se de{avaju na granici dve faze koje se ne me{aju. Jedna faza je sta-

cionarna i mo`e biti porozno ili granulisano ~vrsto telo, te~nost,

tanak sloj te~nosti adsorbovan na ~vrstom telu i jonoizmenjiva~.

Druga faza je mobilna i mo`e biti gas ili te~nost.

Hromatografski proces sastoji se u tome {to se rastvor sme{e u

mobilnoj fazi propu{ta kroz stacionarnu fazu, pri ~emu dolazi do

raspodele komponenata sme{e izme|u mobilne i stacionarne faze.

Ovaj prelazak komponente iz jedne u drugu fazu de{ava}e se sve dok

odnos koncentracija komponente u stacionarnoj (c

) i mobilnoj fazi

) ne dostigne konstantnu vrednost, koja se naziva

koeficijent

raspodele

a izra`en je Nernstovim (Nernst) zakonom raspodele:

Koeficijent raspodele zavisi od osobina faza, afiniteta komponente

prema fazama i temperature.

Razdvajanje supstancija uzrokovano je fizi~kohemijskim proces-

ima kao {to su adsorpcija, razli~ita raspodela (rastvorljivost) sastoja-

ka sme{e izme|u dve te~ne faze i jonska izmena. Prema ovim pro-

cesima hromatografija se deli na:

adsorpcionu,

podeonu (particionu) i

jonoizmenjiva~ku.

Podela hromatografskih metoda mo`e se izvr{iti i na druge na-

~ine koji zavise od postavljenih kriterijuma: agregatnog stanja mo-

bilne i stacionarne faze, na~ina pomeranja faza i tehnike izvo|enja

hromatografije.

Eksperimentalna fizi~ka hemija

239

HROMATOGRAFIJA

(gr~ki

chroma

– boja i

graphein

– pisati)

Teorijski princip

K =

(1)

Zasniva se na procesima adsorpcije rastvorene supstancije na grani-

ci faza ~vrsto/te~no. Kao stacionarna faza koriste se ~vrste supstanci-

je, koje predstavljaju dobar adsorbens za komponente analizirane

sme{e (slika 1). Naj~e{}e se koriste

aluminijum

oksid

silikagel

mag-

nezijum

-s

ilikat

magnezijum

oksid

, a re|e

aktivni ugalj

. Dobrim ad-

sorbensima smatraju se supstancije koje su porozne, {to zna~i da

imaju veliku aktivnu povr{inu. Mehanizam adsorpcije se zasniva na

fizi~kim i hemijskim vezama izme|u adsorbensa i adsorbata, {to je

detaljnije obja{njeno u poglavlju »Procesi na granici faza«.

Punjenje kolone vr{i se tako {to se adsorbens u granulama, koje

moraju biti pribli`no istog pre~nika, oslobodi od sopstvenog praha i

suspenduje u rastvara~u koji se kasnije koristi kao mobilna faza.

Suspenzija se polako sipa u kolonu koja je prethodno do jedne tre-

}ine napunjena istim rastvara~em. Slavina na koloni se delimi~no

otvori tako da rastvara~ isti~e u kapima. Time se adsorbens izdvaja

iz suspenzije i sle`e u koloni.

Prema na~inu razdvajanja komponenti iz sme{e razlikuju se

slede}e metode:

frontalne analize

istiskivanja

eluiranja

Sastoji se u tome da se ispitivana sme{a kontinuirano propu{ta kroz

kolonu. Ako sme{a sadr`i komponente A, B i C sa redosledom koefi-

cijenata raspodele K

> K

, iz kolone prvo izlazi ~ista kompo-

nenta C, jer se najslabije adsorbuje. Zatim izlazi sme{a komponena-

ta B i C i na kraju eluat koji sadr`i komponente A, B i C u istom

odnosu u kome su unete u kolonu. Ovom metodom mo`e se dobiti

samo deo ~iste komponente C, odnosno ona koja se prva izdvaja iz

kolone, pa ova metoda nema ve}i analiti~ki zna~aj.

Izvodi se tako {to se mala koli~ina sme{e, koja sadr`i komponente A,

B i C, nanese na vrh kolone. Zatim se kroz kolonu kontinuirano

propu{ta rastvor komponente D, koja se mnogo ja~e vezuje za ad-

sorbens od komponenata analizirane sme{e. Komponenta D po-

tiskuje komponente sme{e, koje obrazuju zone. Zbog stalnog dejstva

komponente D, komponente sme{e se ne mogu potpuno razdvojiti,

ve} se zone me|usobno dodiruju. Do izlaska iz kolone, sve tri zone

se kre}u istom brzinom, a po{to izme|u njih nema razmaka, metoda

se ne mo`e pouzdano koristiti za razdvajanje u analiti~ke svrhe.

Medenica / Male{ev

240

Adsorpciona
hromatografija
u koloni

Slika 1.

Adsorpciona hromatografija u koloni

Metoda frontalne analize

Metoda istiskivanja

Medenica / Male{ev

242

Zasniva se na raspodeli (razli~itoj rastvorljivosti) supstancija izme-

|u dve te~ne faze koje se me|usobno ne me{aju. Jedna te~nost je sta-

cionarna faza vezana za ~vrst nosa~, a druga je mobilna faza. Pored

procesa koji se zasniva na razli~itoj rastvorljivosti, de{ava se delimi~-

no i proces adsorpcije na ~vrstom nosa~u. Deli se na:

podeonu hromatografiju u koloni i

podeonu hromatografiju na hartiji i na tankom sloju.

Koeficijent raspodele u podeonoj hromatografiji naziva se

pode-

oni koeficijent

. Karakteristi~an je za sistem u kome postoji kon-

centraciona ravnote`a nekog jedinjenja izme|u dva odre|ena rast-

vara~a, pri konstantnim vrednostima pritiska i temperature.

Kolona se priprema na sli~an na~in kao kod adsorpcione hroma-

tografije, s tim {to je vezana stacionarna faza naj~e{}e voda, a mobil-

na su organski rastvara~i koji se ne me{aju sa vodom.

Za kvalitativnu i kvantitativnu analizu sme{e, kao i u adsorpcio-

noj hromatografiji, uglavnom se koristi metoda eluiranja. Na pri-

mer, sme{a aminokiselina mo`e se analizirati u koloni sa silikagelom

koji je nosa~ stacionarne faze – vode, a mobilnu fazu ~ini neki or-

ganski rastvara~.

Naziva se i hromatografija u »otvorenoj koloni«. Razdvajanje kom-

ponenata vr{i se na hartiji ili plo~ici preko koje je nanet tanak sloj

~vrstog adsorbensa. Protok mobilne faze kroz hartiju ili tanak sloj

ostvaruje se kapilarnim prodiranjem kroz poroznu sredinu. Brzine

kretanja tzv.

zona

ili

mrlja

, od kojih svaka predstavlja jednu izdvo-

jenu komponentu, veoma su va`ne za hromatografski proces, jer od

njih zavisi razdvajanje komponenata. Brzina mobilne faze zavisi, pre

svega, od veli~ine pora u hartiji, odnosno pre~nika ~estica ~vrstog

adsorbensa.

Pri horizontalnom protoku rastvara~a (mobilne faze), tj. kada na

molekule rastvara~a deluju samo kapilarne sile, a ne i sila gravitacije,

front rastvara~a pre}i }e rastojanje

gde je:

k – konstanta koja zavisi od prirode sistema (povr{inski napon i vis

koznost) i temperature

t – vreme za koje rastvara~ pre|e put

Podeona (particiona)
hromatografija

Podeona hromatografija

u koloni

Podeona hromatografija

na hartiji i na tankom sloju

z = (k . t)

1/2

(2)

Eksperimentalna fizi~ka hemija

243

Kod uzlazne ili silazne tehnike razdvajanja, gravitaciona sila sma-

njuje, odnosno pove}ava brzinu kretanja rastvara~a, pa tako uti~e i

na pre|eni put fronta

. Da bi se dobilo dobro razdvajanje, potrebno

je uskladiti vrstu tehnike, vrstu hartije ili tankog sloja, sastav mo-

bilne faze, du`inu trake od hartije, du`inu plo~ice sa tankim slojem i

drugo.

Va`na veli~ina u podeonoj hromatografiji je

vrednost

(reten-

cioni faktor ili faktor zadr`avanja), koja je karakteristi~na za svaku

komponentu u definisanom hromatografskom sistemu i slu`i za

identifikaciju komponente u analiziranoj sme{i. Defini{e se kao od-

nos pre|enog puta komponente (a) i pre|enog puta rastvara~a (b):

Merenje puteva vr{i se od sredi{ta zone nanetog uzorka (anal-

izirane sme{e), koje se zove startna linija, do sredi{ta zone kompo-

nente, odnosno do fronta rastvara~a, kao {to je prikazano na slici 3.

Najve}u R

vrednost ima}e komponenta koja se najbolje rastvara

u organskom rastvara~u (mobilnoj fazi), jer se br`e kre}e od kom-

ponente koja se bolje rastvara u stacionarnoj fazi. Smatra se da su

komponente dobro razdvojene ako je

∆

> 0,05.

Izvodi se u staklenoj posudi, odnosno kadi sa poklopcem koji se do-

bro zatvara. Time se atmosfera posude odr`ava zasi}enom parama

rastvara~a, ~ime se spre~ava njegovo isparavanje sa hartije. [irina

zone izdvojene komponente zavisi od {irine po~etne zone uzorka i

koncentracije uzorka. Pomo}u kalibrisane kapilare ili mikropipete

nanese se rastvor uzorka na nekoliko centimetara od kraja trake od

hartije, koja se nalazi u horizontalnom polo`aju. Uzorak se nanosi u

obliku zone, koja ne treba da ima pre~nik ve}i od 5 mm, ili u obliku

{to tanje crte. Ako je koncentracija uzorka velika, uzorak se pre na-

no{enja razbla`i, a ako je mala, uzorak se nanosi vi{e puta na isto

mesto, s tim {to se pre svakog nano{enja, prethodno naneta zona

mora osu{iti na vazduhu ili u struji ne suvi{e toplog vazduha.

Hartija sa nanetom zonom uzorka mo`e se postaviti u sud tako

da rastvara~ kroz hartiju prolazi horizontalno, nadole ili nagore.

Prema tome, razlikuju se:

horizontalna (kru`na),

silazna i

uzlazna tehnika.

(3)

Slika 3.

Odre|ivanje R

vrednosti

S – start

R – front rastvara~a

a, b, c – pre|eni putevi komponenata

A, B i C

d – pre|eni put rastvara~a

A. Podeona hromatografija

na hartiji

Eksperimentalna fizi~ka hemija

245

Dvodimenzionalna tehnika

je poseban vid tehnike i koristi se kod

supstancija sa bliskim Rf vrednostima. Kad se zavr{i razdvajanje si-

laznom tehnikom, traka se osu{i, okrene za 90° i protok rastvara~a,

naj~e{}e nekog drugog, usmeri normalno na pravac kretanja prvog

rastvara~a (slika 7). Na taj na~in razdvajaju se komponente koje se

nisu prvobitno razdvojile. Da bi dvodimenzionalno razdvajanje us-

pelo, potrebno je da prethodni rastvara~ potpuno ispari ili da bude

hemijski inertan u odnosu na drugi rastvara~.

Razvijanje hromatograma

podrazumeva proces razdvajanja kom-

ponenata na hromatografskoj hartiji. Proces je zavr{en kad front

rastvara~a do|e do unapred odre|ene du`ine ili kad pro|e prethod-

no izmereno vreme razdvajanja komponenata. Olovkom se zabele`i

front rastvara~a, a zatim se hartija osu{i na vazduhu ili u struji toplog

vazduha, koja se propu{ta paralelno sa pravcem prostiranja trake.

Odre|ivanje polo`aja zona

podrazumeva primenu hemijskih ili fi-

zi~kih procesa da bi se zone hromatograma u~inile vidljivim. Fluo-

rescentne supstancije otkrivaju se pomo}u UV lampe, a polo`aj zona

radioaktivnih supstancija odre|uje se ure|ajem za merenje radio-

aktivnosti. U drugim slu~ajevima se, za detekciju zona, naj~e{}e ko-

risti hemijska metoda koja se sastoji u tome da se osu{ena traka prska

odgovaraju}im rastvorom koji hemijski reaguje sa zonama, daju}i

obojena jedinjenja.

Slika 7.

Dvodimenzionalna tehnika

Medenica / Male{ev

246

Kvalitativna analiza

komponenata izvodi se odre|ivanjem R

vred-

nosti i njihovim pore|enjem sa tabli~nim. Ovaj na~in nije dovoljno

pouzdan, jer R

vrednost zavisi od vi{e faktora, kao {to su priroda

komponenti, sastav mobilne faze, temperatura, vrsta hartije i dr. Za-

to se pri publikovanju R

vrednosti moraju definisati i uslovi pod

kojima su one odre|ene. Pouzdaniji na~in identifikacije sastoji se u

tome da se ise~e deo hartije sa zonom nepoznate supstancije i izvr{i

ekstrakcija zone pogodnim rastvara~em. Dobijeni rastvor mo`e se

ispitati hemijskim, fizi~kohemijskim metodama ili hromatografski,

pore|enjem sa hromatogramima referentnih supstancija.

Kvantitativna analiza

komponenata mo`e se izvr{iti na dva na~ina:

direktnim odre|ivanjem koli~ine supstancije u zoni ili ekstrakcijom

supstancije iz zone pogodnim rastvara~em. Supstancije se odre|uju

u izdvojenim zonama direktno na hartiji (

in situ

) spektrofotometri-

jskim metodama, uglavnom na osnovu reflektovane svetlosti. Drugi

na~in se odnosi na hemijsko i fizi~kohemijsko odre|ivanje koli~ine

supstancije u rastvoru dobijenog ekstrakta.

Izvodi se istim tehnikama kao i hromatografija na hartiji:

horizon-

talnom

silaznom

uzlaznom

. Aparatura za razvijanje hromatograf-

skih plo~a prikazana je na slici 8.

Da bi se dobila ravnomerna zasi}enost parom u svim delovima

komore, unutra{nji zidovi se obla`u filtar-hartijom natopljenom

rastvara~em, koji slu`i kao mobilna faza.

B. Podeona hromatografija

na tankom sloju

Slika 8.

Komore za razvijanje hromatografskih

plo~a (shematski prikaz)

(a – silazna; b – uzlazna; c – horizon-

talna tehnika)

Kvalitativna analiza

razdvojenih komponenti, odnosno identi-

fikacija, mo`e se izvr{iti odre|ivanjem R

vrednosti, ali je ova meto-

da jo{ manje pouzdana od one kod hromatografije na hartiji. Uzrok

le`i u dodatnim faktorima koji uti~u na kretanje zona, kao {to su

priroda, aktivnost i debljina sloja adsorbensa, kao i zasi}enost at-

mosfere komore parama rastvara~a. Ako se supstancija ne mo`e sa

sigurno{}u identifikovati pomo}u R

vrednosti ili bojenim reakcija-

ma, sloj adsorbensa sa zonom supstancije pa`ljivo se skine sa plo~e,

zona se ekstrahuje pogodnim rastvara~em i odre|uje nekom od

fizi~kohemijskih metoda.

Kvantitativna analiza

se mo`e vr{iti direktno na plo~i spektrofo-

tometrijskim metodama, uglavnom na osnovu merenja intenziteta

reflektovane svetlosti, pod uslovom da su zone obojene, da fluoresci-

raju ili reaguju sa pogodnim reagensom, daju}i obojeno jedinjenje.

Ako se zona skida zajedno sa slojem adsorbensa, onda se analiza vr{i

nekom klasi~nom kvantitativnom metodom.

Hromatografija na hartiji i na tankom sloju ima veliku primenu

u istra`iva~kim i rutinskim odre|ivanjima. Sa razvojem hromato-

grafije na tankom sloju, kao i gasne, odnosno te~ne hromatografije,

smanjena je primena hromatografije na hartiji. Tankoslojna hro-

matografija na{la je {iroku primenu u farmaciji. U ispitivanju i kon-

troli lekova primenjuje se kako u analizi polaznih sirovina, tako i

me|uproizvoda i finalnih proizvoda. Tako|e se koristi i u pra}enju

stabilnosti lekova, zatim za odvajanje i odre|ivanje aktivnih princi-

pa lekova i njihovih degradacionih proizvoda. Ova metoda se mo`e

primeniti i na lek i na biolo{ki materijal. U biohemijskim i farmako-

lo{kim ispitivanjima primenjuje se za odre|ivanje metabolita lekova

u telesnim te~nostima. U analizi `ivotnih namirnica koristi se za

odre|ivanje npr. ostataka pesticida, za odvajanje i identifikaciju

aminokiselina ili za odre|ivanje boja koje se koriste kao aditivi. U

toksikolo{kim analizama koristi se za odre|ivanje npr. insekticida u

razli~itim materijalima.

Ovde su pomenuti samo neki karakteristi~ni primeri primene

tankoslojne hromatografije u farmaciji.

Medenica / Male{ev

248

Zasniva se na razlikama u afinitetu jonskih vrsta u rastvoru prema

izmeni sa jonima aktivnih grupa koje poseduju neki adsorbensi.

Takvi adsorbensi mogu biti neorganskog i organskog porekla, sin-

teti~ki i prirodni. Prema tome da li u aktivnim grupama sadr`e mo-

bilne katjone ili anjone, dele se na

katjonske

anjonske izmenji-

va~e

. Primena jonskih izmenjiva~a u analiti~ke svrhe je razli~ita:

razdvajanje elemenata sli~nog hemijskog pona{anja (npr. lantanida i

aktinida), odvajanje jonskih od nejonskih vrsta, razdvajanje jona,

razdvajanje katjona od anjona, koncentrisanje jona metala iz vrlo

razbla`enih rastvora i odre|ivanje koncentracije.

U praksi se, uglavnom, koriste visokopolimerne smole koje sa-

dr`e aktivne kiselinske ili bazne grupe, ~iji se joni izmenjuju sa joni-

ma iz rastvora. Katjonski izmenjiva~i sadr`e kiselinske grupe, kao

{to su –SO

H i –COOH, a anjonski izmenjiva~i sadr`e bazne grupe,

kao {to su –OH ili amino grupe –NH

, –NHR i –NR

. Mehanizam

izmene katjona izme|u katjonskog izmenjiva~a i analiziranog rast-

vora, npr. NaCl, zasniva se na ravnote`noj reakciji:

R–SO

H + NaCl



R–SO

Na + HCl

a mehanizam izmene anjona izme|u anjonskog izmenjiva~a i rast-

vora NaCl:

R–OH + NaCl



R–Cl + NaOH

Jonoizmenjiva~ka hromatografija se naj~e{}e izvodi u koloni, ko-

ja se mo`e puniti raznim vrstama organskih katjonskih i anjonskih

izmenjiva~kih smola (slika 9). Suspenzija izmenjiva~a u vodi sipa se

u kolonu koja je delimi~no napunjena vodom, pri ~emu treba paziti

da u kolonu ne u|e vazduh. Na kraju se ispusti vi{ak vode, ali tako

da iznad smole uvek mora postojati sloj te~nosti, bez obzira da li je

kolona u pripremi ili je u toku jonska izmena.

Pri prvom kori{}enju izmenjiva~i nisu dovoljno ~isti za anali-

ti~ke svrhe, pa ih je potrebno

pre~istiti

. Katjonski izmenjiva~i se vi{e

puta naizmeni~no ispiraju sa: 2 mol L

–1

HCl, destilovanom vodom,

2 mol L

–1

NaCl i ponovo destilovanom vodom. Ako je potreban iz-

menjiva~ u H–obliku, poslednje ispiranje se vr{i kiselinom, a kad se

`eli Na–oblik, poslednji se propu{ta NaCl. Na kraju se izmenjiva~

ispira destilovanom vodom do negativne reakcije na odgovaraju}i

jon (H

ili Na

). Anjonski izmenjiva~i se naizmeni~no ispiraju sa:

2 mol L

–1

NaCl, destilovanom vodom, 2 mol L

–1

NaOH i ponovo

Eksperimentalna fizi~ka hemija

249

Jonoizmenjiva~ka
hromatografija

Slika 9.

Kolona sa smolom

Razdvajanje jona u koloni vr{i se na osnovu afiniteta odre|enih

jona prema smoli. Afinitet zavisi od vi{e faktora. U vodenim rastvo-

rima afinitet prema smoli raste sa pove}anjem naelektrisanja jona.

Ako razli~ite jonske vrste imaju jednaka naelektrisanja, ve}i afinitet

prema smoli ima jon manjeg radijusa.

Kvalitativna analiza se naj~e{}e vr{i metodom eluiranja. Ako se

na vrh kolone sa anjonskom smolom sipa odre|ena zapremina anali-

zirane sme{e kiselina, a zatim vr{i eluiranje vodom, u gornjem delu

kolone do}i }e do izmene anjona smole sa anjonom ja~e kiseline,

prema kojoj smola ima najve}i afinitet. Zatim }e se izmeniti slabija

kiselina, pa ostale. Na ovaj na~in posti`e se razdvajanje kiselina u an-

jonskim i baza u katjonskim izmenjiva~ima, ~ija razlika u pK vred-

nostima mo`e biti manja od 0,05 jedinica.

Kvantitativna analiza

se vr{i tako {to se odre|ena zapremina

analiziranog rastvora sipa na vrh kolone, a zatim vr{i sporo eluiranje

vodom da bi se izvr{ila kvantitativna izmena jona. Ako se u katjon-

skom izmenjiva~u odre|uje koncentracija rastvora NaCl, u eluatu }e

se, prema prikazanoj reakciji izmene katjona, na}i ekvivalentna koli-

~ina HCl. Eluiranje vodom vr{i se do neutralne reakcije, {to se pro-

verava lakmus-trakom. Eluat sa HCl, sakupljen u erlenmajeru, titruje

se rastvorom NaOH poznate koncentracije uz metiloran` kao indi-

katorom. Iz utro{ene zapremine NaOH i poznate zapremine anali-

ziranog NaCl, izra~unava se koncentracija NaCl, prema izrazu:

gde je:

M – koncentracija u mol L

–1

V – zapremina rastvora.

U slu~aju da se rastvor NaCl propu{ta kroz anjonski izmenjiva~,

u eluatu }e biti NaOH, a kao titrant koristi}e se rastvor HCl poznate

koncentracije.

Upotrebljene smole mogu se

regenerisati

i vi{e stotina puta, a da

ne do|e do smanjenja kapaciteta. Regenerisanje katjonskih smola

vr{i se sa 2 mol L

–1

hloridnom kiselinom, a anjonskih sa 2 mol L

–1

natrijum-hidroksidom, da bi se aktivne grupe ponovo zasitile aktiv-

nim jonima. Eluiranje pomo}u kiseline, odnosno baze izvodi se vi{e

puta, a zatim se ispira destilovanom vodom do neutralne reakcije.

Eksperimentalna fizi~ka hemija

251

NaCl

NaOH

NaCl

(5)

Jedna od najva`nijih primena smola za izmenu jona je pre~i{}a-

vanje vode tzv. »hladnim postupkom« bez destilacije. Tako se dobija

dejonizovana voda koja je ~esto boljeg kvaliteta nego ona dobijena

klasi~nom destilacijom. Postupak se sastoji u propu{tanju vode prvo

kroz jak katjonski, zatim kroz jak anjonski izmenjiva~ i na kraju kroz

kolonu sa sme{om anjonskog i katjonskog izmenjiva~a. Jonski iz-

menjiva~i se veoma uspe{no koriste i za pre~i{}avanje radioaktivnih

voda.

Pomo}u katjonskih izmenjiva~a razdvajaju se aminokiseline,

masne kiseline, kiseline od baza, koje su rastvorne u vodi. Anjonski

izmenjiva~i se koriste za razdvajanje alkaloida, hlorofenola, hemo-

globina, aldehida, ketona, organskih kiselina male molarne mase i

drugo.

Medenica / Male{ev

252

Pribor i hemikalije

Komora za hromatografiju (slika 8)

Plo~ica sa tankim slojem od silikagela

Sme{a organskih rastvara~a (mobilna faza)

Analizirana sme{a za razdvajanje

Priprema

Komoru za hromatografiju pripremiti kao {to je prikazano na slici 8.

Zidove komore oblo`iti filtar-hartijom natopljenom mobilnom fa-

zom, da bi atmosfera komore bila ravnomerno zasi}ena parama

rastvara~a. U komoru zatim sipati rastvara~ (mobilna faza) tako da

pokrije dno i poklopiti komoru.

Postupak

Na jedan kraj plo~ice sa tankim slojem od silikagela naneti jednu

kap sme{e i centar dobijene mrlje ozna~iti kao start. Plo~icu postavi-

ti u komoru tako da se mrlja nalazi nekoliko milimetara iznad nivoa

rastvara~a. Kada rastvara~ do|e skoro do kraja plo~ice, izvaditi plo-

~icu iz komore i obele`iti front rastvara~a. Na osu{enoj plo~ici obe-

le`iti centre mrlja koje su se razdvojile i izra~unati njihove R

vred-

nosti.

Grafi~ki prikazati dobijeni hromatogram na tankom sloju.

Medenica / Male{ev

254

URADITE SAMOSTALNO...

Podeona
hromatografija na
tankom sloju

Zadatak eksperimenta

Podeonom hromatografijom razdvojiti komponente iz

analizirane sme{e i izra~unati njihove R

vrednosti.

Grafi~ki prikazati dobijeni hromatogram.

Aparatura i hemikalije

Kolona sa katjonskom smolom Dowex-50 (slika 9)

Hloridna kiselina

Natrijum-hlorid

Natrijum-hidroksid

Destilovana voda

Metiloran`

Priprema

a) Punjenje kolone

Kolonu sa smolom pripremiti kao {to je prikazano na slici 9. Dno

kolone zatvoriti sinterovanom plo~icom ili staklenom vunom, a za-

tim napuniti kolonu smolom. Kolona se priprema tako {to se vode-

na suspenzija smole uliva u kolonu, pri ~emu treba voditi ra~una da

u koloni ne ostanu mehuri}i vazduha. Smolu treba prethodno os-

taviti neko vreme da bubri u vodi. Vrh kolone u~vrstiti sa malo stak-

lene vune. Iznad smole uvek mora postojati sloj te~nosti.

b) Regenerisanje smole

Kroz kolonu sa katjonskim izmenjiva~em propustiti rastvor hlorid-

ne kiseline, a zatim ispirati destilovanom vodom do neutralne reak-

cije, koja se proverava lakmus-trakom.

Eksperimentalna fizi~ka hemija

255

URADITE SAMOSTALNO ...

Jonoizmenjiva~ka
hromatografija

Zadatak eksperimenta

Regenerisati smolu.

Odrediti kapacitet smole.

Odrediti koncentraciju rastvora natrijum-hlorida.

Eksperimentalna fizi~ka hemija

257

REZULTATI

Tabela 1.

Odre|ivanje kapaciteta smole (C) i koncentracije (c)

rastvora natrijum-hlorida

smole

(mmol g

–1

)

V NaCl (mL)

c NaOH (mol L

–1

)

V NaOH (mL)

c NaCl (mol L

–1

)

Pojava usmerenog kretanja koloidnih i drugih naelektrisanih ~estica

u polju jednosmernog elektri~nog napona naziva se

elektroforeza

To je elektromigraciona metoda koja spada u grupu osetljivih meto-

da separacije. Koristi se za kvalitativnu i kvantitativnu analizu pravih

(jonoforeza) ili koloidnih rastvora (elektroforeza), ali je usvojen je-

dinstven naziv elektroforeza.

Razdvajanje komponenata iz analizirane sme{e izvodi se na os-

novu razli~itog predznaka naelektrisanja ~estica. Ako ~estice kom-

ponenata imaju isti predznak naelektrisanja, onda se razdvajanje

vr{i na osnovu razli~ite pokretljivosti, koja zavisi od koli~ine naelek-

trisanja i veli~ine ~estica. Jonska pokretljivost ~estica zavisi i od elek-

tri~nog polja izme|u dve elektrode, koje su povezane sa izvorom

jednosmerne struje. Elektri~na sila

, koja izaziva kretanje ~estice,

jednaka je proizvodu koli~ine naelektrisanja ~estice

i ja~ine elek-

tri~nog polja

Ja~ina elektri~nog polja defini{e se kao odnos razlike potencijala

i rastojanja izme|u elektroda.

Na jon ili naelektrisanu koloidnu ~esticu u kretanju deluje i sila

trenja

, koja se suprotstavlja kretanju ~estica. Ona zavisi od vis-

koznosti sredine

, polupre~nika ~estice

i brzine kretanja ~estice

Kad se ~estica na|e u elektri~nom polju, u po~etku se kre}e spo-

ro, a zatim sve br`e, pri ~emu raste

prema jedna~ini (2). Kad se

sile izjedna~e:

~estica se dalje kre}e nekom konstantnom brzinom v, koja se izra~u-

nava iz jedna~ina (1), (2) i (3):

Eksperimentalna fizi~ka hemija

259

ELEKTROFOREZA

Teorijski princip

= Q . E

(1)

. r . v

(2)

= F

(3)

v =

Q . E

. r

(4)

Kao podloga za analiziranu sme{u koristi se filtar-hartija, a u po-

slednje vreme celuloza-acetat, ~ija je struktura homogenija, pa se

dobijaju br`a i bolja razdvajanja. U upotrebi su i druge vrste podlo-

ga, kao {to su agar-gel, silikagel, jonske izmenjiva~ke smole, a poseb-

no gelovi poliakrilamida i amidona zbog njihove velike mo}i razd-

vajanja.

Katodni i anodni prostor ure|aja za elektroforezu ispunjeni su

rastvorom elektrolita, odnosno pufera, ~ija vrednost pH i jonska ja-

~ina zavise od prirode analizirane sme{e. Krajevi trake su uronjeni u

rastvor pufera, koji putem kapilarnog kretanja kvasi celu traku i

omogu}ava protok struje izme|u elektroda.

Razdvajanje sme{e, koja je prethodno naneta na podlogu, izvodi

se pri unapred utvr|enim vrednostima ja~ine struje i napona, kao i

vremena trajanja elektroforeze. Elektroforetsko pomeranje ~estica,

koje zavisi od ovih karakteristika, mo`e se izra~unati ili odrediti ek-

sperimentalnim putem. Po zavr{etku elektroforeze, podloga se su{i,

a razdvojene zone mogu se otkriti posmatranjem pod UV lampom

ili kva{enjem odgovaraju}im reagensima koji daju bojene reakcije.

Koncentracije pojedinih komponenti odre|uju se tako {to se ise~ene

zone rastvore u pogodnom rastvara~u, a dobijeni rastvori odre|uju

fotometrijski.

Eksperimentalna fizi~ka hemija

261

Slika 1.

Ure|aj za elektroforezu

S – izvor naizmeni~ne struje

T – ispravlja~

R – otpornik

A – ampermetar

V – voltmetar

E – kada za elektroforezu

k – katodni prostor

a – anodni prostor

Medenica / Male{ev

262

Elektri~ne osobine koloidnih i drugih ~estica zavise od pH rast-

vora, koji treba tako podesiti da joni postignu maksimalnu pokret-

ljivost. Slabe kiseline disosuju u baznoj sredini, pri ~emu nastaju

molekulski anjoni, dok slabe baze disosuju u kiseloj sredini, daju}i

molekulske katjone. Neki amfoterni makromolekuli, kao {to su be-

lan~evine, poseduju aktivne bo~ne grupe, koje mogu biti pozitivno

ili negativno naelektrisane u zavisnosti od pH rastvora. Pri odre|enoj

pH vrednosti mo`e do}i do izjedna~enja broja pozitivnih i nega-

tivnih naelektrisanja u makromolekulu, tako da je ukupno naelek-

trisanje molekula jednako nuli. Ta pH vrednost naziva se

izoelek-

tri~na ta~ka

, pri kojoj se molekuli ne kre}u u elektri~nom polju, pa

im je pokretljivost jednaka nuli (u = 0).

Jonska ja~ina i jonska sredina rastvora pufera uti~u na ja~inu

elektri~nog polja i pokretljivost analiziranih ~estica. Velika koncen-

tracija jona smanjuje ja~inu elektri~nog polja i pokretljivost ~estica,

pa je elektroforeza produ`ena. Razdvajanje pri jonskoj ja~ini jed-

nakoj nuli nije mogu}e, jer je neophodna izvesna koncentracija elek-

trolita radi odr`avanja elektri~ne provodljivosti rastvora. S druge

strane, odsustvo jona pove}ava mogu}nost koagulacije koloidnih

~estica i talo`enja makromolekula ili njihovo spajanje u aglomerate.

Zbog toga se radi sa puferima, ~ija se jonska ja~ina nalazi u intervalu

0,05 do 0,1 mol L

–1

Jonska sredina podrazumeva odgovaraju}u prirodu rastvara~a i

elektrolita. [to je ve}a polarnost rastvara~a, manja je sila uzajamnog

privla~enja suprotno naelektrisanih ~estica. Zbog toga su elektri~ne

osobine koloidnih i drugih ~estica, ~ije se razdvajanje vr{i, ja~e

izra`ene u vodi, ~ija je elektri~na permitivnost ve}a od etanola i

drugih organskih rastvara~a. [to se ti~e prirode elektrolita oni mogu

obrazovati komplekse sa ~esticama koje se elektroforetski razdvaja-

ju. Na primer, gvo`|e(III)-jon u prisustvu hloridnih jona stvara, u

zavisnosti od pH, komplekse FeCl

, FeCl

i FeCl

–

I vrsta podloge mo`e uticati na elektroforetsko kretanje ~estica.

Neke podloge poseduju na svojoj povr{ini funkcionalne grupe spo-

sobne da adsorbuju naelektrisane ~estice, ostvaruju}i sa njima fizi~-

ke ili hemijske veze. Pojava adsorpcije usporava kretanje ~estica i

izaziva {irenje zona, zbog ~ega mo`e do}i do njihovog preklapanja.

Na elektroforetsko kretanje ~estica uti~e i pojava

elektroosmoze

Posmatranjem rastvora pufera u katodnom i anodnom prostoru,

koji su premo{}eni podlogom natopljenom elektrolitom, mo`e se

zapaziti kretanje te~nosti prema katodi. Ova pojava obja{njava se

~injenicom da se te~nost u kontaktu sa povr{inom ~vrste podloge

Medenica / Male{ev

264

Aparatura i hemikalije

Ure|aj za izvo|enje elektroforeze (slika 1, str 261)

Filtar-hartija Watman M4

Acetatni pufer pH 4,6

Analizirana sme{a Fe(II)– i Fe(III)– jona

Postupak

Ise}i trake filtar-hartije Watman M4 {irine 1,5 cm i du`ine 30 cm. Na

rastojanju od 10 cm sa jedne strane trake obele`iti grafitnom olov-

kom liniju koja ozna~ava start. Nakvasiti traku destilovanom vodom

i polo`iti je na ~istu filtar-hartiju.

U sahatnom staklu pome{ati po 1 mL osnovnih rastvora Fe(II)– i

Fe(III)–jona i dodati 2 mL acetatnog pufera pH 2,5. Izme{ati rastvor

staklenim {tapi}em i kapilarom naneti ispitivanu sme{u u obliku {to

tanje crte du` startne linije.

U sve ~etiri pregrade kade za elektroforezu sipati acetatni pufer

pH 4,6. Postaviti traku na nosa~ tako da ne dodiruje dno kadice i da

bude dovoljno zategnuta. Krajevi trake, kao i grafitne elektrode, mo-

raju biti uronjeni u rastvor acetatnog pufera. Kada je sve postavljeno,

uklju~iti aparat i odgovaraju}im potenciometrom doterati napon

struje na 250 V. Elektroforetsko razdvajanje ove test-sme{e traje 2 sata.

Po zavr{etku razdvajanja isklju~iti aparat i izvaditi nosa~ sa trakama.

Ostaviti trake da se osu{e, a zatim provu}i kroz rastvor kalijum-hek-

sacijanoferata. Dobijaju se dve obojene trake koje treba identifiko-

vati i napisati reakcije identifikacije.

URADITE SAMOSTALNO...

Elektroforetsko

razdvajanje sme{e

(II)– i F

(III)– jona

Zadatak eksperimenta

Elektroforezom na papiru razdvojiti Fe(II)– i Fe(III)– jone

iz sme{e.

Prikazati dobijeni elektroforezogram i napisati reakcije

identifikacije.

Prilog

TABLICE

Gustine i koeficijenti viskoznosti za vodu na razli~itim temperaturama

Atomski i strukturni parahori

Gustine i koeficijenti povr{inskog napona za vodu na razli~itim temperaturama

Krioskopske konstante rastvara~a

Specifi~na toplota vode

Refrakcije atoma i veza na

= 589 nm

Standardni potencijali elektroda

Specifi~na provodljivost 0,0100 mol L

–1

rastvora kalijum-hlorida

Molarna jonska provodljivost

u vodi na 25°C

Molarne mase hemijskih elemenata

Simboli fizi~kih veli~ina

Simboli fizi~kih veli~ina koji se pi{u gr~kim slovima

Gr~ki alfabet

STATISTI^KA OBRADA REZULTATA

t°C

(kg m

-3

)

(N m

-1

)

999,10

0,07348

998,94

0,07334

998,77

0,07320

998,60

0,07305

998,41

0,07289

998,20

0,07275

997,90

0,07260

997,77

0,07244

997,54

0,07228

997,30

0,07212

997,04

0,07196

996,78

0,07180

996,51

0,07164

996,23

0,07147

995,94

0,07131

995,65

0,07115

Rastvara~

K (K kg mol

–1

)

Kamfor

40,00

Ugljen-tetrahlorid

30,00

Fenol

7,27

Naftalen

6,94

Benzen

5,12

Sir}etna kiselina

3,90

Ugljen-disulfid

3,80

Voda

1,86

Medenica / Male{ev

268

Tablica 3.

Gustine i koeficijenti

povr{inskog napona za vodu

na razli~itim temperaturama

Tablica 4.

Krioskopske konstante

rastvara~a

t°C

(KJ kg

–1

)

4,2177

4,1922

4,1858

4,1819

4,1796

4,1785

4,1786

4,1807

4,1844

4,1896

4,1964

4,2051

100

4,2160

Atom/veza

Refrakcija

[

]

2,418

1,100

O (karbonilni)

2,212

O (etarski)

1,643

O (hidroksilni)

1,525

N (prim. amin)

2,322

N (sec. amin)

2,499

N (terc. amin)

2,840

5,967

8,865

13,900

–C=C–

1,733

–C

≡

C–

2,398

Eksperimentalna fizi~ka hemija

269

Tabela.5.

Specifi~na toplota vode

Tablica 6.

Refrakcije atoma i veza

(u CGS jedinicama)

= 589 nm

Eksperimentalna fizi~ka hemija

271

Katjon

(

Ω

–1

mol

–1

)

Anjon

(

Ω

–1

mol

–1

)

127,2

–

78,1

119,0

COO

–

40,9

77,2

–

76,3

105,6

160,0

107,2

ClO

–

67,3

73,5

–

55,4

38,7

–

76,8

349,6

2–

138,6

106,0

–

71,5

73,5

–

199,1

Tablica 9.

Molarna jonska provodljivost

u vodi na 25°C

Medenica / Male{ev

272

Element

Simbol

kg mol

–1

Element

Simbol

kg mol

–1

Aluminijum

0,02698

Kalijum

0,03910

Antimon

0,12175

Kiseonik

0,01600

Arsen

0,07492

Kobalt

0,05893

Azot

0,01400

Magnezijum

0,02430

Bakar

0,06354

Mangan

0,05494

Bizmut

0,20898

Natrijum

0,02299

Brom

0,07990

Nikl

0,05871

Cink

0,06537

Olovo

0,20720

Fluor

0,01899

Paladijum

0,10640

Gvo`|e

0,05585

Platina

0,19509

Hlor

0,03545

Srebro

0,10787

Hrom

0,05199

Sumpor

0,03206

Jod

0,01269

Ugljenik

0,01201

Kadmijum

0,11240

Vodonik

0,00100

Kalcijum

0,04008

@iva

0,20059

Simbol

Fizi~ka veli~ina

SI jedinica

molarna apsorptivnost

mol

–1

aktivnost

povr{ina

apsorbancija

relativna atomska masa

debljina sloja, {irina

masena koncentracija

kg m

-3

molarna koncentracija

mol m

-3

Tablica 10.

Molarne mase hemijskih elemenata

Tablica 11.

Simboli fizi~kih veli~ina

koeficijent raspodele

A,B

koeficijent selektivnosti jon-selektivne elektrode

konstanta protolize

du`ina

masa

molalna koncentracija

mol kg

–1

molarna masa

kg mol

–1

relativna molekularna masa

koli~ina supstancije

mol

indeks prelamanja

broj kapi

broj elektrona

indeks prelamanja staklene prizme

pritisak

Pa = N m

–2

proizvod rastvorljivosti

mol

–6

koli~ina elektriciteta

koli~ina toplote

molarna toplota rastvaranja

J mol

–1

radijus, polupre~nik

gasna konstanta

R = 8,314

J K

–1

mol

–1

elektri~ni otpor

Ω

1,2

molarna refrakcija sme{e

mol

–1

molarna refrakcija

mol

–1

konstanta podeone hromatografije

vreme

Celziusova temperatura

t°C = T – 273,15 K

termodinami~ka temperatura

jonska pokretljivost

–1

napon

brzina

m s

–1

brzina reakcije

mol m

–3

–1

zapremina

gradijent brzine

–1

molski udeo supstancije

broj elektrona

koli~ina naelektrisanja

Medenica / Male{ev

274

IMBOL

IZI

KA VELI

INA

JEDINICA

stepen protolize

podeoni (particioni) koeficijent

opti~ka rotacija

rad

[α]

specifi~na rotacija

rad m

–1

[α]

molarna rotacija

rad m

mol

–1

faktor aktivnosti

Gibzova povr{inska koncentracija

mol m

–2

koeficijent viskoznosti

Pa s

viskoznost rastvara~a

Pa s

specifi~na viskoznost

red

redukovana viskoznost

–1

[η]

unutra{nja viskoznost

–1

fluidnost

–1

m s

specifi~na provodljivost elektrolita

S m

–1

talasna du`ina

–

provodljivost anjona

S m

mol

–1

provodljivost katjona

S m

mol

–1

molarna provodljivost elektrolita

S m

mol

–1

molarna provodljivost pri beskona~nom razbla`enju

S m

mol

–1

specifi~na otpornost

Ω

gustina

kg m

–3

koeficijent povr{inskog napona

N m

–1

stehiometrijska suma

vreme

Eksperimentalna fizi~ka hemija

275

Tablica 12.

Simboli fizi~kih veli~ina koji se pi{u gr~kim slovima

Razlika izme|u preciznosti i ta~nosti prikazana je na slici.

Preciznost

ukazuje na slaganje rezultata dva ili vi{e merenja spro-

vedena pod istim uslovima. Definisana je standardnom devijacijom

, varijansom ili parcijalnom disperzijom

, relativnom standard-

nom devijacijom

RSD

, koeficijentom varijacije

, standardnom de-

vijacijom srednje vrednosti

< x >

i amplitudom variranja

. Preciz-

ni su oni rezultati koji su reproduktivni.

Standardna devijacija (S)

gde je:

– < x >) – odstupanje i-tog merenja od srednje vrednosti < x >

(n – 1) – broj stepeni slobode

n – broj merenja.

Srednja vrednost < x > dobija se kao koli~nik sume svih rezultata

merenja i broja merenja:

Varijansa ili parcijalna disperzija (S

)

Eksperimentalna fizi~ka hemija

277

STATISTI^KA OBRADA REZULTATA

Podrazumeva niz matemati~kih postupaka kojima se tuma~e rezultati merenja

u pogledu njihove

preciznosti

ta~nosti

neta~no i neprecizno

ta~no i neprecizno

neta~no i precizno

ta~no i precizno

S =

i = 1

– <x>)

n –

(1)

i = 1

– <x>)

n –

(3)

<x> =

i = 1

(2)

Relativna standardna devijacija (RSD)

Koeficijent varijacije (K)

Standardna devijacija srednje vrednosti (S

< x >

)

Amplituda variranja

(

) predstavlja razliku izme|u najve}e i

najmanje vrednosti merenja.

Ta~nost

ukazuje na ispravnost merenja. To je mera sigurnosti neke

metode. Smatra se da je ta~an onaj rezultat koji ne odstupa mnogo

od prave vrednosti. Definisana je apsolutnom gre{kom

i relativ-

nom gre{kom

Apsolutna gre{ka (A)

gde je:

– pojedina~na vrednost merenja

x – prava vrednost.

Mo`e imati (+) i (–) predznak, za razliku od matemati~ke apso-

lutne vrednosti.

Kako se apsolutna vrednost ne mo`e odrediti, apsolutna gre{ka

se izra~unava iz srednje vrednosti i tada se naziva

prividna gre{ka

ili

apsolutna gre{ka pojedina~nog merenja

278

RSD =

1000

‰

(4)

K =

100

<x>

(5)

<x>

A = x

– x

√

(6)

(7)

∆

x = x

– <x>

(8)

ROJ MERENJA

POUZDANOST

90%

95%

99%

0,941

0,970

0,994

0,765

0,829

0,926

0,642

0,710

0,821

0,560

0,625

0,740

0,507

0,568

0,680

0,468

0,526

0,634

0,437

0,493

0,598

0,412

0,466

0,568

Medenica / Male{ev

280

Tablica 1.

Kriti~ne vrednosti koli~nika Q

Studentova t raspodela

Za definisanje

granice intervala pouzdanosti

neke metode ko-

risti se

Studentov t test

, koji omogu}ava odre|ivanje verovatnog in-

tervala u kome se nalazi pravi rezultat:

gde je

– ta~nost odre|ivanja, a izra~unava se kao proizvod faktora

Studentove raspodele

i standardne devijacije srednje vrednosti

< x >

Vrednosti faktora Studentove raspodele t, prema broju stepeni

slobode K i pouzdanosti, nalaze se u tablici 2.

<x> ± E

(12)

E = t × S

<x>

(13)

Tablica 2.

Faktori Studentove raspodele

Stepen slobode

Pouzdanost

K = (n – 1)

80%

90%

95%

99%

99,9%

3,08

6,31

12,7

63,7

637

1,89

2,92

4,30

9,92

31,6

1,64

2,35

3,18

5,84

12,9

1,53

2,13

2,78

4,60

8,60

1,48

2,02

2,57

4,03

6,86

1,44

1,94

2,45

3,71

5,96

1,42

1,90

2,36

3,50

5,40

1,40

1,86

2,31

3,36

5,04

1,38

1,83

2,26

3,25

4,78

1,37

1,81

2,23

3,17

4,59

1,36

1,80

2,20

3,11

4,44

1,36

1,78

2,18

3,06

4,32

1,35

1,77

2,16

3,01

4,22

1,34

1,76

2,14

2,98

4,14

Eksperimentalna fizi~ka hemija

281

Primer

Izvr{eno je deset merenja indeksa refrakcije i rezultati su pore|ani

po rastu}em nizu:

= 1,4815

= 1,4830

= 1,4831

= 1,4832

= 1,4833

= 1,4834

= 1,4840

Kona~no, verovatni interval u kome se nalazi pravi rezultat, pre-

ma izrazu (12), iznosi:

< x > ± E = 1,4833 ± 3 ×10

–4

Metoda najmanjih kvadrata

Kalibraciona kriva je, u podru~ju npr. linearne zavisnosti apsorban-

cije od koncentracije rastvora, definisana jedna~inom prave:

y = ax + b

gde je:

a – nagib prave

b – odse~ak na ordinati.

Da bi se ocenila ispravnost eksperimentalno dobijene kalibra-

cione krive, potrebno je konstruisati ovu krivu metodom najmanjih

kvadrata, tzv.

teorijsku krivu

. Za dobijenu pravu parametri

izra~unavaju se iz slede}ih izraza:

gde je:

– koncentracija i-tog rastvora

< x > – srednja vrednost koncentracije

– apsorbancija i-tog rastvora

< y > – srednja vrednost apsorbancije

n – broj merenja.

Eksperimentalna fizi~ka hemija

283

a =

– n <x> . <y>

– n <x>

(14)

b =

<y> – a<x>

(15)

Za izra~unavanje parametara teorijske krive potrebno je

izra~unati vrednosti date u tabeli 1.

Simbol

Vrednost

Simbol

Vrednost

< x >

< y >

< x >

Na osnovu izra~unatih vrednosti parametara

izra~unati teorij-

ske vrednosti apsorbancija (y) za rastvore poznatih koncentracija

(x). Prikazati tabelarno (tabela 2) i na osnovu tabele teorijsku krivu

prikazati grafi~kim putem, a vrednosti dobijene eksperimentalnim

putem uneti samo kao ta~ke. Tako se mo`e videti odstupanje teorij-

skih od eksperimentalnih vrednosti.

Teorijska kriva

a = .........

b = .........

Medenica / Male{ev

284

Tabela 1.

Metoda najmanjih kvadrata

Tabela 2.

1. Atkins P.,

Physical Chemistry

W. H. Freeman and Company,

New York 1990.

2. Atkins P., Clugston M.,

Na~ela fizikalne kemije

[kolska knjiga, Zagreb 1989.

3. Cvita{ T., Kallay N.,

Fizi~ke veli~ine i jedinice

me|unarodnog sustava

Hrvatsko hemijsko dru{tvo, Zagreb

1975.

4. akovi} Lj.,

Koloidna hemija

Tehnolo{ki fakultet, Zavod za izdavanje

ud`benika, Novi Sad 1990.

5. or|evi} S. i saradnici,

Hemijsko tehnolo{ki priru~nik,

Fizi~kohemijske metode

Rad, Beograd 1985.

6. or|evi} S., Dra`i} V.,

Fizi~ka hemija

Tehnolo{ko-metalur{ki fakultet,

Beograd 1990.

7. Egert J., Hok I., [vab G.,

Ud`benik fizi~ke hemije

Nau~na knjiga, Beograd 1966.

8. Ewing G.,

Instrumental Methods of Chemical

Analysis

McGraw-Hill Kogakusha, Ltd., 1975.

9. Filipovi} I., Sabion~elo P.,

Laboratorijski priru~nik

Tehni~ka knjiga, Zagreb 1970.

10. Florence A., Attwood D.,

Physicochemical Principles of Pharmacy

The MacMillan Press Ltd., London

1988.

11. Foti} Lj.,

Instrumentalne metode hemijske

analize

Tehnolo{ko-metalur{ki fakultet,

Beograd 1981.

12. Gleston S.,

Ud`benik fizi~ke hemije

Nau~na knjiga, Beograd 1967.

13. Glasstone S.,

An Introduction to Electrochemistry

D. Van Nostrand Company, inc.,

New York 1954.

14.

Handbook of Chemistry and Physics

forty-third edition,

The Chemical Rubber Publishing Co.,

Cleveland, Ohio 1962.

15. Harrison G., Lord R., Loofbourow J.,

Prakti~na spektroskopija

Nau~na knjiga, Beograd 1962.

16. Ivanovi} D., Vu~i} V.,

Fizika II

Nau~na knjiga, Beograd 1980.

17. Janji} T.,

Teorijski osnovi analiti~ke hemije

Nau~na knjiga, Beograd 1971.

18. Jovanovi} M.,

Elektroanaliti~ka hemija

Tehnolo{ko-metalur{ki fakultet,

Beograd 1978.

19. Macinnes D.,

The Principles of Electrochemistry

Dover Publications, inc., New York

1961.

20. Martin A., Swarbrick J.,

Cammarata A.,

Physical Pharmacy

Lea & Febiger, Philadelphia 1969.

21. Medenica M., Male{ev D.,

Eksperimentalna fizi~ka hemija

i instrumentalne metode

dr Mirjana Medenica, Beograd 1994.

22. Mi{ovi} J., Ast T.,

Instrumentalne metode hemijske

analize

Tehnolo{ko-metalur{ki fakultet,

Beograd 1989.

23. Nikoli} D., Vela{evi} K., Nikoli} K.,

Praktikum instrumentalne analize

Medicinska knjiga, Beograd-Zagreb

1989.

24. Obradovi} M., i saradnici

Hemijsko tehnolo{ki priru~nik, Hemijski

i fizi~ki podaci i veli~ine

Rad, Beograd 1987.

25. Purdy W.,

Methods in Biochemistry

McGraw-Hill Book Company, New

York 1965.

26. Rajkovi} M., Vu~urovi} B.,

Koeficijent selektivnosti jon-selektivne

elektrode

Arhiv za farmaciju, Beograd, 4-5

(1992) 141.

27. Rendle P., Vokins M., Davis P.,

Experimental Chemistry

Edward Arnold Ltd., London 1972.

28. Saunders L.,

Principles of Physical Chemistry

for Biology and Pharmacy

Oxford University Press, London 1971.

29. Skoog A. D.,

Principles of Instrumental Analysis

Saunders College Publishing,

New York 1985.

30. Skoog A. D., West M. D., Holler J. F.,

Fundamentals of Analytical Chemistry

Saunders College Publishing, Fort

Worth 1992.

Eksperimentalna fizi~ka hemija

287

31. Todorovi} M., ur|evi} P.,

Antonijevi} V.,

Opti~ke metode instrumentalne analize

Hemijski fakultet Unuverziteta u

Beogradu, Beograd 1997.

32. [u{i} M.,

Elektrohemija

Nau~na knjiga, Beograd 1970.

33. Vela{evi}-@ivkovi} K., Nikoli} K.,

Osnovi spektroskopskih metoda

Zavod za ud`benike i nastavna

sredstva, Beograd 1986.

34. Veselinovi} S. D.,

Jon-selektivne elektrode

Glasnik Hemijskog dru{tva, Beograd,

43 (1978) 817.

35. Vra~ar Lj. i saradnici,

Eksperimentalna fizi~ka hemija

Tehnolo{ko-metalur{ki fakultet,

Beograd 1990.

Medenica / Male{ev

288

aditivne osobine

adsorbat

227

adsorbens

227, 240, 247

adsorpcija

227

adsorpciona izoterma

Frojndlihova 229

Gibzova 228

alkalna gre{ka

144

Ami}ijeve prizme

53, 54

analizator

63, 67

apsorbancija

77, 78, 88

apsorpcija

apsorpciona mo}

apsorpcioni koeficijent

78, 85

apsorpcioni spektar

87, 94, 101

apsorptivnost

Bekmanov termometar

32, 39

Berov zakon

bimolekulska reakcija

218

boja 75

cevni potenciometar

146

Denijelov spreg

125

Diboskov kolorimetar

79, 81

difrakciona re{etka

disperzija

molarna 51

rotaciona 65

specifi~na 51

Djuarov sud

dodirni napon

dvostruki elektri~ni sloj

126

egzoterman proces

ekscitacija

elektroda

`ivina 133

bakarna 126

cinkana 126

druge vrste 128

fluoridna 152

hinhidronska 137

indikatorska 127

jodna 152

jon-selektivna 151

kadmijumova 133

kalomelova 128

kombinovana 145

merkuro-sulfatna 169

platinska 140, 181

prve vrste 127

pX 151

referentna 127

srebrova 169, 175

srebro-sulfidna 169

staklena 137, 163

standardna vodoni~na 130

vodoni~na 127, 130

zlatna 181

elektroforeza

259

niskonaponska 260

slobodna 260

visokonaponska 260

zonska 260

elektrohemijski ekvivalent

110

elektroliti~ki most

125

elektroliza

109

elektromagnetsko zra~enje

elektromotorna sila

125, 131

elektronski gas

126

elektroosmoza

262

eluat

240

eluent

240, 241

eluiranje

240

endoterman proces

faktor aktivnosti

127

faktor korekcije

207

faradej

109

Faradejev zakon

109

fluiditet

foto}elija

gasna 97

selenska 97

vakuumska 97, 98

fotocev

fotodetektor

96, 97

fotoelektri~ni kolorimetar

fotoelement

fotometar

75, 86, 89

fotometrija

fotomultiplikator

fotostruja

frontalna analiza

240

galvanska }elija

125

grani~ni ugao

52, 54

grani~ni viskozitetni broj

hemisorpcija

229

Heplerov viskozimetar

hidroliza saharoze

221, 223

hiralni centar

hromatografija

239

adsorpciona 240, 253

dvodimenzionalna 245

horizontalna 244, 246

jonoizmenjiva~ka 239, 249, 255

kru`na 244

particiona 239, 242

podeona 239, 242, 254

silazna 244, 246

uzlazna 244, 246

hromatogram

241, 247

hromofore

indeks prelamanja

apsolutni 49

relativni 49

istiskivanje

240

jonska ja~ina

156

kalibracija

kolorimetra 82

pH-metra 148

pH-metra u dve ta~ke 148

pH-metra u jednoj ta~ki 148

stalagmometra 21

viskozimetra 12

kalibraciona kriva

79, 95, 101

kalorimetar

adijabatski 40

sa vodom 40

Eksperimentalna fizi~ka hemija

291

Medenica / Male{ev

292

kalorimetrija

kapacitet smole

250, 256

kapilarna elevacija

kisela gre{ka

144

kiveta

99, 104

koeficijent

apsorpcioni 78, 85

molarni apsorpcioni 78

podeoni 242

povr{inskog napona 15

pravca 154, 157

raspodele 239

selektivnosti jon-selektivne

elektrode 151

viskoznosti 9

koligativne osobine

kolimatorsko so~ivo

86, 95, 99

kolorimetar

kolorimetrija 75

Kolrau{ov zakon

194

komplementarna boja

87, 89

konduktometar

209

konduktometrija

189

konduktometrijska }elija

197

konstanta

brzine hemijske reakcije 218

ebulioskopska 29

kapilarna 15

konduktometrijske }elije 190

krioskopska 29

Kunove jedna~ine 6

protolize 159, 195

stabilnosti kompleksa 159

konstitutivne osobine

krioskopija

kulometar

111, 112

bakrov 111

gasni 112

jodni 112

srebrov 112

kulometrija

pri konstantnoj ja~ini struje 115

pri konstantnom potencijalu 115

kulometrijska titracija

115

neposredna 116

posredna 116

kulon

109

Kun-Mark-Hauvinkova jedna~ina

Lamber-Berov zakon

78, 85, 94

Lamberov zakon

lampa

deuterijumova 96

kvarc-jodna 96

natrijumova 67, 69

vodoni~na 96

volframova 80, 86, 104

Laplasova jedna~ina

Lorenc-Lorencova jedna~ina

lutaju}i elektroni

105

me|ufazni napon

me|upovr{inski napon

16, 20

molarna rotacija

molarni apsorpcioni koeficijent

monohromator

86, 96, 104

monomolekulska reakcija

218

mutarotacija

neredovan zrak

Nernstova jedna~ina

126

Nikolova prizma

Njutnov zakon 3

Omov zakon

189

opacitet

opti~ka aktivnost

opti~ka prizma

opti~ka rotacija

oscilacije

elektri~ne 61, 62

magnetne 61, 62

Ostvaldov viskozimetar

parahor

16, 50

paskal

pH 137

-metar

143, 146

Poazejev zakon

Pogendorfova metoda

131, 175

polarimetar

66, 69, 223

polarimetrija

61, 66, 68

polarizacija

polarizator

63, 67

polarizovana svetlost

62, 65

polaroid

polihromatska svetlost

polimolekulska reakcija

219

potencijal

asimetrije 143

elektrode 126

membranski 143

ravnote`ni 126

standardni 126

potenciometrija

125

potenciometrijska kriva

integralna 160

prvog izvoda 160

drugog izvoda 160

povr{inski napon

15, 231

koeficijent 18

odre|ivanje 17

prehla|enje

proizvod rastvorljivosti

129

provodljivost

189

molarna 192

molarna jonska 193

pri beskona~nom razbla`enju 193

specifi~na 189

pseudo-prvog reda reakcija

220

Raulov zakon

razrez (slit)

99, 104

red reakcije

217, 220

redovan zrak

vrednost

243

refleksiona mo}

refrakcija

atoma 50

molarna 50

sme{e 51

specifi~na 50

veze 50

refraktometar

Abeov 52, 53, 55, 56

imerzioni 52

Pulfrihov 52

refraktometrija

regenerisanje smole

251

reohor

reologija

544(075.8)

543.08(075.8)

MEDENICA, Mirjana

Eksperimentalna fizi~ka hemija / Mirjana

Medenica, Du{an Male{ev ;

[

fotografije

Branislav Nikoli}

] . − [

2. izd.

] . −

Beograd :

M. Medenica, 2002 (Beograd : Akademija) . -

293 str. : ilustr. ; 24 cm

Tira` 1500. - Bibliografija: str.

287-288. - Registar.

ISBN 86-901485-4-X

Male{ev, Du{an

Fizi~ka hemija - Instrumentalni metodi

COBISS-ID 101594124

CIP -

Katalogizacija u publikaciji

Narodna biblioteka Srbije, Beograd

Želiš da pročitaš svih 271 strana?

Prijavi se i preuzmi ceo dokument.

Prijavi se Napravi nalog

Eksperimentalna fizička hemija

Prijava dokumenta

Problemi sa sadržajem

Problemi sa kupovinom i pristupom

Tehnički problemi

Kršenje pravila

Ostalo

Želiš da pročitaš svih 271 strana?

Slični dokumenti

Forenzički značaj analize morfijuma

Gospodarstvo BiH

Sociologija skripta

Preduzetnicka ekonomija

uvod u pravo

Skripta sociologija za pravni fakultet

Nuklerana medicina

Erp sistemi

Društvo spektakla

Timski rad u projektnim aktivnostima na primeru kompanije Nordeus

Rendgenska analiza proteina: kristalizacija i analiza strukture lizozima

Plan rada ASAP 2024

Bosna srednji vijek

Analiza osnovnih funkcija menadžmenta na primeru preduzeća Swisslion-Takovo d.o.o.

Makroekonomska ravnoteža

Rešeni zadaci iz mehanike: zakon o promeni kinetičke energije i količine kretanja

Zeoliti: struktura, osobine i primena

Istraživanje kao instrument odlučivanja

Prva faza uvođenja AMI/MDM sistema u JP EPS

Analiza propisa u oblasti bezbednosti saobraćaja

SISTEMSKI SOFTVER- OPERATIVNI SISTEM

Organizacija ishrane u bolnici

HEMORAGIJSKE GROZNICE

Merenje telesne temperature

KARAKTERISTIKE STARENJA I SPECIFICNOSTI BOLESTI U STAROSTI

Sida: etiologija, epidemiologija, klinička slika, dijagnostika, lečenje i prevencija

NESTABILNA ANGINA PEKTORIS

Alkoholizam

Proces upravljanja ljudskih resursa

Procesi komercijalnog poslovanja 1 skripta

UPRAVNO PRAVO I

seminarski

Korelacija izmedju debljine intime i medije karotidnih arterija i aktivnosti bolesti u reumatoidnom artritisu

GUILLAIN-BARRE SINDROM

Tradicionalna primjena ljekovitih biljnih vrsta na podrucju opcine Tutin

Radioaktivnost

Policijski stres

Najvisja odlikovanja Republike Srbije

Najvisja odlikovanja Republike Srbije

KOMUNIKOLOGIJA

SIMULACIJA

Regresiona analiza: statistički metod modeliranja odnosa

Linearni trend: analiza i primena u statistici

Komunikologija

TEORIJA ODLUCIVANJA

Biznis plan – Prodavnica autodijelova

Turbine: konstrukcija, podela i primena u energetici

Diplomatsko i konzularno pravo

Finansijko izvjestavanje i poslovno odlucivanje

INTERSTERALEN PROSTOR I MEGJUZVEZDENA MATERIJA

Mikobakterije

Znacaj upravljanja organizacionim promenama

Primena elemenata sportskih igara u mlađem školskom uzrastu

Projektni pristup obrade sadržaja iz upoznavanja okoline

Pojam, uloga, karakteristike i značaj tradicionalnih organizacionih struktura: primer kompanije “Siemens”

Pojam i značaj logistike u špediciji

Razvoj komunikacionih veština dece sa oštećenjem sluha u predškolskim ustanovama

Subjekti za borbu protiv organizovanog kriminaliteta

Osnovne odlike menadžera i njegova uloga pri donošenju poslovnih odluka: primer kompanije „apple“

Aktivnosti u prirodi i njihov značaj u upoznavanju okoline

Tip dokumenta

Oblasti

Popularni predmeti

Institucije