
Elektrotehnika sa elektronikom Pregled
Elektrotehnika sa elektronikom nerecenzirana skripta
1
1. Borov model atoma
Prvi pokušaj objašnjenja strukture atoma poti
č
e od Ernesta Raderforda koji je na osnovu
drugih osobina materije pretpostavio da se atom sastoji od pozitivno naelektrisanog jezgra
oko kojeg kruže negativno naelektrisani elektroni, sli
č
no kretanju planeta oko Sunca (model
se zato i naziva
planetarni model atoma
). Ulogu centripetalne sile u ovom slu
č
aju preuzima
privla
č
na elektrostati
č
ka (Kulonova) sila. Prema znanjima klasi
č
ne elektrodinamike, ve
ć
tada
je bilo jasno da ovaj model ne odgovara realnosti: elektron koji se kružno kre
ć
e neprestano
emituje elektromagnetske talase, pa iako bi to objasnilo zašto elektron zra
č
i svetlost, nije
moglo da objasni strukturu spektra atomskih gasova. Me
đ
utim, klju
č
ni problem ove teorije je
to što bi elektron morao da zra
č
enjem gubi energiju i na kraju "padne" na jezgro.
1913, danski fizi
č
ar Nils Bor (1885-1962) uspeva da objasni spektar atoma vodonika uvode
ć
i
u planetarni model dopunske pretpostavke - postulate, inspirisane uspesima kvantnih hipoteza
Planka i Ajnštajna. Znaju
ć
i da atomi mogu apsorbovati svetlosnu energiju samo u kvantima,
on pretpostavlja da atomi tu energiju mogu tako
đ
e i emitovati samo u kvantima. Time cela
slika o emitovanju i apsorbovanju svetlosti postaje konzistentna.
Bor prihvata planetarni model atoma za osnovu, i pretpostavlja da se pri emitovanju jednog
kvanta svetlosti (fotona) energija atoma smanjuje tako što se smanjuje energija nekog
elektrona u omota
č
u atoma; sa druge strane, pri apsorbovanju jednog kvanta svetlosti (fotona)
se pove
ć
eva energija nekog elektrona u omota
č
u atoma. Ta pretpostavka je objasnila
dotadašnja otkri
ć
a o apsorpciji i emisiji svetlosti kao kvantnim doga
đ
ajima i povezala ih sa
strukturom atoma. Frekvenca emitovanog ili apsorbovanog fotona odre
đ
ena je zakonom o
održanju energije:
E
fot
= h f = E
kr
- E
po
č
E
fot
... energija emitovanog ili apsorbovanog fotona
h ..... Plankova konstanta (6.626 x 10
-34
Js)
f ..... frekvenca svetlosti
E
kr
... energija elektrona na kraju procesa
E
po
č
... energija elektrona na po
č
etku procesa
Klju
č
ni element Borove teorije je povezan sa objašnjenjem strukture spektara atoma: budu
ć
i
da je eksperimentalno utvr
đ
eno da atomi emituju samo odre
đ
ene talasne dužine (samo
odre
đ
ene frekvence), na osnovu prethodnih razmatranja Bor pretpostavlja da elektroni u
atomu mogu imati samo neke vrednosti energije, i da je to zato što elektroni u atomu mogu da
se kre
ć
u samo po nekim putanjima. To Bor povezuje sa mogu
ć
noš
ć
u da elektroni pri kretanju
na tim orbitama ne zra
č
e elektromagnetsku energiju, dok na svim drugim orbitama zra
č
e i ne
mogu trajno da opstanu (kako je to ve
ć
bilo jasno u Raderfordvom modelu). Te orbite Bor
naziva
stacionarnim
. Time Bor pretpostavlja da se kvantuje kretanje unutar atoma, jer ako se
elektroni mogu kretati samo po odre
đ
enim orbitama, onda se mogu kretati samo odre
đ
enim
brzinama, imati samo odre
đ
ene vrednosti energije, i uopšte sve fizi
č
ke
veli
č
ine vezane za
procese u atomu mogu imati samo odre
đ
ene - kvantovane - vrednosti. Time je promenjen
pogled na celokupnu fiziku i uvedeni su pojmovi
kvantne mehanike
i
kvantne fizike
uopšte.
Veli
č
ina Borovog modela je u tome što on daje i kvantitavni uslov na osnovu koga se mogu
izra
č
unati vrednosti svih tih veli
č
ina Pore
đ
enje sa eksperimentalnim istraživanjima je
pokazalo slaganje koje je potvrdilo Borovu teoriju.
Bor je dao uslov koji orbita mora da ispunjava da bi bila stacionarna: moment koli
č
ine
kretanja elektrona na orbiti mora biti celobrojni umnožak kvanta momenta koli
č
ine kretanja
L
kv
= h/2
π
. Zna
č
i, elektron na prvoj orbiti ima moment koli
č
ine kretanja L
1
= h/2
π
, na drugoj
L
2
= 2 h/2
π
i tako redom. Redni broj orbite na kojoj se nalazi elektron se naziva
glavni
Elektrotehnika sa elektronikom nerecenzirana skripta
2
kvantni broj
elektrona. Borov model me
đ
utim, nije mogao da objasni uzrok kvantovanja:
njegov glavni doprinos se sastojao u uvo
đ
enju kvantnog podgleda na fizi
č
ke objekte.
Povedeni Borovim radom, u slede
ć
ih desetak godina su De Brolji, šredinger, Hajzenberg,
Pauli, Dirak i drugi fizi
č
ari razvili
talasnu kvantnu mehaniku
, pogled na mikrosvet u kome je
od klju
č
nog zna
č
aja pretpostavka da celopkupna materija ima i talasna i
č
esti
č
na svojstva. U
talasnoj kvantnoj mehanici, elektroni u stacionarnom stanju u atomu predstavljaju svojevrsne
stoje
ć
e talase, a Borov kvantni uslov predstavlja uslov nastajanja stoje
ć
eg talasa u zatvorenom
prostoru.
Sl. 1.1Bohrov model atoma.
2. Kulonova sila
(
Charles Augustin Koulon 1736-1860)
sin je pravnika iz Langedoka, inspektora
kraljevskih dobara .Majka je želela da bude lekar , a on se oduševljavao
matematikom.Kulon napušta majku i završava studjie-inženjersku školu u Mezijeu.
-Kulon primenjuje dinami
č
ki metod oscilacija gde je izvo
đ
enje eksperimenta lakše
ali je interpretacija ekspeimenta teža .Horinzontalna igla obešena o konac
usmerena je ka centru sfere i na kraju prema sferi ima malu plo
č
u naelektrisanu
suprotno naelektrisanju sfere .Kada se pomakne iz stabilnog položaja ona oscilira.
•
Dva naelektrisana tela (
) se medjusobno privla
č
e ili odbijaju silom koja je
srazmerna proizvodu njihovog naelektrisanja, a obrnuto srazmerna kvadratu
rastojanja izmedju ta dva tela.
•
2
2
1
0
4
1
r
q
q
F
•
Pri
č
emu je:
•
F
- Elektri
č
na sila,
•
k
- Kulonova konstanta (zavisi od sredine u kojoj se tela nalaze),
•
q
1
i
q
2
- Naelektrisanja tih tela,
•
r
- Rastojanje izme
đ
u tih tela "
Karakter Kulonove sile zavisi iskljucivo od prirode naelektrisanja.

Elektrotehnika sa elektronikom nerecenzirana skripta
4
Linije elektri
č
nog polja sa vektormo polja kao tangentnom
SPEKTAR LINIJA ELEKTRI
Č
NOG POLJA. Privla
č
no odbojni karakter elektri
č
nog polja. Kao što
smo rekli linije elektri
č
nog polja su orijentisane linije sa izvorima na površini pozitivnih
optere
ć
enja i ponorima na površinama negativnih optere
ć
enja
.
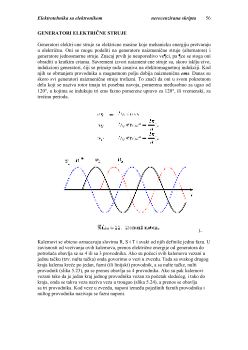
5.Rad sila elektricnog polja
Ako se u elektri
č
no polje unese probno optere
ć
enje
q, na njega polje deluje silom
E
q
F
Pod dejstvom te sile, optere
ć
enje
q se kre
ć
e po odre
đ
enoj putanji (recimo od ta
č
ke M do
ta
č
ke N), pri
č
emu rad vrše sile elektri
č
nog polja. U opštem slu
č
aju je sila F promenljiva i
po intezitetu, pravcu i smeru rad koji s tom prilikom izvrši bi
ć
e
l
F
A
Ukupni rad sile F po celoj putanji bi
ć
e jednak
N
M
N
M
Edl
q
Fdl
A
Integral koji stoji uz
q predstavlja linijski integral vekotra elektri
č
nog polja E na putanji
M-N.
Elektrotehnika sa elektronikom nerecenzirana skripta
5
Elektrostati
č
ko polje pripada klasi
konzervativnih polja
. Karakteristika konzervativnih
polja jeste da je rad sila u ovim poljima po zatvorenoj putanji jednak nuli. Drugim re
č
ima
rad koji izvrše sile polja E pri pomeranju probnog optere
ć
enja duž neke zatvorene
putanje, ne zavisi od oblika putanje ve
ć
samo od položaja njenih krajnjih ta
č
aka.
6. Elektri
č
ni potencijal
•
Elektri
č
ni potencijal (znak:
φ
ili
U
) veli
ina je u fizici i elektrotehnici kojom
se izražava elektri
č
na potencijalna energija optere
ć
Pri tome je ja
č
ina elektri
č
nog polja jednaka negativnom gradijentu elektri
č
nog
potencijala:
•
Elektri
č
ni se potencijal ne može neposredno meriti, ve
ć
se meri samo njegova
razlika koja je jednaka elektri
•
ke u prostoru u kojima elektri
č
ni potencijal ima jednake vrednosti
č
ine
ekvipotencijalne površine.
•
SI mernih jedinica propisuje za elektri
č
ni potencijal izvedenu jedinicu volt.
Posmatrajmo probno optere
ć
enje u ta
č
ki A (x
0
,y
0
, z
0
) u prostoru. Probno
optere
ć
enje raspolaže u odnosu na neku ta
č
ku P (x
1
,y
1
,z
1
) potencijalniom
energijom Wp, koja je jednaka radu koji treba da izvrše sile polja da bi
optere
ć
enje
q prebacili iz ta
č
keM u ta
č
ku P. Prema tome
W
P
= A=
Fdl=
q
E
l
Ova potencijalna energija zavisi od
q i položaja pomenutih ta
č
aka, i ne zavisi od
puta koji povezuje ove dve ta
č
ke. Koli
č
nik potencijlane energije i probnog
optere
ć
enja je nazavisan od probnog optere
ć
enja i definiše elektrostati
č
ki
potencijal ( ili elektir
č
ni skalar potencijal)
M
Edl
Ova funkcija je skalrane prirode i opisuje elektri
č
no polje na ekvivalentatan na
č
in
kao i funkcija E.
Razlika potencijala izme
đ
u dve ta
č
ke M i N predstavlja napon U
M-N
.
U
M
N =
N
M
Edl
7. Potencijal ta
č
kastog optere
ć
enja i skupa ta
č
kastih optere
ć
enja
Pošto nam je od ranije poznato da je
M
Edl
0
2
0
4
1
r
r
Q
E
Integrale
ć
i gornji izraz u datim granicama dobijamo kona
č
ni izraz za potencijal ta
č
kastog
optere
ć
enja sa referentnom ta
č
kom u beskona
č
nosti u obliku:
M
M
r
Q
l
d
E
1
4
0
Elektrotehnika sa elektronikom nerecenzirana skripta
7
na onim delovima površine gde linije elektr
č
nog polja u ulaze u provodnik, a pozitivna na
onim delovima površine gde linije polja napuštaju provodnik. Pojava razdvajanja pozitivnih i
negativnih optere
đ
enja pod dejstvom spoljašnjeg elektri
č
nog polja naziva se elektrostati
č
ka
indukcija.
Pošto je provodnik pre unošenja u polje bio elektr
č
no neoptere
ć
en, sumarno optere
ć
enje posle
unošenja mora biti jednako nuli..Indukovana optere
ć
enja se raspore
đ
uju tako da njihov polje
poništava primarn strano polje u unutrašnjosti i u
č
ini da rezultuju
ć
i vektor polja na spoljašnjoj
površini provodnika bude normalan na nju. Na taj na
č
in u unutrašnjosti provodnika nema
polja. Još jednom nagalšavamo da linije polje ulatze odnosno izlaze sa površine provodnika
pod pravim uglom. Ista siutacija je i u slu
č
aju kada u prosotr polja unesemo šupalj provodnik.
Površinska naelektrisanja se lokalizuju u veoma tankom površinskom sloju odnosno dolazi do
ekrnizuju
ć
eg dejstva šupljih provodnika i posotji samo u slu
č
aju polja koja poti
č
u od
spolja
č
njih optere
ć
enja (Faradejev kavez).
10. Raspodela optere
ć
enja na površini provodnika efekat šiljka.
11.Neki primeri raspodele polja kod simetri
č
nih tela kona
č
nih dimenzija
Želiš da pročitaš svih 77 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































