VISOKA ŠKOLA
CENTAR ZA POSLOVNE STUDIJE
KISELJAK
RADOSLAV MILETIĆ
KODIRANJE
SEMINARSKI RAD
Kiseljak, 2014. godine
VISOKA ŠKOLA
CENTAR ZA POSLOVNE STUDIJE
KISELJAK
KODIRANJE
SEMINARSKI RAD
PREDMET: INFORMACIJSKI SUSTAVI U CESTOVNOM PROMETU
MENTOR: mr sc HADŽIB SALKIĆ
STUDENT: RADOSLAV MILETIĆ
BROJ INDEKSA: 19/2011
ODSIJEK: CESTOVNI PROMET
Kiseljak, februar 2014. godina
0
UVOD
Kompjuter razumije samo binarni jezik, jezik koji se sastoji od dva simbola,
„0“ i „1“. Unutar kompjutera znakovi su prikazani pomoću binarnih brojeva.
Postupak pripisivanja simbola znakovima vanjskog svijeta naziva se kodiranje. Skup
takvih simbola naziva se kod. Kod je u najširem smislu sustav znakova pomoću
kojeg sudionici komunikacije
komuniciraju
. Svaki kod da bi bio kodom mora imati
popis
svih znakova,
propis
po kojem se ti znakovi slažu i opis tih znakova.
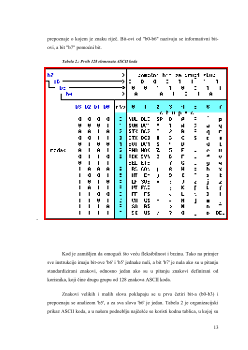
Kodni sustav je dogovor o načinu kodiranja. Najrasprostranjeniji kodni sistem
je ASCII kod ( kratica od: American standard code for information intercharge).
Svaki simbol i znak je predočen jednim sedmero znamenkastim binarnim brojem, a
ukupno je na raspolaganju 2
7
=128 znakova. Postoji i proširen, osambitovni ASCII u
kojem se prvih 128 znakova koristi kao i u osnovnom ASCII-u, a preostalih 128
znakova se koristi za slova različitih zemalja, pa postoji mnogo različitih proširenih
ASCII normi.
Najpoznatiji kodovi su
Marconi-kod
,
Morseov kod
, Q-kod i Z-kod, a jedan od
najkompliciranijih kodova koji je ikad bio korišten je
njemački
tajni kod
Enigma
iz
II. SR
, čije otkrivanje i rješavanje je u mnogome promijenilo tok rata i ubrzalo
njegov kraj.
U prvom poglavlju biće predstavljen sam pojam koda i kad je nastao.
U drugom poglavlju ćemo objašnjavati kodiranje koje će biti predstavljeno i
kroz bromjere i tabele.
Treće poglavlje govori o tetradnim kodovima i njenoj podjeli, dok je četvrto
poglavlje bazirano na ASCII kod i njegove vrste i primjere.
Peto i šesto poglavlje objašnjava EBCDI KOD I UNI KOD.
1. KOD
Kodovi su nastali u srednjem vijeku. U istoriji se spominju kodovi još iz XIII.
i XIV vijeka, koji su primjenjivani u nekim talijanskim državama. I Dubrovačka
Republika je imala neke slične šifre. Disciplina koja se bavi proučavanjem i
otkrivanjem kodova i šifri zove se kriptografija.
Pretpostavka uspješnog komuniciranja kompjutera u razmjeni ili obradi
podataka je dogovor o skupu znakova koji će se u radu s kompjuterom koristiti te
pripadajućim binarnim kombinacijama za svaki od znakova i zadaći koja se za
svakog ima izvršiti. Onaj ko se ne drži dogovora ne može komunicirati s ostalima
koji poštuju taj dogovor. Dogovor se vremenom proširuje i nadograđuje, i može
postati ozakonjen standard države ili preporuka neke međunarodne organizacije.
Navedeno nije pojam koji je vezan uz zaštitu podataka (
kriptiranje
), već se odnosi
isključivo na međusobnu komunikaciju između kompjutera, odnosno njihovih
korisnika. Skup svih znakova (grafema) koji se koriste u komunikaciji naziva se
apstraktna abeceda, koja zajedno s pripadajućim binarnim (ili nekim drugim)
kombinacijama stvara kod. Znak u kodu naziva se kodni element, a pripadni mu
zamjenitelj, bilo da je u pitanju binarna kombinacija, neki drugi znak ili nešto treće,
naziva se kodna zamjena.
Kod je u najširem smislu sistem znakova pomoću kojeg sudionici
komunikacije (najmanje dva) komuniciraju. Svaki kod da bi bio kodom mora imati
popis svih znakova, propis po kojemu se ti znakovi slažu i opis tih znakova. Kod je
vrsta šifre kod koje se riječi, rečenice, dijelovi riječi i rečenica, slova i brojevi
otvorenog teksta zamjenjuju grupama slova ili brojeva - kodnim zamjenama. Kodovi
se najčešće izrađuju u obliku riječnika. Sadrže nekoliko desetina hiljada otvorenih
izraza, od kojih svaka ima po jednu ili više kodnih zamjena, skupine od po 2, 3, 4 ili
5 slova ili brojeva. Kao i ostale vrste šifri i kodovi su namijenjeni osiguranju tajnosti
sadržaja povjerljive poruke (vojne, diplomatske i druge). Kodom se postiže i
skraćivanje teksta.
2. OSNOVE TEORIJE KODIRANJA I DEKODIRANJA
2
Kod dekadnog brojnog sistema brojimo "nula, jedan, dva, tri, četiri, pet, šest,
sedam, osam, devet, deset", a "deset" je u suštini "0 jedan dalje". Analogno
navedenom može se izgraditi binarni sistem brojeva prema primjeru u tablici.
0 0 1 1 Slijedi „0 jedan dalje“ 2 10 3 11 Slijedi „00 jedan dalje“ 4 100 5 101 6 110
7 111 Slijedi „000 jedan dalje“ 8 1000 ... ...
Opšti oblik za pretvaranje binarnog broja u dekadni je:
1 2 1 0 10 *2
n
*2
n
... *2 *2 *2
N a a a a a
− = + + + + +
- N je broj brojnog sistema izražen znamenkama „
a
“, - a znamenke sistema: „
0
“ ili
„
1
“, - 2 je baza (osnova) brojnog sistema.
2.2. Pretvaranje dekadnog broja u binarni broj
Pretvaranje dekadnog broja u binarni broj može se izvršiti na dva načina:
dijeljenjem s 2 ili
pomo
ć
u tabela.
Pretvaranje, dijeljenjem sa dva je postupak koji se može primijeniti za
pretvaranje dekadnih brojeva, u brojeve bilo kojeg sistema, dijeljenjem sa osnovicom
tog sistema. Pretvaranje dijeljenjem s dva, vrši se sukcesivnim dijeljenjem s 2.
Ostatak dijeljenjem predstavljaju brojke 0 ili 1. Kad se dijeljenjem dođe do operacije
1 : 2 = 0 i 1 ostatak, dijeljenje je završeno. Čitanje rezultata vrši se odozdo prema
gore. Na ovaj način se vrši pretvaranje cijelih brojeva dekadnog brojnog sistema u
binarni brojni sistem.
Primjeri:
(125)10 = ( )2
125 : 2 = 62 Ostatak
1
62 : 2 = 31 “
0
31 : 2 = 15 “
1
15 : 2 = 7 “
1
7 : 2 = 3 “
1
3 : 2 = 1 “
1
1 : 2 = 0 “
1
Čitanje:
(125)10 = (1111101)2
4
