71
3.
LINIJSKI ELEMENTI
3.1.
3.1.
3.1.
3.1.
GREDNI NOSAČI
GREDNI NOSAČI
GREDNI NOSAČI
GREDNI NOSAČI
3.1.1.
3.1.1.
3.1.1.
3.1.1.
KARAKTERISTIKE, PRIM
KARAKTERISTIKE, PRIM
KARAKTERISTIKE, PRIM
KARAKTERISTIKE, PRIMENA I SISTEMI
ENA I SISTEMI
ENA I SISTEMI
ENA I SISTEMI
Grednim nosačima smatramo one linijske elemente koji su pretežno opterećeni na savijanje
silama. Javljaju se sastavnim delom praktično svih inženjerskih konstrukcija i najčešće su
horizontalnog pravca pružanja.
U zgradarstvu se primenjuju kao noseći elementi meñuspratnih konstrukcija, kao glavni
nosači krovnih konstrukcija većeg raspona, kao sastavni deo temeljnih konstrukcija
(temeljne kontragrede). Kod mostova grednog sistema primenjuju se kao glavni isekundarni
nosači mostovske konstrukcije. Pojavljuju se i kao sastavni deo složenijih armiranobetonskih
elemenata: rigle ramovskih konstrukcija, gredni nosači kombinovanih sistema, osnovni
elementi temeljnih roštilja itd. U konstrukcijama se gredni elementi najčešće javljaju u
sklopu sa drugim elementima: stubovima, pločama, zidovima (Sl. 77).
Sl. 76.
Statički sistemi grednih nosača
Načelno, gredni nosači mogu biti projektovani preko jednog ili više raspona. Statički sistem
grednog nosača je odreñen rasporedom oslonaca, koji mogu biti formirani kao nepomerljivi
ili pomerljivi (potpuno, delimično). Reñi je slučaj da je greda na svom jednom kraju
uklještena u masivni zid ili neki drugi element konstrukcije. U konstrukcijama zgradarstva su
najčešće kruto vezane za vertikalne oslonce (stubove), čime se formiraju armiranobetonski
okviri (Sl. 76).
Sl. 77.
Okvirne i roštiljne konstrukcije
3. Linijski elementi
73
Sl. 79.
Vertikalne i horizontalne vute
Jedna vrsta horizontalne vute se često primenjuje u oslonačkim delovima grednih elemenata
(posebno karakteristično za montažne grede), kada se proširenjem preseka povećava moć
prijema glavnih napona zatezanja, koji u ovim zonama imaju maksimalne vrednosti (Sl. 80).
U konkretnoj situaciji, uobičajeno je proširenje rebra na širinu uže (donje) flanše.
Sl. 80.
Oblikovanje oslonačkog dela grede nesimetričnog I-preseka
Sl. 81.
Montažna greda promenljive visine
Osim vutama, promenljiva silueta može biti izvedena i promenom visine nosača duž cele
njegove dužine, na primer. Takav je slučaj kod krovnih grednih glavnih nosača, kada se
gornja ivica projektuje u nagibu, kojim je greda opskrbljena maksimalnim visinama preseka
na mestima maksimalnih momenata savijanja, a, sa druge strane, obezbeñen nagib za
krovne ravni (Sl. 81).
3.1.3.
3.1.3.
3.1.3.
3.1.3.
PRORAČUN
PRORAČUN
PRORAČUN
PRORAČUN UTICAJA
UTICAJA
UTICAJA
UTICAJA
Proračun statičkih uticaja grednih nosača se, načelno, sprovodi saglasno linearnoj teoriji
elastičnosti. Pri tome, za raspon grede se usvajaju odgovarajuća rastojanja sistemskih linija.
Meñutim, kada je širina oslonca veća od desetina raspona grede, ili kada nije moguće utvrditi
položaj sistemnih linija, teorijski raspon grede (raspon grede u statičkom sistemu) može se
usvojiti kao svetli raspon uvećan za 5%.
Sa ovako usvojenim rasponima formira se statički sistem nosača, za koji se odreñuju uticaji.
Iako je uobičajeno da se, za gredne elemente u konstrukcijama zgradarstva, uticaji odreñuju
za ukupno opterećenje
25
. Ipak, kad god to može dovesti do značajnijih promena u
25
Razlog je relativno mali udeo korisnog tereta u ukupnom u konstrukcijama zgradarstva.
Brujić - Betonske konstrukcije – radna verzija - 9. avgust 2011
74
rezultatima, neophodno je razmatrati različite rasporede korisnog opterećenja (skladišta,
biblioteke, sportski objekti...), te eventualnu povoljnost delovanja pojedinih dejstava (različiti
rasponi kod kontinualnih nosača, na primer).
Sl. 82.
Teorijski rasponi grednog nosača
Kod kontinualnih greda, bez obzira na rezultat odreñivanja statičkih uticaja, prilikom
dimenzionisanja je, za pozitivne momente u polju, neophodno usvojiti vrednosti najmanje
jednake onima koje odgovaraju mometima u polju obostrano, odnosno jednostrano,
uklještene grede opterećene ravnomerno podeljenim opterećenjem (Sl. 83).
Sl. 83.
Minimalne „proračunske“ vrednosti momenata u polju kontinualne grede
Uklještenje nad krajnjim osloncem kontinualne grede je opravdano usvojiti u statičkom
sistemu samo kada je ono konstruktivnim merama obezbeñeno i dokazano. Kontinualne
grede oslonjene na zidove ili stubove od opeke, kada rotacija grede nije sprečena, dakle, nad
osloncima treba dimenzionisati prema redukovanoj, paraboličnoj raspodeli momentnog
dijagrama (Sl. 84a). Češći slučaj je kruta veza grede sa stubovima, kada je opravdano
oslonački presek grede dimenzionisati na momente na ivici oslonca (Sl. 84b).
Sl. 84.
Oslonački momenti kod kontinualnih greda zglobno i kruto spojenih sa osloncima
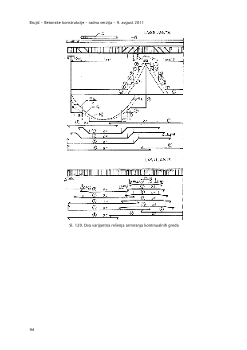
Sl. 85.
Dijagrami momenata savijanja u grednim nosačima
Prikazani su (Sl. 85) karakteristični oblici dijagrama momenata savijanja za najčešće statičke
sisteme (prosta greda, kontinualna greda, okvir) u kojima se nalaze gredni elementi.
Načelno, greda kod koje je nad krajnjim osloncima ostvareno delimično ili potpuno
Brujić - Betonske konstrukcije – radna verzija - 9. avgust 2011
76
3.1.3.1.
3.1.3.1.
3.1.3.1.
3.1.3.1.
Preraspodela momenata savijanja
Preraspodela momenata savijanja
Preraspodela momenata savijanja
Preraspodela momenata savijanja i duktilnost preseka
i duktilnost preseka
i duktilnost preseka
i duktilnost preseka
Statički uticaji kod statički neodreñenih konstrukcija su funkcija krutosti elemenata i njihove
promene. Krutosti po dužini armiranobetonskih elemenata se menjaju u skladu sa
dostignutim naponsko-deformacijskim stanjem, isprskalošću preseka, promenom količine
armature... Na Sl. 87 su prikazana karakteristična naponsko-deformacijska stanja grednog
elementa opterećenog dvema koncentrisanim silama. Malim momentima savijanja odgovara
pravolinijska raspodela normalnih napona (I
a
), i u pritisnutom i u zategnutom delu.
Momentima neposredno pred pojavu prslina (I
b
) odgovara linearno promenljivo naponsko
stanje u pritisnutoj i nelinearno promenljivo u zategnutoj zoni. Za momente jednake i veće
od momenta pojave prsline, javljaju se prsline (na ovim mestima je zatežući normalni napon
u betonu jednak nuli), a raspodela napona pritiska po visini pritisnute zone je kvazi-linearna
(II). Daljim povećanjem opterečenja, šire se prsline, zategnuta podužna armatura je u
plastičnoj fazi rada, a pritisnuti beton trpi nelinearne deformacije, zbog čega se i naponski
dijagram odlikuje visokom nelinearnošću (III). Ovo stanje, stanje III, odgovara graničnom
kapacitetu nosivosti preseka i koristi se za proračun preseka prema graničnoj nosivosti.
Sl. 87.
Karakteristična naponsko-deformacijska stanja grednog elementa
Uticaji odreñeni primenom linearne teorije elastičnosti su, kod armiranobetonskih elemenata
u statički neodreñenim konstrukcijama, „realni“ samo za male nivoe opterećenja. Razvoj
prslina i plastifikacija u čeliku za armiranje mogu, nekad, kvalitativno da promene stanje
naprezanja elementa. I pored toga, linearna teorija elastičnosti, odnosno uticaji odreñeni
njenom primenom, se koristi i za uticaje u stanju granične nosivosti. Kasnije, prilikom
dimenzionisanja poprečnih preseka, uvažavaju se činjenice nelinearnog deformisanja, ali sa
uticajima koji, još jednom, odgovaraju linearnoj teoriji elastičnosti.
Postavlja se pitanje koliko ovakva nedoslednost može biti održiva i opravdana. Sa stanovišta
jednostavnosti primene, nema dileme da je prednost na strani ovakvog pristupa. Ali, čak i
kad je opravdanost u pitanju, ovakav koncept je održiv. Naime, rezultati linearne teorije
elastičnosti predstavljaju jedno moguće ravnotežno stanje statički neodreñene konstrukcije.
Konstrukcija (i elementi) dimenzionisani i armirani saglasno ovim uticajima će se u velikoj
meri i ponašati na ovaj način. Posledica je ovo, pre svega, činjenice da se, kolokvijalno,
„armiranobetonski elementi ponašaju na način na koji su armirani“. Ovo ne znači da se u
tako armiranoj konstrukciji neće realizovati preraspodele naprezanja, naravno, ali svakako
ne u istoj meri u kojoj bi to bio slučaj da je sa ovakvim preraspodelama kalkulisano.
