studenti.rs home page

Uvod

Metod zamene

Metod suprotnih koeficijenata

Grafi ˇcki metod

Re ˇsavanje sistema jedna ˇcina u fizici

Sistemi linearnih jednaˇcina sa dve nepoznate

31. mart 2011.

Sistemi linearnih jedna ˇcina sa dve nepoznate

Uvod

Metod zamene

Metod suprotnih koeficijenata

Grafi ˇcki metod

Re ˇsavanje sistema jedna ˇcina u fizici

1

Uvod

2

Metod zamene

3

Metod suprotnih koeficijenata

4

Grafiˇcki metod

5

Reˇsavanje sistema jednaˇcina u fizici

Reˇsavanje sistema metodom zamene
Reˇsavanje sistema metodom suprotnih koeficijenata
Reˇsavanje sistema grafiˇckom metodom

Sistemi linearnih jedna ˇcina sa dve nepoznate

background image

Uvod

Metod zamene

Metod suprotnih koeficijenata

Grafi ˇcki metod

Re ˇsavanje sistema jedna ˇcina u fizici

Uvod

Definicija

Linearna jednaˇcina sa dve nepoznate

x

i

y

je svaka jednaˇcina ekvivalentna

jednaˇcini oblika

ax

+

by

+

c

=

0

, gde su

a

,

b

,

c

realni brojevi, a koeficijenti

a

i

b

ne mogu istovremeno biti

0

.

Definicija

Reˇsenje linearne jednaˇcine sa dve nepoznate

ax

+

by

+

c

=

0

je svaki

uredjeni par

(

x

0

,

y

0

)

koji zamenom

x

sa

x

0

i

y

sa

y

0

tu jednaˇcinu prevodi u

taˇcnu brojevnu jednakost.

Sistemi linearnih jedna ˇcina sa dve nepoznate

Uvod

Metod zamene

Metod suprotnih koeficijenata

Grafi ˇcki metod

Re ˇsavanje sistema jedna ˇcina u fizici

Uvod

Definicija

Opˇsti oblik sistema od dve linearne jednaˇcine sa dve nepoznate

x

i

y

je:

a

1

x

+

b

1

y

+

c

1

=

0

a

2

x

+

b

2

y

+

c

2

=

0

gde su

a

1

,

b

1

,

c

1

,

a

2

,

b

2

,

c

2

realni brojevi.

Definicija

Reˇsenje sistema od dve linearne jednaˇcine sa dve nepoznate

x

i

y

je svaki

uredjeni par realnih brojeva

(

x

0

,

y

0

)

koji je reˇsenje obe jednaˇcine sistema.

Sistemi linearnih jedna ˇcina sa dve nepoznate

background image

Uvod

Metod zamene

Metod suprotnih koeficijenata

Grafi ˇcki metod

Re ˇsavanje sistema jedna ˇcina u fizici

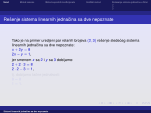
Reˇsenje sistema linearnih jednaˇcina sa dve nepoznate

Tako je na primer uredjeni par relanih brojeva

(

2

,

3

)

reˇsenje slede´ceg sistema

linearnih jednaˇcina sa dve nepoznate:

x

+

2

y

=

8

2

x

−

y

=

1

,

jer smenom

x

sa

2

i

y

sa

3

dobijamo:

2

+

2

·

3

=

8

2

·

2

−

3

=

1

,

tj. dobijamo taˇcne jednakosti:

8

=

8

1

=

1

.

Sistemi linearnih jedna ˇcina sa dve nepoznate

Želiš da pročitaš svih 29 strana?

Prijavi se i preuzmi ceo dokument.

Prijavi se Napravi nalog

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.

Slični dokumenti