GRA EVINSKI FAKULTET
SVEU ILIŠTA U RIJECI
SKRIPTA RIJEŠENIH ZADATAKA IZ
OTPORNOSTI MATERIJALA
NEIRA TORI
,
dipl.ing.gra .
2
1. Zadatak
Izra unati naprezanja i nacrtati dijagram naprezanja na konzolnom nosa u ako je zadano :
2
2
1
1
1
1
mm
N
MPa
m
N
Pa
=
=
Vrijednosti uzdužnih sila na pojedinim segmentima :
N
F
N
F
F
N
N
F
N
I
II
III
4
3
2
1
4
1
10
4
0
10
2
⋅
=
=
=
+
−
=
⋅
−
=
−
=
Vrijednosti naprezanja na pojedinim segmentima :
MPa
Pa
A
N
A
N
MPa
Pa
A
N
I
I
II
I
III
III
40
10
40
0
20
10
20
6
6
=
⋅
=
=
=
=
−
=
⋅
−
=
=
σ
σ
σ
m
b
m
a
m
cm
A
Pa
E
N
F
N
F
F
1
2
10
10
10
2
,
2
10
4
10
2
2
3
2
11
4
3
4
2
1
=
=
=
=
⋅
=
⋅
=
⋅
=
=
−
4
3. Zadatak
Odrediti pomak to ke C ukoliko se temperatura štapa 1 pove a za T :
Rješenje :
β
δ
=
β
δ
=
β
∆
α
=
β
∆
=
δ
=
∆
δ
∆
=
β
∆
α
=
ε
=
∆
⇒
∆
=
ε
sin
v
cos
u
2
sin
Tl
2
sin
l
0
l
;
l
2
sin
Tl
l
l
l
l
C
C
1
C
2
C
1
t
t
t
t
5
4. Zadatak
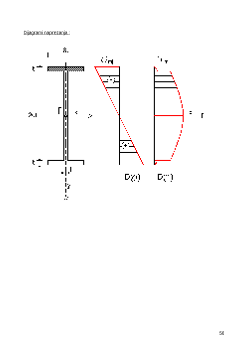
Odrediti naprezanja u štapovima ukoliko se temperatura štapa 2 pove a za T :
Rješenje
Iz plana pomaka i optere enja (ovdje promjena
temperature) možemo zaklju iti da se štap 2 nastoji
izdužiti, no njegovo potpuno izduženje sprje avaju druga
dva štapa spojena u voru D, koji nisu direktno optere eni i
nemaju tendenciju izduženja. Štap 2 se izduži za l
t
pri
2
D' u D''.
Budu i da su sva tri štapa me usobno spojena u voru D,
izduženjem štapa 2 prisilno se izdužuju i štapovi s brojem
1. Kao posljedica izduženja u njima se javlja vla na sila
F
1
(vla na sila uzrokuje izduženje ako nema nikakvog drugog
optere enja).
Zadatak 5
Iz uvjeta ravnoteže sila :
( )
1
0
cos
2
0
2
1
K
=
−
→
=
Σ
F
F
Y
α
Iz plana pomaka :
( )
2
cos
cos
2
1
2
1
1
2
K
α
α
l
l
l
l
l
l
∆
=
∆
→
∆
∆
=
=
Iz Hookovog zakona :
( )
3
1
1
1
1
1
K
A
E
l
F
l
=
∆
( )
4
2
2
2
2
2
2
2
K
l
T
A
E
l
F
l
⋅
∆
⋅
+
=
∆
α
( )
( )
α
α
α
3
2
2
1
1
2
1
1
2
1
cos
2
1
cos
)
2
(
4
);
3
(
;
1
A
E
A
E
A
TE
F
−
∆
=
⇒
→
α
α
α
α
3
2
2
1
1
3
1
1
2
2
1
2
cos
2
1
cos
2
cos
2
)
1
(
A
E
A
E
A
TE
F
F
F
−
∆
=
⇒
=
→
2
2
2
1
1
1
;
A
F
A
F
−
=
=
σ
σ
7
6. Zadatak
Odrediti naprezanja u štapovima 1 i 2 te vertikalni pomak to ke D.
Rješenje
Sustav je jedanput stati ki neodre en (ima jednu prekomjernu veli inu), odnosno nepoznate su
4 veli ine ( R
H
, R
V
, S
1
, S
2
).
Uz tri uvjeta ravnoteže postavljamo dodatnu jednadžbu na deformiranom sustavu na principu
sli nosti trokuta.
Iz uvjeta ravnoteže sila :
( )
( )
( )
3
0
sin
0
2
cos
0
cos
0
1
0
sin
0
1
2
1
1
1
1
2
2
K
K
K
=
+
+
−
→
=
Σ
=
→
=
−
→
=
Σ
=
−
−
→
=
Σ
V
H
H
A
R
S
F
S
Y
S
R
S
R
X
a
S
a
S
Fl
M
α
α
α
α
Iz plana pomaka :
α
δ
δ
sin
;
1
2
l
l
B
C
∆
=
∆
≡
Iz sli nosti trokuta :
( )
4
1
2
K
a
a
B
C
δ
δ
=
Iz Hookovog zakona :
2
2
2
2
2
1
1
1
1
1
;
A
E
l
S
l
A
E
l
S
l
=
∆
=
∆
( )
4
→
( )
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
2
2
2
2
1
1
2
2
2
1
1
2
2
1
2
1
1
2
2
2
1
1
2
1
sin
1
1
sin
a
A
E
l
l
S
a
l
l
l
a
l
A
S
A
S
a
a
l
l
A
E
A
E
a
Fl
S
S
a
a
l
l
A
E
A
E
S
S
D
D
=
∆
=
⇒
=
∆
=
=
+
=
⇒
→
=
δ
δ
σ
σ
α
α
