
Zbirka zadataka iz fizike za pripremu razredbenih ispita na fakultetima Pregled
Izdava
č
HINUS
Zagreb, Miramarska 13 B
tel. (01) 615 41 96, 6687382, 611 55 18
fax (01) 611 55 18
e-mail [email protected]
Urednik
Mr. sc. Hrvoje Zrn
č
i
ć
Recenzenti
Prof. dr. sc. Ivica Picek
Prof. An
đ
ela Gojevi
ć
ISBN 978-953-6904-28-0
Copyright © Hrvoje Zrn
č
i
ć
Knjigu možete besplatno preuzeti samo za osobnu upotrebu, a ne smijete je
stavljati na druge mrežne stranice, umožavati ili je koristiti za bilo koju
komercijalnu svrhu.

SADRŽAJ
PREDGOVOR
..................................................................................................................7
VAŽNIJE FIZIKALNE KONSTANTE
................................................................8
MEHANIKA
......................................................................................................................9
JEDINICE ZA MJERENJE ....................................................................................................9
GIBANJA DUŽ PRAVCA ...................................................................................................10
OSNOVNI ZAKONI GIBANJA ..........................................................................................14
IMPULS SILE I KOLI INE GIBANJA ..............................................................................15
SLAGANJE I RASTAVLJANJE SILE ................................................................................16
RAD, ENERGIJA, SNAGA..................................................................................................19
SLOŽENA GIBANJA...........................................................................................................22
JEDNOLIKO GIBANJE PO KRUŽNICI.............................................................................25
INERCIJALNI I AKCELERIRANI SUSTAVI....................................................................26
OP I ZAKON GRAVITACIJE............................................................................................27
STATIKA KRUTOG TIJELA ..............................................................................................28
ROTACIJA KRUTOG TIJELA............................................................................................30
HIDROMEHANIKA I AEROMEHANIKA ........................................................................32
PRIMJERI .............................................................................................................................34
HARMONI
Č
KO TITRANJE I VALOVI
...........................................................42
MEHANI KO TITRANJE...................................................................................................42
MEHANI KI VALOVI........................................................................................................44
PRIMJERI .............................................................................................................................47
TOPLINA.....................................................................................................
49
MOLEKULSKI SASTAV TVARI .......................................................................................49
PROMJENA UNUTRAŠNJE ENERGIJE ...........................................................................50
TOPLINSKO RASTEZANJE VRSTIH TVARI ...............................................................52
PROMJENE STANJA PLINA..............................................................................................53
MEHANI KI RAD I UNUTARNJA ENERGIJA ...............................................................56
PRIMJERI .............................................................................................................................57

PREDGOVOR
Ovaj
ć
e priru
č
nik prije svega korisno poslužiti svakom tko se želi
pripremiti za polaganje razredbenog ispita na bilo kojem od fakulteta na
kojem se polaže fizika. Uporaba ovog priru
č
nika i školskih udžbenika iz
fizike za op
ć
u gimnaziju propisanih od fakulteta kao obavezna literatura u
potpunosti je dovoljna da bi se uspješno položio svaki razredbeni ispit iz
fizike.
Priru
č
nik je sastavljen tako da omogu
ć
uje brzo i kvalitetno savlada-
vanje gradiva. U prvom je dijelu priru
č
nika sažet i obra
đ
en teoretski dio
gradiva redom po podru
č
jima. Na kraju svakog podru
č
ja dani su pažljivo
odabrani primjereni zadaci. U drugom dijelu priru
č
nika prikazani su zadaci
zajedno s pripadaju
ć
im rješenjima koji su se pojavljivali na prethodnim
razredbenim ispitima. Iza svakog zadatka odnosno rješenja slijedi i prikaz
kompletnog postupka s neophodnim pojašnjenjima kako se dolazi do rješe-
nja. Ono što je važno naglasiti je to da svi zadaci i iz prvog i iz drugog dijela
priru
č
nika potje
č
u s razredbenih ispita proteklih godina.
Gradivo je prikazano tako da se njegovom proradom steknu iskustva
koja se ina
č
e stje
č
u na samim razredbenim ispitima. Stoga, na primjer,
zadaci u drugom dijelu priru
č
nika nisu svrstani po nastavnim cjelinama
odnosno podru
č
jima ve
ć
su svrstani onako kako su dolazili na proteklim
ispitima.
Dakle, cilj je pružiti mogu
ć
nost onima koji to žele da što brže i kva-
litetnije ovladaju gradivom iz fizike za op
ć
u gimnaziju te steknu iskustveni
osje
ć
aj kojime smanjuju strah od nepoznatog, tj. od razredbenog ispita.
VAŽNIJE FIZIKALNE KONSTANTE
NAZIV KONSTANTE
SIMBOL VRIJEDNOST KONSTANTE
Brzina svjetlosti u vakuumu
c
2,9979·10
8
ms
-1
≈
3·10
8
ms
-1
Permeobilnost vakuuma
μ
0
4
π
·10
-7
Nm
-1
Permitivnost vakuuma
ε
0
8,854·10
-12
C
2
N
-1
m
-2
Elementarni elektri ni naboj
e
1,602·10
-19
C
Planckova konstanta
h
6,626·10
-34
Js
Gravitacijska konstanta
G
6,67·10
-11
Nm
2
kg
-2
Avogadrov broj
N
A
6,02·10
23
mol
-1
Masa elektrona
m
e
9,11·10
-31
kg
Masa protona
m
p
1,6726·10
-27
kg
Masa neutrona
m
n
1,675·10
-27
kg = 1 u
Plinska konstanta
R
8,314 JK
-1
mol
-1
Rydbergova konstanta
R
1,097·10
7
mol
-1
Faradayeova konstanta
F
9,65·10
4
Cmol
-1
Stefan - Boltzmanova konstanta
σ
5,67·10
-8
Wm
-2
K
-4
Akceleracija sile teže
g
9,80665 ms
-2
≈
9,81ms
-2
Srednji polumjer Zemlje
6,37·10
6
m
Polumjer zemlje na ekvatoru
6,378·10
6
m
Polumjer zemlje na polu
6,357·10
6
m
Masa Zemlje
5,96·10
24
kg
Polumjer Sunca
6,95·10
8
m
Masa Sunca
1,98·10
30
kg
Polumjer Mjeseca
1,74·10
6
m
Masa Mjeseca
7,33·10
22
kg
10
GIBANJA DUŽ PRAVCA
Srednja brzina v u vremenskom intervalu
Δ
t je kvocijent dijela puta
Δ
s , što ga tijelo
prije
đ
e za to vrijeme i vremenskog intervala
Δ
t:
v
s
t
= Δ
Δ
Da bismo dobili trenutnu brzinu u nekoj to
č
ki moramo vremenski interval
Δ
t u
č
initi što je
mogu
ć
e manjim (neizmjerno malenim):
v
v
s
t
t
t
=
=
→
→
lim
lim
Δ
Δ
Δ
Δ
0
0
Jedinica za brzinu je
m
s
ms
=
−
1
.
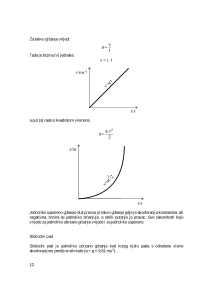
Jednoliko gibanje duž pravca
To je takvo gibanje gdje je na svakom beskrajno malom dijelu puta kvocijent
Δ
s/
Δ
t kon-
stantan, tj. to je takvo gibanje gdje je srednja brzina jednaka trenutnoj duž cijelog puta i
konstantna:
v
v
konst
= =
.
s
t
s
t
v
konst
1
1
2
2
=
= =
.
Brzina je tada jednaka:
v
s
t
=
a put (s) raste linearno s vremenom (t):
s
v t
= ⋅
1
1
Jednoliko ubrzano i jednoliko usporeno gibanje duž pravca
Kad gibanje nije jednoliko, brzina je u svakom trenutku druk
č
ija.
Promijenu brzine odre
đ
ujemo srednjom akceleracijom ( a ).
Srednja akceleracija je omjer razlike brzine
Δ
v u nekom vremenskom intervalu
Δ
t i tog
vremenskog intervala:
a
v
t
v
v
t
t
=
=
−
−
Δ
Δ
2
1
2
1
Jedinica za akceleraciju je (m/s
2
=ms
-2
).
Jednoliko ubrzano gibanje
duž pravca je takvo gibanje pri kojem je kvocijent
Δ
v/
Δ
t
konstantan za svaki
Δ
v i odgovaraju
ć
i
Δ
t, duž cijelog puta, tj. to je takvo gibanje gdje je
akceleracija konstantna, a brzina jednoliko raste s vremenom:
a
a
konst
= =
.
13
To gibanje uzrokuje privla
č
na gravitacijska sila Zemlje.
Brzina kod slobodnog pada iznosi:
v
gs
=
2
a put ili visina s koje tijelo pada je jednaka:
s
v
g
=
2
2
,
s
g t
= ⋅
2
2
Gibanje uz po
č
etnu brzinu
Ako je tijelo imalo po
č
etnu brzinu (v
0
), pa po
č
elo ubrzavati, nakon vremena t njegova
brzina iznosi:
v
v
at
=
+
0
odnosno
v
v
as
2
0
2
2
=
+
Put što
ć
e ga tijelo prije
ć
i u vremenu t tada je jednak:
s
v t
a t
=
+ ⋅
0
2
2
Ako se tijelo gibalo brzinom (v
0
) i po
č
elo usporavati akceleracijom (a), brzina
ć
e nakon
vremena t iznositi:
v
v
a t
=
− ⋅
0
odnosno
v
v
as
2
0
2
2
=
−
a put što
ć
e ga tijelo prije
ć
i u vremenu t tada je jednak:
s
v
t
a t
=
⋅ − ⋅
0
2
2
Nejednoliko gibanje
Gibanje kod kojeg se brzina nepravilno mijenja zove se nejednoliko gibanje.
Funkcionalne veze a-t, v-t i s-t tog gibanja nisu pravilne linije.
14
OSNOVNI ZAKONI GIBANJA
Ako na tijelo ne djeluje nikakva sila ili je rezultanta sila jednaka 0, tijelo miruje ili se giba
jednoliko po pravcu (II Newtnov zakon). Zato kažemo da je tijelo tromo. Mjera tromosti
tijela je masa tijela.
Jedinica za masu u SI je kilogram.
Kada na tijelo dijeluje stalna sila, tijelo se giba jednoliko ubrzano.
Sila koja tijelo ubrzava akceleracijom (a) jednaka je (II Newtnov zakon):
F
m a
= ⋅
Ta sila daje tijelu akceleraciju istog smjera kao i sila, proporcionalnu sili, a obrnuto propor-
cionalnu masi:
a
F
m
=
Jedinica za silu je 1 N (1 njutn):
1
2
N
kgms
=
−
Silu kojom Zemlja privla
č
i sva tijela nazivamo silom težom. Pod djelovanjem sile teže sva
tijela padaju na Zemlju ili pritiš
ć
u na njenu površinu. Akceleracija kojom tijela padaju na
Zemlju naziva se akceleracija slobodnog pada.
Prema II Newtnovom zakonu:
G=m·g
Gdje je G sila teža, m masa tijela i g akceleracija slobodnog pada koja je za sva tijela na
istom mjestu na Zemlji jednaka.
Akceleracija g mijenja se s promijenom zemljopisne širine i nadmorskom visinom. Zato se
i sila teža mijenja promijenom zemljopisne širine i nadmorske visine mjesta na kojem se
tijelo nalazi.
Na 45° zemljopisne širine na morskoj površini g=9,80665 ms
-2
≈
9,81 ms
-2
, što odgovara
našim krajevima.
Težina tijela
(G
t
) je sila kojom tijelo zbog zemljina privlaženja djeluje na horizontalnu
podlogu ili na ovjes. Za slu
č
aj kad tijelo i podloga, odnosno ovjes, miruju ili se gibaju
jednoliko po pravcu s obzirom na Zemlju, težina tijela je po veli
č
ini jednaka sili teži:
G
m g
t
= ⋅
Sila teža i težina su dvije sile razli
č
ite prirode. One djeluju na razli
č
ita tijela. Sila teža
djelu-je na tijelo dok težina djeluje na podlogu na kojoj se tijelo nalazi ili rasteže nit na
kojoj tijelo visi.

16
Za sustav od dva tijela možemo re
ć
i da je zbroj koli
č
ine gibanja obaju tijela prije njihovog
me
đ
usobnog djelovanja jednak zbroju koli
č
ine gibanja tih dvaju tijela nakon njihovog
me
đ
usobnog djelovanja.
Dakle vrijedi:
2
2
1
1
2
2
1
1
v
m
v
m
v
m
v
m
r
r
r
r
′
+
′
=
+
gdje su
2
1
i v
v
r
r
brzine masa m
1
i m
2
prije me
đ
u djelovanja (na pr. sudara) a
2
1
i v
v
′
′
r
r
brzine masa m
1
i m
2
nakon me
đ
usobnog djelovanja.
Kod malih brzina se može uzeti da je masa konstantna, dok kod velikih brzina se masa
mijenja s brzinom. Ovisnost mase o brzini je izražena formulom:
m
m
v
c
=
−
0
2
2
1
gdje je m
0
masa tijela u mirovanju, m masa tijela pri brzini v (relativisti
č
ka masa) a c brzina
svjetlosti.
Drugi Newtonov zakon napisan u obliku:
m
F
a
r
r
=
vrijedi za mnogo manje brzine od brzine svjetlost tj. za slu
č
aj m
≈
m
0
.
Relativisti
č
ki izraz za koli
č
inu gibanja
č
estice mase u mirovanju m
0
i brzine v je:
P
m v
v
c
=
−
0
2
2
1
SLAGANJE I RASTAVLJANJE SILA
Djeluje li na materijalnu to
č
ku više sila (tzv. komponenata) njihovo djelovanje možemo
zamijeniti jednom silom koju zovemo rezultanta:
∑
=
=
+
+
+
=
n
i
i
n
F
F
...
F
F
F
R
1
3
2
1
r
r
r
r
r
r
Kada dvije ili više sila djeluju na istom pravcu u istom smjeru one se mogu zamijeniti
rezultantnom silom koja djeluje u istom pravcu i ima isti smjer, a po veli
č
ini je jednaka
zbroju veli
č
ina svih sila:
2
1
F
F
R
r
r
r
+
=
17
Ako dvije sile djeluju na zajedni
č
kom pravcu u suprotnim smjerovima, veli
č
ina rezultante
je jednaka razlici veli
č
ina komponenata i ima smjer ve
ć
e sile:
2
1
F
F
R
r
r
r
−
=
Kada na tijelo istovremeno djeluju u istoj to
č
ki dvije sile pod kutem, rezultantu dobijemo
konstrukcijom paralelograma tako da na kraj djelovanja prve sile nanosimo smjer i veli
č
inu
druge:
Ako te dvije sile djeluju pod kutem od 90° rezultanta je i opet dijagonala dobijenog pravo-
kutnika (paralelograma), a njen broj
č
ani iznos dobijemo primjenom Pitagorinog teorema za
pravokutni trokut:
R
F
F
=
+
1
2
2
2

19
sin
sin
sin
cos
α
α
α
α
=
=
= ⋅
= ⋅
= ⋅
= ⋅
G
G
h
l
G
G
G
h
l
G
G
G
a
l
1
1
2
Uvjet ravnoteže je da je vektorski zbroj svih sila koje djeluju na materijalnu to
č
ku jednak
nuli:
0
1
2
1
=
=
+
+
∑
=
n
i
i
n
F
F
...
F
F
r
r
r
r
RAD, ENERGIJA, SNAGA
Ako na tijelo djeluje stalna sila u smjeru puta, rad je jednak umnošku sile i prije
đ
enog puta:
W
F S
= ⋅
Ako sila ne djeluje u smjeru puta ve
ć
pod kutem
α
prema putu, tada samo komponenta sile
u smjeru puta vrši rad, te je:
W
F s
F s
s
=
⋅ = ⋅ ⋅
cos
α
20
Ako je 0<
α
<
π
/2 rad je pozitivan, za
α
=
π
/2 rad sile je nula , a za
π
/2<
α
<
π
rad je negativan.
Jedinica za rad je joule (džul):
1 J=1 N·1 m
U F-s grafikonu rad je jednak površini ispod krivulje:
Energija je sposobnost tijela da može vršiti rad i po koli
č
ini je jednaka koli
č
ini rada koje
tijelo može izvršiti.
Jedinica za energiju je ista kao i za rad tj. 1 J.
Tijelo mase m i brzine v ima kineti
č
ku energiju:
E
mv
k
=
2
2
Potencijalnu energiju
imaju tijela koja mogu vršiti rad zbog naro
č
ita položaja. U polju sile
teže tijelo mase m ima potencijalnu energiju:
E
mgh
p
=

22
SLOŽENA GIBANJA
Gibanje tijela je složeno ako tijelo istovremeno vrši dva ili više gibanja.
Pri složenom gibanju vrijedi princip nezavisnosti gibanja koji kaže:
Kad tijelo istodobno vrši dva (ili više) gibanja, giba se tako da se u svakom trenutku nalazi
u to
č
ki do koje bi došlo kad bi najprije izvršilo samo jedno gibanje u odre
đ
enom vremen-
skom razmaku, a zatim neovisno od tog gibanja, drugo gibanje u jednakom vremenskom
razmaku. Složena gibanja mogu biti pravocrtna (hitac prema dolje i vertikalni hitac prema
gore) i krivocrtna (n. pr. horizontalni i kosi hitac). Tijelo koje izvodi gibanje sastavljeno je
od dvaju jednolikih gibanja po pravcu, giba se jednoliko po dijagonali paralelograma:
2
1
2
1
s
s
s
v
v
v
R
R
r
r
r
r
r
r
+
=
+
=
Hitac prema dolje
je složeno gibanje sastavljeno od jednolikog gibanja vertikalno prema
dolje i slobodnog pada. Brzina i put u trenutku t dani su izrazima:
v=v
0
+g·t
s
v t
g
t
=
+
0
2
2
Vertikalni hitac
je složeno gibanje sastavljeno od jednolikog gibanja prema gore brzinom v
0
i slobodnog pada.
Brzina i put u trenutku t dani su izrazima:
v=v
0
-gt
s
v t
g
t
=
−
0
2
2
23
Najve
ć
a visina koju tijelo ispaljeno vertikalno u vis po
č
etnom brzinom v
0
može posti
ć
i
zove se domet (H):
H
v
g
=
0
2
2
Na toj najve
ć
oj visini v=0, a vrijeme potrebno da tijelo postigne tu visinu zove se vrijeme
uspinjanja.
t
v
g
H
=
0
Vrijeme padanja jednako je vremenu uspinjanja; tijelo
ć
e se vratiti brzinom koja je po izno-
su jednaka v
0
ali suprotnog smjera, tj. brzinom -v
0
.
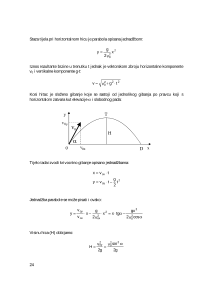
Horizontalni hitac
je složeno gibanje koje se sastoji od jednolikog gibanja u horizontalnom
smjeru i slobodnog pada. Tijelo tada izvodi krivocrtno gibanje:
Put u horizontalnom smjeru:
x
v t
=
0
Put u vertikalnom smjeru:
y
g
t
=
2
2
25
Vrijeme uspinjanja:
t
v
g
v
g
H
oy
=
=
0
sin
α
Domet hica (D):
D
v
v
g
v
g
x
y
=
⋅
=
2
2
0
0
0
sin
α
Vrijeme trajanja hica
t
t
v
g
v
g
H
oy
0
0
2
2
2
=
=
=
sin
α
Svi ovi ra
č
uni vrijede samo uz zanemariv otpor zraka.
JEDNOLIKO GIBANJE PO KRUŽNICI
To je takvo gibanje gdje je brzina konstantna po iznosu, ali stalno mijenja smjer, a oblik
putanje je kružnica:
Obodna ili linearna brzina jednaka je:
v
R
T
=
2
π
gdje je R polumjer kružnice, a T ophodno vrijeme, tj. vrijeme potrebno da tijelo jedanput
obi
đ
e kružnicu.
26
Promjenu smjera brzine uzrokuje centripetalna sila koja ima smjer prema središtu kružnice:
F
mv
R
cp
=
2
ili
F
m
R
T
cp
=
4
2
2
π
a ona tijelu daje centripetalnu akceleraciju:
a
v
R
c
=
2
ili
a
R
T
c
=
4
2
2
π
Umjesto vremena ophoda može se upotrebljavati i podatak koji govori koliko okretaja tijelo
u
č
ini u jedinici vremena. To je frekvencija (f):
f
T
=
1
Vrijeme ophoda (T) se mjeri u sekundama (s) a frekvencija (f) u hertzima (herc) - oznaka
Hz:
1
1
1
Hz
s
s
= =
−
Hertz je frekvencija periodi
č
ne pojeve kojoj period traje 1 s.
INERCIJALNI I AKCELERIRANI SUSTAVI
Osnovni zakoni mehanike vrijede s obzirom na koordinantni sustav koji miruje ili se giba
jednoliko po pravcu. Takvi sustavi u kojima vrijede Newtonovi zakoni zovu se inercijalni
sustavi.

28
gdje je G univerzalna gravitacijska konstanta i ima vrijednost G=6,67·10
-11
m
3
kg
-1
s
-2
, a R
je udaljenost izme
đ
u materijalnih to
č
aka. Taj zakon se još zove Op
ć
i zakon gravitacije
.
Na tijelo koje se nalazi u blizini Zemljine površine djeluje vertikalno prema dolje sila teža
G=m·
g
r
koja je rezultanta gravitacijske i centrifugalne sile zbog vrtnje Zemlje oko svoje
osi. U ve
ć
ini ra
č
una može se zanemariti utjecaj centrifugalne sile i uzeti da je sila teža
jednaka gravitacijskoj sili. Tada je g jednak:
g
G
M
R
ms
Z
Z
= ⋅
≈
−
2
2
9 81
,
Do razli
č
itih vrijednosti veli
č
ine g dolazi zbog spljoštenosti Zemlje i vrtnje oko vlastite osi.
Na polovima je g=9,83 ms
-2
, na ekvatoru g=9,78 ms
-2
, a na 45° zemljopisne širine g=9,81
ms
-2
.
Ako se tijelo mase m nalazi na visini h iznad površine planeta polumjera R i mase M,
gravitacijska sila je tada jadnaka:
F
G
m M
R
h
= ⋅
⋅
+
(
)
2
a akceleracija slobodnog pada:
g
G
M
R
h
h
= ⋅
+
(
)
2
STATIKA KRUTOG TIJELA
Kruto tijelo je takvo tijelo koje pod djelovanjem sila ne mijenja svoj oblik. Hvatište sile se
može mijenjati duž pravca djelovanja sile, a da se pri tome u
č
inak te sile ne promijeni.
Moment
M
r
sile
F
r
s obzirom na os rotacije O (os je okomita na ravninu vrtnje i prolazi
kroz to
č
ku 0)
definiran je izrazom:
29
M=F·d
gdje je d udaljenost pravca djelovanja sile od osi rotacije, tzv. krak sile. Jedinica za moment
sile je Nm.
Kruto tijelo je u ravnoteži ako je vektorski zbroj svih sila i zbroj momenta sile na to tijelo
jednak nuli:
∑
∑
=
=
i
i
i
i
M
F
0
0
r
r
Iz toga proizlazi da je, na primjer, dvostrana poluga:
u ravnoteži kad je F
1
d
1
=F
2
d
2
, a jednostrana poluga:
je u ravnoteži kad je F
3
d
3
=F
4
d
4
.
Ako na slobodno kruto tijelo djeluju dvije sile koje su paralelne i u istom smjeru ali imaju
razli
č
ita hvatišta:
možemo ih zamijeniti njihovom rezultantom koja ima ova svojstva:

31
Veza izme
đ
u obodne (linearne) i kutne brzine:
v
r
= ω
Ako tijelo rotira nejednoliko, uvodi se pojam kutne akceleracije
α
:
α = Δω
Δ
t
Za jednoliko promjenljivu rotaciju vrijede analogni izrazi izrazima za jednoliko
promjenljivo gibanje po pravcu:
a = r
α
gdje je:
α =
=
Δω
Δ
t
konst.
a za opisani kut
ϕ
vrijedi:
ϕ α
ω α
=
= ⋅
2
2
t
t
Ako na tijelo djeluje stalan moment M, koji se još naziva zakretni moment, tijelo
ć
e rotirati
jednoliko ubrzano.
Osnovni zakon rotacije pišemo:
M=
α
·I
ili
α =
M
I
tj. kutna akceleracija rotacije je proporcionalna s momentom sile koja tijelo zakre
ć
e, a obr-
nuto je proporcionalna s momentom tromosti I tijela s obzirom na os rotacije. Moment tro-
mosti I je definiran izrazom:
I
m r
m r
m r
m r
n
n
=
+
+
+ +
1
1
2
2
2
2
3
3
2
2
...
Jedinica za moment tromosti je kgm
2
.
32
Momenti tromosti nekih tijela:
I=mr
2
I
mr
=
1
2
2
moment tromosti materijalne to
č
ke m u udaljenosti r od osi rotacije
moment tromosti kružne plo
č
e polumjera r s obzirom na os koja
prolazi okomito na plo
č
u kroz njeno središte
I
mr
=
2
5
2
I
ml
=
1
12
2
moment tromosti kugle polumjera r s obzirom na os koja prolazi
kroz središte
moment tromosti štapa duljine l s obzirom na os koja prolazi kroz
njegovu sredinu i okomita je na njegovu dužinu
Kineti
č
ka energija tijela koje rotira kutnom brzinom
ω
je:
E
I
k
= ω
2
2
Rad pri konstantnom zakretnom momentu je:
W = M·
ϕ
Snaga pri rotaciji krutog tijela je:
P = M·
ω
HIDROMEHANIKA I AEROMEHANIKA
Tlak je kvocijent sile i površine na koju je ta sila okomito i jednoliko raspore
đ
ena:
p
F
S
=
SI - jedinica za tlak je pascal (1 Pa=1 Nm
-2
).Tlak se još može izraziti jedinicom bar:
1 bar=10
5
Pa
Hidrauli
č
ki tlak
je vanjski tlak i on se prema Pascalovu zakonu širi na sve strane jedna-
ko.To se primjenjuje kod hidrauli
č
ke preše i dizalice:ako na manji klip površine S
1
djeluje-
mo silom F
1
, na drugom kraju preše, na ve
ć
em klipu površine S
2
djelovat
ć
e sila pritiska F
2
:

34
Ona kaže da je zbroj stati
č
kog tlaka p i dinami
č
nog tlaka
ρ
v
2
/2 konstantan. Taj zbroj
zovemo hidrodinami
č
kim tlakom. Taj zakon se može pisati i ovako:
(
)
p
p
V
m v
m v
1
2
2
2
1
2
2
2
−
=
−
tj. rad što ga izvrši razlika tlakova pri gibanju teku
ć
ine utroši se na promjenu kineti
č
ke
energije.
Ako cijev nije horiziontalna Bernoullijeva jednadžba glasi:
p
v
gh
p
v
gh
1
1
2
1
2
2
2
2
2
2
+
+
=
+
+
ρ
ρ
ρ
ρ
gdje su h
1
i h
2
visine promatranih presjeka u odnosu na neki referentni nivo.
Ako idealni fluid istje
č
e iz posude kroz otvor koji se nalazi za visinu h ispod najvišeg nivoa
teku
ć
ine, brzina istjecanja je:
v
gh
=
2
RIJEŠENI PRIMJERI IZ PODRU
Č
JA MEHANIKA
1. Duljina vala helijeve plave spektarne linije iznosi 4,471·10
-4
mm. Izrazi taj podatak u
centimetrima i metrima.
λ
=4,471·10
-4
mm
λ
=? cm
λ
=? m
λ
=4,471·10
-4
mm
λ
=4,471·10
-4
·10
-1
cm
λ
=4,471·10
-5
cm
λ
=4,471·10
-4
mm
λ
=4,471·10
-4
·10
-3
m
λ
=4,471·10
-7
m
2. Koliko je sekundi optere
ć
en most duga
č
ak 80 m ako preko njega prolazi vlak duga
č
ak 80
m brzinom 80 kmh
-1
?
d
1
=80 m
d
2
=80 m
v=80 kmh
-1
=22,22 ms
-1
t=?
t
s
v
d
d
v
m
m
ms
s
= =
+
=
+
=
−
1
2
1
80
80
22 22
7 2
,
,
Most je optere
ć
en od trenutka kad lokomotiva stupi na most pa do trenutka kada ga zadnji
vagon ne napusti pa je s=d
1
+d
2
.
35
3. Automobil je prešao 4/10 puta brzinom 72 km/h, a ostali dio puta brzinom 54 km/h.
Odredi srednju brzinu automobila.
s
1
=4/10 s
v
1
=72 kmh
-1
s
2
=6/10 s
v
2
=54 km/h
-1
v
=?
t
s
v
s
kmh
s
kmh
t
s
v
s
kmh
s
kmh
v
s
t
s
t
t
s
s
kmh
s
kmh
kmh
u
1
1
1
1
1
2
2
2
1
1
1
2
1
1
1
4
10 72
180
6
10 54
2
180
180
2
180
60
=
=
⋅
=
=
=
⋅
=
=
=
+
=
+
=
−
−
−
−
−
−
−
4. Vlak mase 4000 t vozi brzinom 36 km/h. Prije stanice zapo
č
inje jednoliko ko
č
iti. Sila
ko
č
enja je 2·10
5
N. Koliki put prije
đ
e vlak za vrijeme prve minute ko
č
enja?
m=4000 t
v
0
=36 kmh
-1
=10 ms
-1
F=2·10
5
N
t=1 minuta=60 s
s=?
F
m a
a
F
m
N
kg
ms
s
v
t
a t
ms
s
ms
s
m
= ⋅
=
=
⋅
⋅
=
=
⋅ − ⋅
=
⋅
−
⋅
=
−
−
−
2 10
4000 10
0 05
2
10
60
0 05
60
2
510
5
3
2
0
2
1
2
2
,
,
(
)
5. Tramvaj vozi brzinom 18 km/h. Na kojoj udaljenosti ispred semafora mora voza
č
po
č
eti
ko
č
iti ako mu je pri toj brzini za zaustavljanje potrebno 5 s? Pretpostavite da je ko
č
enje
jednoliko.
v
0
=18 km/h=5 ms
-1
v
1
=0
Δ
t=5s
s=?
a
v
v
t
ms
ms
s
ms
s
v t
at
ms
s
ms
s
m
=
−
=
−
= −
=
−
=
⋅ −
⋅
=
−
−
−
−
−
1
0
1
1
2
0
2
1
2
2
0
5
5
1
2
5
5
1
25
2
12 5
Δ
,
6. Automobil se kre
ć
e brzinom 36 km/h. Koliki je put ko
č
enja ako je koeficijent trenja 0,3?
v=36 kmh
-1
=10ms
-1
μ
=0,3
s=?
F
tr
=F
ko
μ
·m·g=m·a
a=
μ
·g=0,3·9,821 ms
-2
=2,943 ms
-2
s
v
a
ms
ms
m
=
=
⋅
=
−
−
2
1 2
2
2
10
2 2 943
16 98
(
)
,
,

37
11. Lift mase 10 t spušta se jednoliko ubrzano u rudnik. Ako je napetost užeta 90 KN,
ubrzanje lifta je:
m=10 t
F
N
=90 KN
a=?
F
N
=G-m·a
F
N
=m·g-m·a
a
mg
F
m
kg
ms
N
kg
ms
N
=
−
=
⋅
⋅
−
⋅
⋅
=
−
−
10 10
9 81
90 10
10 10
0 81
3
2
3
3
2
,
,
12. Predmet mase 0,5 kg jednoliko klizi uslijed trenja niz kosinu s kutom nagiba 30°. Koli-
kom silom treba djelovati na tijelo u smjeru gibanja, da bi se jednoliko uspinjalo istom
brzinom?
m=0,5 kg
α
=30°
F=?
sin
sin
sin
,
,
,
α
α
=
= ⋅
=
⋅
=
⋅
⋅ =
−
F
G
F
G
mg
kg
ms
N
30
0 5
9 81
1
2
2 45
2
o
Da bi se uz trenje tijelo jednoliko uspinjalo ukupna sila je
jednaka 2F:
F
u
=2·F=2·2,45N=4,9N
13.
Č
amac je upravljen prelazio preko rijeke pod kutom od 90° u odnosu na smjer njenog
toka. Brzina
č
amca prema vodi je 5 ms
-1
, a brzina toka rijeke je 2 m/s. Najkra
ć
a udaljenost
me
đ
u obalama jest 200 m. Od jedne do druge obale
č
amac plovi:
α
=90°
v
č
=5 ms
-1
v
r
=2 ms
-1
d=200 m
t=?
v
v
v
m s
m s
ms
v v
s d
s
v d
v
ms
m
ms
m
t
s
v
m
ms
s
r
=
+
=
+
=
=
= ⋅ =
⋅
=
= =
=
−
−
−
−
−
−
2
2
2
2
2
2
1
1
1
1
4
25
29
29
200
5
40 29
40 29
29
40
~
~
~
:
:
14. Njihalo ima nit dugu 1m, a masu 1 kg. Kroz ravnotežni polažaj masa njihala prolazi
brzinom 1 m/s. Napetost niti u tom trenutku je:
38
l=1 m=R
m=1 kg
v=1 ms
-1
F
N
=?
F
G
F
mg
mv
R
kg
ms
kg m s
m
F
N
N
ef
N
= +
=
+
=
⋅
+
⋅
=
−
−
2
2
2
2
1
9 81
1
1
1
10 81
,
,
15. Kamen mase 0,5 kg ispušten s visine od 10 m. Prilikom udara u zemlju kamen je imao
brzinu 12 m/s. Koliki rad je utrošen na savladavanje trenja u zraku? Uzmite g=10 ms
-2
.
m=0,5 kg
h=10 m
v=12 ms
-1
W=?
W
E
J
p
=
−
=
−
=
⋅
⋅
−
⋅
=
−
−
E
mgh
mv
W
kg
ms
m
kg
ms
k
2
2
1 2
2
0 5
10
10
0 5
12
2
14 0
,
,
(
)
,
16. Tijelo mase 1 kg palo je s neke visine za vrijeme od 5 s. Njegova kineti
č
ka energija pri
udaru o tlo iznosila je:
m=1 kg
t=5 s
E
k
=?
v=g·t=9,81 ms
-2
·5 s=49,05 ms
-1
E
mv
kg
ms
J
k
=
=
⋅
=
−
2
1 2
2
1
49 05
2
1202 95
(
,
)
,
17. Kamen je ba
č
en vertikalno uvis na visinu 5 m. Do koje bi visine došao kamen da je bio
izba
č
en dvostrukom po
č
etnom brzinom? Otpor zraka zanemarujemo.
s
1
=5 m
v
2
=2v
0
s
2
=?
s
v
g
s
s
v
g
v
g
v
v
v
v
s
s
m
m
=
=
=
= /
/
=
= ⋅
=
2
2
1
2
2
0
2
2
2
0
2
0
2
0
2
2
1
2
2
2
4
4
4 5
20
18. Dizalo se penje ubrzanjem 2 ms
-2
. Na podu kabine dizala nalazi se teret mase 10 kg.
Kolikom silom pritiš
ć
e teret na pod kabine?
a=2 ms
-2
m=10 kg
F
p
=?
F
p
=G+ma=mg+ma=m(g+a)=10kg (9,81ms
-2
+2ms
-2
) =118,1 N
19. Žlijeb je savijen u obliku kruga polumjera 1 m i leži u vertikalnoj ravnini. Kojom
minimalnom brzinom treba gurnuti sitno tijelo iz položaja ravnoteže da bi napravilo puni
krug? (Trenje tijela o žlijeb zanemarite, za ubrzanje sile teže uzmite 9,81 ms
-2
)

40
23. Tijelo mase 0,5 kg i gusto
ć
e 4·10
3
kgm
-3
visi na koncu tako da je uronjeno u teku
ć
inu
gusto
ć
e 1,5·10
3
kgm
-3
. Napetost niti iznosi?
m=0,5 kg
ρ
=4·10
3
kgm
-3
ρ
t.
=1,5·10
3
kgm
-3
F
N
=?
F
G
F
m g
V
g
m g
m
g
F
m g
g
F
kg
ms
kgm
kgm
ms
F
N
N
u
tij
t
tij
t
N
t
tij
N
N
= −
= ⋅ −
⋅ ⋅ = ⋅ −
⋅ ⋅
=
−
⋅
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
=
−
⋅
⋅
⋅
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
=
−
−
−
−
ρ
ρ
ρ
ρ
ρ
0 5
9 81
1 5 10
4 10
9 81
3 07
2
3
3
3
3
2
,
,
,
,
,
24. Kota
č
koji se vrti s 480 okretaja u minuti po
č
inje se zaustavljati jednoliko usporeno.
Koliki je ukupni broj okretaja kota
č
a ako se zaustavi u vremenu od 0,5 minuta?
ν
=480 min
-1
Δ
t=0,5 min
N=?
N
t
t
t
=
=
= ⋅ = ⋅ =
⋅
=
−
ρ
π
α
π
ω
π
ν
2
4
4
2
480
0 5
2
120
2
1
min
, min
25. Širim djelom vodoravno položene cijevi struji voda brzinom 4 m/s. Razlika tlakova ši-
reg i suženog dijela cijevi iznosi 8·10
3
Pa, te brzina proljevanja u užem dijelu cijevi iznosi:
v
1
=4 ms
-1
p
1
-p
2
=8·10
3
Pa
v
2
=?
Iz Bernoullijeve jednadžbe proizlazi:
p
v
p
v
v
p
p
v
v
p
p
v
kgm
Pa
m s
v
m s
ms
1
1
2
2
2
2
2
2
1
2
1
2
2
1
2
1
2
3
3
3
2
2
2
2
2
1
2
2
2
2
2
2
10
8 10
16
32
5 65
+
=
+
=
−
+
=
−
+
=
⋅ ⋅
+
=
=
−
−
−
−
ρ
ρ
ρ
ρ
ρ
(
)
,
26. Sa stupa visokog 20 m izba
č
en je horizontalno kamen po
č
etnom brzinom 10 m/s. u
kojoj
ć
e udaljenosti od stupa pasti na zemlju
h=20 m
v
0
=10 ms
-1
x=?
h
g
t
t
h
g
x
v
t
v
h
g
ms
m
ms
m
=
⇒
=
=
⋅ =
⋅
=
⋅
⋅
=
−
−
2
2
2
10
2 20
9 81
20 2
2
0
0
1
2
,
,
41
27. Kolikom brzinom izlazi mlaz vode iz otvora cijevi ako se taj mlaz penje vertikalno do
visine 4,1 m. Zanemarite gubitak zbog trenja?
h=4,1 m
v=?
Sva kineti
č
ka energija mlaza se pretvorila u potencijalnu.
mv
mgh
v
gh
ms
m
ms
2
2
1
2
2
2 9 81
4 1
8 968
=
=
=
⋅
⋅
=
−
−
,
,
,

43
gdje je x - elongacija, a k tzv. konstanta opruge odnosno konstanta opiranja izražava se u
Nm
-1
. Sila je proporcionalna elongaciji, ali je suprotnog smijera.
Izraz za period titranja je:
T
m
k
=
2
π
Titranje sjene materijalne to
č
ke koja se giba jednoliko po kružnici
Kad se materijalna to
č
ka giba jednoliko po kružnici, njena sjena titra harmoni
č
ki. Pri tome
je kutna brzina to
č
ke jednaka kružnoj frekvenciji titranja, a ophodno vrijeme to
č
ke jednako
je periodu titranja projekcije te to
č
ke.
Jednadžba harmoni
č
kog titranja je:
x
A
T
t
A
t
=
⋅ +
⎛
⎝⎜
⎞
⎠⎟
=
⋅ +
sin
sin(
)
2
0
0
π
ϕ
ω
ϕ
gdje je:
x - elongacija
A - amplituda (maksimalna elongacija)
ω
t+
ϕ
0
- faza titranja u trenutku t
ϕ
0
- faza titranja u trenutku t=0
Brzina to
č
ke koja harmoni
č
ki titra je:
v
k
m
A
x
f A
x
=
−
=
−
(
)
2
2
2
2
2
π
Akceleracija to
č
ke koja harmoni
č
ki titra je:
a
T
x
f x
= −
⋅ = −
4
4
2
2
2
2
π
π
44
Period harmoni
č
kog titranja je jednak:
T
m
k
mx
F
=
=
2
2
π
π
Matemati
č
ko njihalo
Matemati
č
ko njihalo se sastoji od to
č
kaste mase obješene na nerastezljivu nit zanemarive
mase. Za male amplitude to njihalo titra periodi
č
ki s periodom:
T
l
g
=
2
π
gdje je l duljina njihala, a g akceleracija slobodnog pada.
MEHANI
Č
KI VALOVI
Val je širenje titraja iz izvora vala kroz neko sredstvo. Kad se energija titranja prenosi
okomito na smjer širenja valova govorimo o transverzalnim valovima, a kad se energija
titranja prenosi u pravcu širenja vala govorimo o longitudinalnim valovima.
Valna duljina (
λ
) je udaljenost izme
đ
u dviju najbližih to
č
aka vala koje titraju u istoj fazi, tj.
to je udaljenost za koju se val proširio dok
č
estica u izvoru napravi jedan puni titraj:
λ = ⋅ =
v T
v
f
Jednadžba vala govori o elongaciji to
č
ke koja je udaljena za x od izvora vala, ako se val
giba brzinom v i pozitivnom smjeru osi x:
y x t
A
t
T
x
( , )
sin
=
⋅ − ⋅
⎛
⎝⎜
⎞
⎠⎟
2
2
π
π
λ
gdje je A amplituda vala, a
2
π
λ
⋅
x
zaostatak u fazi neke to
č
ke na udaljenosti x od izvora
vala.
Razlika u fazi (
Δϕ
) dviju
č
estica koje titraju na udaljenostima x
1
i x
2
od izvora vala dana je
izrazom:
Δϕ =
−
2
1
2
π
λ
x
x

46
Brzina zvuka u
č
vrstim tijelima je:
v
E
=
ρ
gdje je E Youngov modul elasti
č
nosti, a
ρ
gusto
ć
a sredstva.
Dopplerov efekt
Ako se neki izvor valova i opaža
č
me
đ
usobno približavaju
č
ini se da se frekvencija izvora
pove
ć
ava odnosno smanjuje kad se izvor i opaža
č
me
đ
usobno udaljuju. To je Dopplerov
efekt.
Kod valova zvuka mijenja se i visina tona koji opaža
č
č
uje. Visina tona ovisi o broju valnih
duljina koje u 1 sekundi dopru do našeg uha.
Ako je
ν
prava frekvencija izvora,
ν
' frekvencija koju prima uho, v
z
brzina zvuka, a v brzi-
na tijela koje se giba mogu
ć
a su dva slu
č
aja:
a) opaža
č
se giba prema mirnom izvoru zvuka i tada je frekvencija:
′ =
±
⎛
⎝
⎜
⎞
⎠
⎟
ν
ν
1
v
v
z
gdje pozitivni predznak ozna
č
ava približavanje, a negativni udaljavanje od izvora
b) izvor zvuka se giba u odnosu prema mirnom opaža
č
u i tada je frekvencija:
′ = ⋅
ν
ν
1
1 m
v
v
z
I ovdje pozitivni i negativni predznak ozna
č
uju približavanje odnosno udaljavanje od
opaža
č
a.
47
RIJEŠENI PRIMJERI IZ PODRU
Č
JA HARMONI
Č
KO TITRANJE I
VALOVI
1. Period titranja matemati
č
kog njihala je 3,6 s. Odredite vrijeme potrebno da se njihalo od
ravnotežnog položaja udalji za pola amplitude.
T=3,6 s
x=A/2
t=?
x
A
t
A
A
t
T
t
T
t
T
T
t
T
s
s
=
=
⋅
⋅ =
⋅ =
=
=
=
sin
sin
sin
,
,
ω
π
π
π
2
2
2
1
2
2
6
12
3 6
12
0 3
2. Na oprugu konstante elasti
č
nosti 10 Nm
-1
, koja slobodno visi objesimo uteg mase 0,1 kg.
Kolika
ć
e biti maksimalna brzina utega?
k=10 Nm
-1
m=0,1 kg
v
max
=?
G
k x
x
G
k
m g
k
A
maksima
a elongacija
v
A
T
ako je
T
m
k
v
A
m
k
A
m
k
m g
k
m
k
kg
ms
Nm
kg
Nm
v
ms
= − ⋅
=
=
⋅ = −
=
⋅
=
⇒
=
⋅
=
=
⋅ =
⋅
=
−
−
−
−
ln
,
,
,
,
2
2
2
2
0 1
9 81
10
0 1
10
0 981
2
1
1
1
π
π
π
π
3. Duljina sekundnog njihala (tj. onog s poluperiodom 1s) iznosi na ekvatoru (g=9,72 ms
-2
):
T/2=1 s
g=9,72 ms
-2
l=?
T
l
g
l
T
g
s
ms
m
=
=
⋅ =
⋅
⋅
=
−
2
4
2
9 72
4 3 14
0 985
2
2
2
2
2
π
π
(
)
,
,
,

49
TOPLINA
MOLEKULSKI SUSTAV TVARI
Sva tijela u prirodi se sastoje od atoma i molekula. Atomi su najsitnije
č
estice neke tvari
koje se kemijskim reakcijama ne mogu pojednostavniti. Molekule su skupine kemijski
vezanih atoma, a imaju ista kemijska svojstva kao i sama tvar koju
č
ine. Veli
č
ina atoma ili
molekule je reda veli
č
ine 10
-9
m, a masa reda veli
č
ine 10
-27
kg. Osim kg za izražavanje
mase atoma i molekula
č
esto upotrebljavamo unificirane atomsku jedinicu mase (u):
1 u=1,66·10
-27
kg
a to je
1
12
mase atoma ugljika
6
12
C
.
Relativna atomska masa (A
r
) je broj koji pokazuje koliko je puta masa nekog atoma ve
ć
a
od atomske jedinice mase. Jednako tako relativna molekulska masa (Mr) pokazuje koliko je
puta masa neke molekule ve
ć
a od unificirane atomske jedinice mase.
Koli
č
ina tvari se izražava jedinicom koju se naziva mol. Jedan mol je koli
č
ina tvari sustava
koji sadrži toliko osnovnih
č
estica koliko ima atoma 0,012 kg ugljika izotopa
6
12
C .
Molarna masa (M) je masa jednog mola neke tvari:
M
m
n
=
gdje je M molarna masa, m masa tvari, a n broj molova.
Broj jedinki u jednom molu zove se Avogadrov broj:
N
mol
A
=
⋅
−
6 023 10
23
1
,
Jedan mol bilo koje tvari sadrži isti broj jedinki (molekula, atoma, iona).
Volumen 1 mola bilo kojeg plina pri normiranim uvijetima (273 K, 101 325 Pa) jednak je
2,24·10
-2
m
3
.
Jednaki volumeni razli
č
itih plinova izmjereni pri jednakom tlaku i temperaturi sadrže isti
broj molekula (Avogadrov zakon).
Kada na
č
vrsto tijelo djeluje sila mijenja se položaj njegovih molekula, a time i oblik tijela.
Za najjednostavniju deformaciju tog tijela - istezanje vrijedi Hookeov zakon:
ε = ⋅
1
E
P
gdje je E Youngov modul elesti
č
nosti,
ε
=
Δ
l/l relativno produljenje, a p=F/S sila na jedinici
presjeka ili napetost.
50
Sile me
đ
u molekulama uzrokuju napetost površine i kapilarnost. Koeficijent napetosti
površine
σ
je dan izrazom:
σ = Δ
Δ
W
S
gdje je
Δ
W izvršen rad pri pove
ć
anju površine
Δ
S.
Koeficijent površinske napetosti
σ
je jednak i omjeru sile i duljine na koju ta sila okomito
djeluje:
σ =
F
l
2
PROMJENA UNUTRAŠNJE ENERGIJE
Unutrašnja energija tijela je zbroj kineti
č
ke energije gibanja svih molekula tijela i potenci-
jalne energije njihova me
đ
udjelovanja.
Temperaturtra (T) je mjera za srednju kineti
č
ku energiju toplinskog gibanja molekula i što
je kineti
č
ka energija ve
ć
a, to je temperatura ve
ć
a. Jedinica za temperaturu je kelvin (K).
Veza izme
đ
u apsolutne temperature T izražene Kelvinima i temperature t izražene u Celzi-
jusovim stupnjevima je:
T
K
t
C
=
+
273 15
,
o
Unutarnju energiju tijela ili sustava tijela možemo promijeniti na dva na
č
ina, me
đ
usobnim
dodirom dvaju tijela razli
č
itih temperatura i mehani
č
kim radom:
Δ
U=Q+W
gdje je
Δ
U promjena unutrašnje energije, Q toplina, a W mehani
č
ki rad.
Rad W može biti pozitivan ili negativan, ovisno o tome vršimo li rad nad tijelom ili tijelo
vrši rad.
Ako se unutrašnja energija tijela mijenja samo zato što su u dodiru dva tijela razli
č
itih
temperatura (W=0) onda je W=Q.
Toplina
Q je dio unutrašnje energije tijela koja prolazi s jednog tijela na drugo zbog razlike
temperatura tih tijela. Toplina i unutrašnja energija se mjere džulima (J).
Pri zagrijavanju i hla
đ
enju primljena odnosno predana koli
č
ina topline je:
Q=mc
Δ
T
gdje je c specifi
č
ni toplinski kapacitet, m masa tijela a
Δ
T=T
2
-T
1
promjena temperature.

52
Toplina isparavanja
je koli
č
ina topline koja se troši (ili osloba
đ
a) pri isparavanju odnosno
kondenzaciji:
Q=m·r
gdje je m masa tijela, a r specifi
č
na toplina isparavanja.
Toplina izgaranja
je koli
č
ina topline koja se osloba
đ
a pri potpunom izgaranju goriva mase
m i specifi
č
ne topline izgaranja q:
Q=m·q
Korisnost grija
č
a (toplinskog stroja) je dana omjerom iskorištene topline Q
k
i ukupno
ulpžene topline Q
u
:
η =
⋅
Q
Q
k
u
100%
TOPLINSKO RASTEZANJE
Č
VRSTIH TVARI I TEKU
Ć
INA
Č
vrste tvari se zagrijavanjem rastežu, a hla
đ
enjem stežu. Koeficijent linearnog rastezanja
β
je definiran:
β =
−
⋅
l
l
l
t
t
0
0
gdje je l
0
duljina tijela (štapa, cijevi) pri 0 °C, l
t
duljina tijela na t °C.
Jedinica za koeficijent linearnog rastezanja je K
-1
.
Duljina tijela nakon zagrijavanja l
t
je:
l
t
=l
0
(1+
β
t)
Kad su kod
č
vrstog tijela sve dimenzije podjednako izražene govorimo o kubnom rasteza-
nju.
Neka tijelo kod 0 °C ima volumen V. Povisimo li tijelu temperaturu za t (od 0 °C do t °C)
njegov
ć
e se volumen pove
ć
ati za:
Δ
V=
α
t·V
0
α
- je koeficijent volumnog (kubnog) rastezanja:
α
β
=
−
⋅
≈
V
V
V
t
t
0
0
3
53
Kod temperature t tijelo
ć
e prema tome imati volumen:
V
t
=V
0
(1+
α
t)
Ovaj izraz vrijedi i za teku
ć
ine i za šuplja
č
vrsta tijela.
Gusto
ć
a tijela na temperaturi t iznosi:
ρ
ρ
α
t
t
=
+ ⋅
0
1
PROMJENA STANJA PLINA
Model idealnog plina predpostavlja da su molekule plina materijalne to
č
ke koje nemaju
volumena i me
đ
u kojima nema me
đ
umolekularnih sila. Fizi
č
ko stanje takvog idealnog
plina je opisano trima veli
č
inama: volumenom (V), tlakom (p) i temperaturom (T). Mijenja
li se jedna od tih triju veli
č
ina, promijenit
ć
e se bar jedna od preostale dvije.
Tlak plina uzrokuju sudari molekula plina na stijenkama posude, pa taj tlak ovisi o broju
molekula u jedinici volumena i o njihovoj kineti
č
koj energiji:
P
N
V
m v
N
V
E
m
k
=
=
2
3
2
2
3
2
gdje je N broj molekula u volumenu V, m
m
masa molekule plina i v
2
srednja vrijednost
kvadrata brzine molekula.
Apsolutna temperatura T povezana je s gibanjem molekula plina relacijom:
T
N
nR
E
N
R
E
k
A
k
2
3
2
3
=
gdje je R plinska konstanta, n broj molova plina, a N
A
Avogadrov broj.
Izotermna promjena stanja plina
je takova promjena kod koje temperatura ostaje stalna, a
promjenu tlaka i volumena opisuje Boyle - Mariotteov zakon:
t=konst.
p
1
V
1
=p
2
V
2
=konst.
Kod konstantne temperature uz porast tlaka, volumen plina pada i obrnuto.

55
Jednadžba stanja plina
Povezanost sva tri parametra koji opisuju stanje plina (volumen, tlak i temperatura) može-
mo izraziti zakonom u kojem su sadržana sva tri plinska zakona. To je jednadžba stanja
plina:
p V
T
p V
T
1
1
1
2
2
2
=
ili kra
ć
e:
p V
T
konst
⋅ =
.
Promatra li se koli
č
ina plina od 1 mol,
č
iji je volumen V
m
dobija se:
p V
T
p V
T
m
m
⋅
=
0
0
0
p
0
= 101 325 Pa
V
om
= 2,24·10
-2
m
3
T
0
= 273,15 k
p V
T
R
JK
mol
m
0
0
0
1
1
8 314
= =
−
−
,
Jednadžba tada poprima oblik:
p·V
m
=RT
Ako promatramo koli
č
inu od n molova plina jednadžba glasi:
p·V=nRT
Promatramo li smjesu od nekoliko plinova, ukupni
ć
e tlak biti jednak zbroju parcijalnih
tlakova pomiješanih plinova.
Tlak smjese je:
p=p
1
+p
2
+p
3
+...
gdje su p
1
, p
2
, p
3
tlakovi pojedinih plinova.
Parcijalni tlak plina je tlak što bi ga imala jedna od pomiješanih koli
č
ina plina kad bi sama
ispunila
č
itav prostor u kojem se nalazi smjesa.
56
MEHANI
Č
KI RAD I UNUTRAŠNJA ENERGIJA
Unutrašnja energija sustava se može promijeniti dovo
đ
enjem (odvo
đ
enjem) topline kao i
obavljanjem rada. Prema prvom zakonu termodinamike je:
Δ
U=Q+W
gdje je
Δ
U promjena unutrašnje energije, Q dovedena (odvedena) koli
č
ina topline, a W
obavljeni rad.
Plin pri širenju obavlja rad. Taj rad ovisi o vrsti procesa kojim se plin rasteže. Pri izobar-
nom širenju (p=konst.) pri tlaku p od volumena V
1
do volumena V
2
rad je jednak:
W=p(V
2
-V
1
)
Pri izohornom procesu (V=konst.) plin se ne širi, te je i rad nula.
Pri adijabatskom procesu (Q=0, nema izmjene topline s okolinom) pa se rad obavlja na
ra
č
un smanjenja unutrašnje energije.
W=-
Δ
U
Pri izotermnom procesu (T=konst.) nema promijene unutrašnje energije (
Δ
U=0) te se sva
dovedena toplina pretvara u rad W=Q.
U p-V dijagramu rad je jednak površini ispod krivulje. Korisnost idealnog toplinskog stroja
(Carnotova) je:
η =
=
−
=
−
W
Q
Q
Q
Q
T
T
T
2
2
1
2
2
1
2
gdje je Q
2
dovedena toplina, Q
1
toplina predana hladnijem spremniku, T
2
temperatura topli-
jeg, a T
1
temperatura hladnijeg spremnika.
Kod toplinskih strojeva dio unutrašnje energije plinova ili para (radnog tijela) se pretvara u
rad. To je mogu
ć
e samo ako postoji razlika temperatura spremnika izme
đ
u kojih kruži
radno tijelo.
Za vrijeme jednog kružnog procesa radno tijelo primi od toplijeg spremnika toplinu Q
2
i
preda hladnijem spremniku toplinu Q
1
. Promjena topline Q
2
-Q
1
je rad što ga je radno tijelo
izvršilo.
Korisnost
η
nekog toplinskog stroja govori o tome koliki je dio topline dobivene od topli-
jeg spremnika prešao u mehani
č
ki rad.

58
6. U automobilskoj gumi nalazi se zrak pod tlakom 6·10
5
Pa kod 293 K. Dok se auto giba,
temperatura u gumi poraste na 308 K. Za koliko se pove
ć
a tlak plina u gumi, ako je volu-
men zraka konstantan?
p=6·10
5
Pa
T
1
=293 K
T
2
=308 K
Δ
p=?
Δ
Δ
p
p
p
p
T
T
p
Pa
K
K
Pa
p
Pa
Pa
Pa
=
−
=
⋅
−
= ⋅
⋅
− ⋅
=
− ⋅
=
⋅
=
⋅
2
1
1
1
2
1
5
5
5
5
4
6 10
308
293
6 10
6 307
6 10
0 307 10
3 07 10
( ,
)
,
,
7. U zatvorenoj posudi volumena 10 l nalazi se 0,5 mola vodika. Koliki
ć
e biti izvršeni rad
ako ga zagrijemo od 0°C do 100°C?
V=10 l=10·10
-3
m
3
n==0,5 mol
t
1
=0°C
t
2
=100°C
W=?
W=p
Δ
V=0
jer nema promijene volumena.
8. Posudu koja sadrži 5 litara zraka pri normalnom tlaku sjedinimo s potpuno praznom
(vakuum) posudom 4,5 litara. Koliki je kona
č
ni tlak zraka, ako je proces izoterman
(T=konst.)?
p
1
=101 325 Pa
V
1
=5 l=5·10
-3
m
3
V
2
=(5+4,5) l=9,5·10
-3
m
3
p
2
=?
p V
p V
p
p V
V
Pa
m
m
Pa
1
1
2
2
2
1
1
2
3
3
3
3
101325
5 10
9 5 10
53329
=
=
=
⋅ ⋅
⋅
=
−
−
,
9. Elektri
č
nim ronilom snage 1 Kw zagrijavamo tri minute vodu mase 2 kg. Za koliko
ć
e se
pri tom povisiti temperatura vode ako nema toplinskih gubitaka? Specifi
č
ni toplinski kapa-
citet vode iznosi 4190 Jkg
-1
K
-1
.
P=1 kW=10
3
W
t=3 min=180 s
m=2 kg
Δ
T=?
W
Q
P t
mc T
T
p t
mc
W
s
kg
Jkg
K
K
=
⋅ =
= ⋅ =
⋅
⋅
=
−
−
Δ
Δ
10
180
2
4190
21 47
3
1
1
,
10. U aluminijskoj plo
č
i napravljen je kružni otvor polumjera 2,5 cm na temperaturi 20°C.
Koliko
ć
e iznositi polumjer otvora na temperaturi 200°C? Koeficijent linearnog rastezanja
aluminija je 24·10
-6
K
-1
.
l
t
=2,5 cm
t=20°C=293 K
t
2
=200°C=473 K
l
2
=?
l
l
t
l
l
t
t
t
=
+
=
+
0
0
1
1
(
)
α
α
59
l
l
t
l
t
t
l
cm
K
K
K
cm
t
2
0
2
2
2
6
1
6
1
1
1
2 5
1 24 10
293
1 24 10
473
2 51
=
+
=
+
+
=
+
⋅
⋅
⋅ +
⋅
⋅
=
−
−
−
(
)
(
)
,
(
)
,
α
α
α
11. Nakon koliko
ć
e vremena iz kalorimetra ispariti 100 g vode ako je u kalorimetar uro-
njen grija
č
snage 1000 W? Po
č
etna masa vode u kalorimetru bila je 2000 g, a njena tempe-
ratura iznosila 20°C. (Specifi
č
ni toplinski kapacitet vode je 4190 Jkg
-1
K
-1
, a specifi
č
na
toplina isparavanja vode je 2,26·10
6
Jkg
-1
.)
m=100 g=0,1 kg
P=1000 W
m
1
=2000 g=2 kg
t
1
=20°C
c=4190 Jkg
-1
K
-1
r=2,26·10
6
Jkg
-1
t
2
=100°C
t=?
Grija
č
mora prvo zagrijati svu vodu do vrenja, a tek
onda
ć
e nastupiti isapravanje.
W
Q
Q
P t
m c t
mr
t
m c T
mr
P
t
kg
Jkg
K
K
kg
Jkg
W
t
s
s
r
= +
⋅ =
+
=
+
=
⋅
⋅
+
⋅
⋅
=
+
=
−
−
−
1
1
1
1
6
1
2
4190
80
0 1
2 26 10
1000
670400
226000
1000
896 4
Δ
Δ
,
,
,

61
Jakost polja broj
č
ano je jednaka sili koja djeluje na jedini
č
ni pozitivan naboj, a smjer
vektora
E
r
je isti kao i smjer sile
F
r
.
Jedinica za jakost el. polja je N/C, odnosno ekvivalentna jedinica V/m.
Jakost elektri
č
nog polja to
č
kastog naboja Q na udaljenosti r od naboja je:
E
Q
r
r
=
⋅
1
4
0
2
πε ε
Izraz vrijedi i za jakost polja nabijene kugle jer je jakost polja kugle upravo tolika kao da je
sav naboj koncentriran u središtu kugle. Udaljenost r je tada razmak od središta kugle do
to
č
ke u kojoj promatramo jakost polja.
Potencijal neke to
č
ke elektri
č
nog polja je jednak radu potrebnom za pomicanje jedini
č
nog
pozitivnog naboja iz te to
č
ke u referentnu to
č
ku nultog potencijala:
ϕ =
W
Q
Jedinica za potencijal je volt:
1V=
1
1
J
C
Veli
č
ina potencijalne energije odre
đ
ene to
č
ke polja dana je izrazom:
E
W
Q
p
=
= ⋅ϕ
Potencijal to
č
kastog naboja Q ili nabijene kugle u to
č
ki na udaljenosti r od naboja ili sredi-
šta kugle je:
ϕ
πε ε
=
⋅
1
4
0
r
Q
r
Potencijal to
č
aka na površini nabijene kugle polumjera R je jednak:
ϕ
πε ε
=
⋅
1
4
0
r
Q
R
Razlika potencijala (
ϕ
1
-
ϕ
2
)se naziva napon:
U
W
Q
=
−
=
ϕ
ϕ
1
2
62
Napon izme
đ
u dvije to
č
ke je jednak radu što ga treba izvršiti pri prenošenju naboja Q iz
jedne to
č
ke u drugu. Jedinica za napon je ista kao i za potencijale 1 Volt (1V). Iz izraza
W=Q·U izvodi se još jedna jedinica za energiju, 1 eV (elekron volt).
1eV je energija koju dobije elektron (ili neka druga
č
estica s nabojem e) kad prije
đ
e razliku
potencijala od 1V.
1eV=1,6·10
-19
C·1 V=1,6·10
-19
J
1KeV=1000eV=1,6·10
-16
J
1MeV=10
6
eV=1,6·10
-13
J
U homogenom elektri
č
nom polju jakosti E, kod naboja Q prelazi udaljenost d obavlja se
rad jednak:
W=F·d=Q·E·d=Q·u
odakle je:
E
U
d
=
pa tako i jedinica za jakost elektri
č
nog polja (
1
1
V
m
).
ELEKTRI
Č
NI KAPACITET I KONDENZATORI
Elektri
č
ni kapacitet vodi
č
a je jednak omjeru naboja Q koji se nalazi na vodi
č
u i potencijala
ϕ
:
C
Q
=
ϕ
Jedinica za kapacitet je farad (F):
1
1
1
F
C
V
=
Kondenzator se sastoji od dvaju vodi
č
a izme
đ
u kojih je izolator (dielektrik). Kapacitet
kondenzatora je omjer naboja na kondenzatoru i napona izme
đ
u plo
č
a kondenzatora:
C
Q
Q
U
=
−
=
ϕ
ϕ
1
2

64
Energija pohranjena u nabijenom kondenzatoru je jednaka:
W
Q U
C U
= ⋅ ⋅ = ⋅ ⋅
1
2
1
2
2
OHMOV ZAKON I ZAKON ELEKTRI
Č
NOG OTPORA
Elektri
č
na struja je svako usmjereno gibanje elektri
č
nog naboja. Jakost struje I je definirana
kao ona koli
č
ina naboja
Δ
Q koja u vremenu
Δ
t pro
đ
e presjekom vodi
č
a:
I
Q
t
= Δ
Δ
Ako je struja konstantna, onda vrijedi:
I
Q
t
=
Jedinica za jakost el. struje je amper (A).
Gusto
ć
a struje je jakost struje po jedinici presjeka vodi
č
a:
j
I
S
=
a jedinica za mjerenje gusto
ć
e struje je Am
-2
.
Pod djelovanjem elektri
č
ne sile
E
e
F
r
r
−
=
slobodni elektroni u metalima dobivaju prirast
brzine u smjeru el. sile:
v
E
= ⋅
μ
gdje je
μ
pokretljivost elektrona koja se mjeri u m
2
s
-1
V
-1
.
65
Za metalni vodi
č
duljine l i površine presjeka S Ohmov zakon glasi:
I
Q
t
n e S v
t
t
n e S v
n e
S
l
U
G U
=
= ⋅ ⋅ ⋅ ⋅
= ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ = ⋅
Δ
Δ
Δ
Δ
μ
n je broj elektrona u jedinici volumena, e elementarni naboj,
μ
pokretljivost slobodnih
elektrona, U napon na krajevima vodi
č
a, G vodljivost.
Elektri
č
na vodljivost G se mjeri u siemensima (1
1
1
S
A
V
=
).
Recipro
č
na vrijednost elektri
č
ne vodljivosti je elektri
č
ni otpor (R):
R
G
n e
l
S
=
=
⋅ ⋅
⋅
1
1
μ
Jedinica za mjerenje otpora je je ohm(1
1
1
Ω =
V
A
)
Ohmov zakon
napisan pomo
ć
u otpora za dio strujnog kruga je:
I
U
R
=
gdje je I jakost struje što te
ć
e vodi
č
em, U napon na krajevima vodi
č
a a R otpor vodi
č
a.
Zakon elektri
č
nog otpora
Elektri
č
ni otpor R vodi
č
a duljine l i presjeka S jednak je:
R
n e
l
S
l
S
=
⋅ ⋅
⋅ = ⋅
1
μ
ρ
gdje je:
ρ
μ
=
⋅ ⋅
1
n e
elektri
č
na otpornost materijala koja se mjeri u
Ω
m.
Elektri
č
ni otpor vodi
č
a raste s el. otpornoš
ć
u materijala i duljinom vodi
č
a, a pada s površi-
nom presjeka vodi
č
a.
Elektri
č
ni otpor vodi
č
a mijenja se i s temperaturom prema zakonu:
R
R
t
t
=
+
0
1
(
)
α
gdje je R
0
otpor kod 0°C, R
t
otpor kod temperature t, i
α
temperaturni koeficijent otpora.

67
Serijski spoj otpora
. Ukupni otpor serijski spojenih otpora jednak je zbroju pojedinih
otpora:
R=R
1
+R
2
+R
3
+...
Pri serijskom spajanju otpora kroz sve otpore te
č
e ista jakost struje, pa je ukupni napon
jednak sumi padova napona na pojedinim vodi
č
ima:
U=U
1
+U
2
+U
3
=IR
1
+IR
2
+IR
3
Paralelni spoj otpora
. Pad napona na krajevima svih vodi
č
a spojenih u paralelu je jednak:
U=I
1
R
1
=I
2
R
2
=I
3
R
3
Ukupni otpor paralelno spojenih vodi
č
a je:
1
1
1
1
1
2
3
R
R
R
R
=
+
+
Jakost struje I koja je došla u to
č
ku grananja jednaka je sumi jakosti struja koje su iz to
č
ke
grananja izašle:
I=I
1
+I
2
+I
3
68
Serijsko spajanje izvora
. Pri serijskom spajanju izvora ukupna elektromotorna sila
ε
jdnaka
je zbroju elektromotornih sila
ε
i
pojedinih izvora. Jednako je i unutrašnji otpor jednak
zbroju pojedinih unutrašnjih otpora pa Ohmov zakon u tom slu
č
aju glasi:
I
R
R
i
i
n
n
i
n
i
=
∑
+
∑
=
=
ε
1
1
Paralelni spoj izvora
. Kod paralelnog spajanja više izvora jednake elektromotorne sile,
ukupna elektromotorna sila jednaka je elektromotornoj sili pojedinog izvora, a ukupni se
unutrašnji otpor smanjuje jer su paralelno spojeni.
Ohmov zakon ima slijede
ć
i oblik:
I
R
R
n
u
=
+
ε
RAD I SNAGA ELEKTRI
Č
NE STRUJE
Rad što ga izvrši struja jakosti I za vrijeme t, ako je na krajevima vodi
č
a napon U jednak je:
W=U·I·t
Snaga struje je:
P=U·I
Jedinica za rad je joule (J), a jedinica za snagu watt (W).
Za izražavanje rada upotrebljava se još i 1 kWh:
1kWh=10
3
W·3600 s=3,6·10
6
J
Primjenom Ohmovog zakona (U=I·R) formule za rad i snagu se mogu pisati:
W
I R t
U
R
t
P
I R
U
R
=
⋅ =
⋅
=
=
2
2
2
2

70
č
nog polja proizvedenog anodnim naponom i dioda služi kao ispravlja
č
. Katodna cijev je
vakuumska elektronska cijev u kojoj uski snop elektrona putuju
ć
i iz katode prolazi kroz
otvor u anodi, otklanja se kroz elektronske plo
č
ice i udara u ekran. Trioda je vakuumska
elektronska cijev koja osim katode i anode ima i tre
ć
u elektrodu, upravlja
č
ku rešetku.
Trioda služi kao poja
č
alo.
MAGNETSKO POLJE
Svaki naboj u gibanju stvara u prostoru magnetsko polje. Jakost magnetskog polja H u
to
č
ki A udaljenoj za r od naboja Q koji se giba brzinom v iznosi (Biot - Savart - Laplaceov
zakon):
H
Q v
r
= ⋅ ⋅
⋅
sin
α
π
4
2
gdje je
α
kut izme
đ
u smjera brzine
v
r
i spojnice
r
r
naboja i promatrane to
č
ke:
Sli
č
no je jakost magnetskog polja elemenata vodi
č
a
Δ
l kroz koji te
č
e struja jakosti I
jednaka:
Δ
Δ
H
I l
r
=
sin
α
π
4
2
Jedinica za jakost magnetskog polja je Am
-1
.
Veza izme
đ
u magnetske indukcije (gusto
ć
e magnetskog toka) i jakosti magnetskog polja je
B=
μ
0
·
μ
r
·H
gdje je
μ
0
=4
π
·10
-7
TmA
-1
permeabilnost vakuma,
μ
r
relativna permeabilnost tvari, tj. omjer
magnetske indukcije u tvari i vakuumu za istu jakost polja:
μ
r
B
B
=
0
71
Za zrak i ve
ć
inu tvari
μ
=
μ
0
jer je
μ
r
≈
1, a za feromagnetske materijale
μ
r
je veliki i ovisan o
magnetskom polju. Jedinica za magnetsku indukciju je tesla (1T).
Magnetsko polje ravnog vodi
č
a
. Jakost magnetskog polja u udaljenosti r od ravnog vodi
č
a
kojim te
č
e struja jakosti I:
dana je izrazom:
H
I
r
=
⋅
2
π
Magnetske silnice ravnog vodi
č
a kroz kojeg te
č
e struja su koncentri
č
ne kružnice koje leže
u ravnini okomitoj na vodi
č
, a središte im je u osi vodi
č
a. Smijer silnica (vektora
H
r
odnosno
B
r
) odre
đ
ujemo pravilom desne ruke. Ako palac pokazuje smjer struje, savijeni
prsti pokazuju smjer silnica magnetskog polja.
Magnetsko polje zavojnice
. Jakost magnetskog polja unutar zavojnice duljine l koja ima N
zavoja kada kroz nju te
č
e jakost struje I dana je izrazom:
H
N I
l
= ⋅
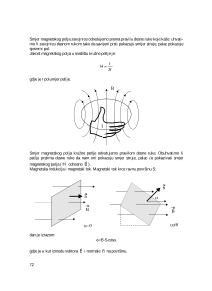
73
Ako silnice magnetskog polja prolaze okomito kroz površinu tok se može prikazati kao:
φ
=B·S
Jedinica za magnetski tok je weber (1 Wb=Tm
2
).
Gibanje elektri
č
ki nabijene
č
estice u magnetskom polju - Lorentzova sila
. Kada se naboj Q
giba brzinom v u magnetskom polju magnetske indukcije B na njega djeluje Lorentzova
sila koja je jadnaka:
F=Q·v·B·sin
α
gdje je
α
kut izme
đ
u smjera gibanja (
v
r
) i smjera vektora (
B
r
).
U slu
č
aju pozitivnog naboja smjer sile odre
đ
ujemo pravilom desnog dlana koje kaže: Ako
ispruženi prsti pokazuju smjer magnetskog polja (
B
r
), a palac smjer brzine
č
estice (
v
r
),
pra-vac sile je okomit na dlan, a smjer te sile je od dlana:
Ako je naboj negativan sila je suprotnog smjera.
Djelovanje magnetskog polja na vodi
č
kojim te
č
e elektri
č
na struja - Amperova sila
.
Veli
č
ina sile F kojom homogeno magnetsko polje magnetske indukcije B djeluje na vodi
č
duljine l kojim te
č
e jakost struje I:
74
jednaka je:
F=B·I·l·sin
α
gdje je
α
kut izme
đ
u smjera kojim te
č
e struja i smjera vektora
B
r
.
Smjer sile (otklona vodi
č
a) odre
đ
ujemo pravilom desnog dlana. Postavimo li desni dlan
tako da prsti pokazuju smjer magnetskog polja B, a palac smjer struje I, sila F
ć
e imati
takav smjer da vodi
č
nastoji udaljiti od dlana.
ELEKTROMAGNETSKA INDUKCIJA
Elektromagnetska indukcija je pojava da se promjenom magnetskog toka u vodi
č
u inducira
napon:
U
N
t
i
= −
Δφ
Δ
Faradayev zakon elektromagnetske indukcije kaže da je inducirani napon proporcionalan
brzini promijene magnetskog toka.
Δφ
je promijena magnetskog toka,
Δφ
=
φ
2
-
φ
1
u svakome od zavoja, a N broj zavoja.
Predznak (-) kaže da je inducirani napon takav da od tog napona stvorena inducirana struja
svojim magnetskim u
č
inkom nastoji poništiti uzrok koji ju je proizveo (Lenzovo pravilo).
Kada se ravni vodi
č
duljine l giba brzinom v u homogenom magnetskom polju magnetske
indukcije B i pod kutem
α
u odnosu na polje, u vodi
č
u se inducira napon koji je jednak:
U
i
= -Blvsin
α
Magnetski tok koji je proizvela struja I koja protje
č
e kroz neki zavoj jednak je:
φ
=L·I
gdje je L koeficijent samoindukcije (induktivitet) koji ovisi o obliku i veli
č
ini zavoja te
magnetskoj permeabilnosti okolnog sredstva.
Jedinica za induktivitet je henri (H)
H=WbA
-1
=VsA
-1
Promjenom jakosti struje kroz zavoj, mijenja se i magnetski tok kroz površinu ograni
č
enu
tim zavojem te se u njemu inducira elektromotorna sila (napon) samoindukcije:
U
t
L
I
t
L
= −
= −
Δφ
Δ
Δ
Δ

76
Ukupan otpor u krugu izmjeni
č
ne struje - impendancija
Z.
Z
R
R
R
L
C
=
+
−
2
2
(
)
Z je impedancija ili ukupni otpor, R je radni otpor, R
L
=L·
ω
je induktivni otpor, R
C
C
=
⋅
1
ω
je kapacitivni otpor. R
L
i R
C
su takozvani prazni otpori.
Ohmov zakon za krug izmjeni
č
ne struje glasi:
I
U
Z
=
Razlika faze
ϕ
izme
đ
u izmjeni
č
nog napona i izmjeni
č
ne struje:
dana je izrazom:
tg
R
R
R
L
C
ϕ =
−
Srednja vrijednost snage izmjeni
č
ne struje je dana izrazom:
P=I·U·cos
ϕ
77
Elektromagnetski titraji i valovi
. Elektri
č
ni titrajni krug se sastoji od zavojnice induktiviteta
L i kondenzatora kapaciteta C:
Vlastita frekvencija takvog titrajnog kruga je dana Thomsonovom formulom:
f
LC
=
1
2
π
Elektromagnetski valovi nastaju širenjem titraja elektri
č
nog i magnetskog polja iz titrajnog
kruga u prostor. Vektori elektri
č
nog i magnetskog polja u valu su uvijek me
đ
usobno
okomiti, a okomiti su i na smjer širenja vala. Valna duljina, frekvencija i brzina su poveza-
ne identi
č
nim izrazom kao i kod mehani
č
kih valova:
v=
λ
·f
Brzina širenja elektromagnetskih valova u vakumu dana je relacijom:
C
=
1
0
0
ε μ
gdje je
ε
0
=8,85·10
-12
Fm
-1
, a
μ
0
=4
π
·10
-7
Hm
-1
.
Brzina širenja elektromagnetskih valova u bilo kojem drugom sredstvu ovisi o njegovim
elektromagnetskim svojstvima i odre
đ
ena je izrazom:
v
c
r
r
=
=
1
εμ
ε μ
Transformator
. Ure
đ
aj koji transformira izmjeni
č
nu struju jednog napona i jakosti u izmje-
ni
č
nu struju drugog napona i jakosti a radi na principu elektromagnetske indukcije. Za
idealni transformator bez gubitaka vrijedi:
U
U
I
I
N
N
1
2
2
1
1
2
=
=
gdje su U
1
, I
1
i N
1
napon, jekost i broj namotaja primarne zavojnice, a U
2
, I
2
i N
2
napon,
jakost i broj namotaja sekundarne zavojnice.

79
5. U nekoj žici otpora 20
Ω
razvijena je toplina od 900 J u vremenu od 5 s. Naboj elektrona
je 1,6·10
-19
C. Broj elektrona koji su u to vrijeme prošli kroz presjek žice je:
R=20
Ω
W=900 J
t=5 s
n=?
W
I R t
I
W
R t
n Q
t
W
R t
n
t
Q
W
R t
s
C
J
s
e
e
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
⋅
⋅
=
⋅
−
2
19
19
5
1 6 10
900
20
5
9 375 10
,
,
Ω
6. Dva naboja Q
1
=4·10
-8
C i Q
2
=2,5·10
-8
C nalaze se u zraku na udaljenosti 1 m. Koliki rad
treba izvršiti da bi ih približili na udaljenost 0,2 m? (
ε
0
=8,85·10
-12
C
2
N
-1
m
-2
)
Q
1
=4·10
-8
C
Q
2
=2,5·10
-8
C
R
1
=1 m
R
2
=0,2 m
W=?
W
E
Q
Q
R
Q
Q
R
Q
Q
R
R
W
C
C
C N
m
m
m
W
J
p
=
=
⋅
−
⋅
=
⋅
−
⎛
⎝
⎜
⎞
⎠
⎟
=
⋅
⋅
⋅
⋅
⋅
⋅
−
⎛
⎝
⎜
⎞
⎠
⎟
=
⋅
−
−
−
−
−
−
Δ
1
2
0
2
1
2
0
1
1
2
0
2
1
8
8
12
2
1
2
5
4
4
4
1
1
4 10
2 5 10
4 3 14 8 85 10
1
0 2
1
1
3 59 10
πε
πε
πε
,
,
,
,
,
7. Napon izme
đ
u horizontalnih plo
č
a kondenzatora je 10 V, a razmak plo
č
a je 0,1 m. Mi-
kroskopski vidljiva kapljica ulja mase 10
-13
kg lebdi u elektri
č
nom polju. Naboj kapljice je:
U=10 V
d=0,1 m
m=10
-13
kg
Q=?
Q E
m g
Q
m g
E
E
U
d
Q
m g d
U
kg
ms
m
V
C
⋅ = ⋅
=
⋅
=
=
⋅ ⋅ =
⋅
⋅
=
⋅
−
−
−
10
9 81
0 1
10
9 81 10
13
2
15
,
,
,
8. Elektri
č
na pe
ć
je priklju
č
ena na gradsku mrežu napona 220 V. Pe
ć
ima 3 m dugu grija
ć
u
nit i za 20 min povisi u prostorijama temperaturu za 20°C. Koliko mora biti duga
č
ka ta nit
ako isto povišenje temperature u prostoriji želimo posti
ć
i za 15 min?
U=220 V
l
1
=3 m
t
1
=20 min=1200 s
Δ
T=20 K
t
2
=15 min=900 s
l
2
= ?
80
W = U I t =
U
U
U
2
2
2
⋅ ⋅
⋅
⋅
=
⋅
=
=
=
t
R
t
R
t
R
R
R
t
t
R
R
R
R
1
1
2
2
1
2
1
2
1
2
2
1
20
15
3
4
min
min
R
R
l
S
l
S
l
l
l
m
l
m
2
1
2
1
2
1
2
2
3
4
3
4
3
4
3
4
3
2 25
=
/ ⋅
/
= ⋅ /
⋅
/
=
= ⋅
=
ρ
ρ
,
9. U homogenom magnetskom polju indukcije 1,5 T jednoliko se giba vodi
č
duljine 10 cm.
Njime te
č
e struja 2 A, brzina mu je 1ms
-1
, a vodi
č
je okomit na polje. Snaga potrebna ua
ovo gibanje jest?
α
=90°°
B=1,5 T
l=10 cm=0,1 m
I=2 A
v=1 ms
-1
P=?
P=F·v=B·I·l·sin
α
·v= B·I·l·v=1,5 T·2 A·0,1 m·1 ms
-1
=0,3 W
10. Proton se giba po kružnoj stazi polumjera 3,34 cm, u magetskom polju indukcije 0,1 T.
Kolika je brzina protona?
R=3,34 cm
B=0,1 T
v=?
mv
R
Q v B
v
Q B R
m
C
T
m
kg
ms
2
19
2
27
5
1
1 6 10
0 1
3 34 10
1 67 10
3 2 10
= ⋅ ⋅
= ⋅ ⋅ =
⋅
⋅
⋅
⋅
⋅
=
⋅
−
−
−
−
,
,
,
,
,
11. Zavojnica koeficijenata samoindukcije 0,1 H i omskog otpora 51
Ω
priklju
č
ena je na
izvor izmjeni
č
nog napona efektivne vrijednosti 120 V i frekvencije 50 Hz. Kolika efektiv-
na struja te
č
e zavojnicom?
L=0,1 H
R=51
Ω
U
ef
=120 V
ν
=50 Hz
I
ef
=?

82
15. Titrajni krug
č
ini kondenzator kapaciteta 50 pF i zavojnica induktiviteta 0,2 mH. Odre-
dite valnu duljinu na koju je ugo
đ
en?
C=50 pF=50·10
-12
F
L=0,2 mH=0,2·10
-3
H
λ
=?
ν
π
λ
ν
π
λ
=
⋅
= = ⋅
⋅
= ⋅
⋅ ⋅
⋅
⋅
⋅ ⋅
=
−
−
−
1
2
2
3 10
2 3 14
0 2 10
50 10
188 4
8
1
3
12
L C
c
c
L C
ms
H
F
m
,
,
,
16. Transformator za elektri
č
no zvonce smanjuje izmjeni
č
ni napon s 220 V na 4 v. Sekun-
darna zavojnica ima 12 zavoja. Koliko zavoja ima primarna zavojnica?
U
1
=220 V
U
2
= 4 V
N
2
=12
N
1
=?
U
N
U
N
N
U
U
N
V
V
1
1
2
2
1
1
2
2
220
4
12
660
=
=
⋅
=
⋅ =
83
OPTIKA
GEOMETRIJSKA OPTIKA
Ravno zrcalo
je glatka i ravna reflektiraju
ć
a površina.
Zakon refleksije
svjetlosti glasi: Upadna i reflektirana zraka svjetlosti su u istoj ravnini kao
i normala na reflektiraju
ć
u površinu a kut upada
α
jednak je kutu refleksije
β
:
Slika je u ravnom zrcalu jednake veli
č
ine kao i predmet, virtualna i simetri
č
na predmetu s
obzirom na ravninu zrcala:
Sferno zrcalo
Sferno zrcalo je dio kugline plohe pa je reflektiraju
ć
a površina zakrivljena - udubljena ili
izbo
č
ena. Jednadžba sfernog zrcala je:
1
1
1
x
x
f
+
′
=

85
Kod tog prijelaza frekvencija ostaje nepromijenjena a valna duljina i brzina se mijenjaju.
Apsolutni indeks loma nekog sredstva n je omjer brzine svjetlosti (c) u vakuumu i brzine
svjetlosti v u tom sredstvu:
n
c
v
=
Relativni indeks loma sredstva 2 prema sredstvu 1 je:
n
n
n
v
v
2 1
2
1
1
2
,
=
=
gdje je v
1
brzina svjetlosti u sredstvu 1, a v
2
brzina svjetlosti u sredstvu 2. Ravnina koja
odvaja dva sredstva se zove ravni dioptar.
Pri prijelazu zrake svjetlosti iz sredstva indeksa loma n
1
u sredstvo indeksa loma n
2
, upadna
i lomljena zraka kao i normala na granici tog sredstva u upadnoj to
č
ki su u istoj ravnini.
Snelliusov zakon loma povezuje kut upada
α
i kut loma
β
:
n
n
n
2 1
2
1
,
sin
sin
=
=
α
β
Totalna refleksija
. Ako svjetlost prelazi iz opti
č
ki guš
ć
eg u opti
č
ki rije
đ
e sredstvo kut loma
β
>
α
, dakle svjetlost se lomi od okomice. Kut loma može biti najviše 90°, i za taj kut kaže-
mo da je kut upada tzv. grani
č
ni. (
α
g
) Ako je kut upada ve
ć
i od
α
g
svjetlost ne prelazi u
drugo sredstvo ve
ć
se reflektira. Ta pojava se zove totalna refleksija.
sin
α
g
n
n
=
2
1
Ako svjetlost prelazi iz sredstva indeksa loma n u vakuum vrijedi:
sin
g
α =
1
n
Planparalelna plo
č
a
je homogeno opti
č
ko sredstvo, ome
đ
eno dvjema ravnim paralelnim
plohama. Prolazom kroz planparalelnu plo
č
u zraka svjetlosti ne mijenja smjer ve
ć
je samo
pomaknuta paralelno samoj sebi:
86
Prizma
je opti
č
ko sredstvo ome
đ
eno s dvije ravnine koje zatvaraju kut A:
Kut devijacije
δ
pri prolazu kroz opti
č
ku prizmu dan je relacijom:
δ
=
α
1
+
α
2
-A
gdje su
α
1
kut upada,
α
2
kut pod kojim zraka izlazi iz prizme, a A kut prizme. Prolazom
kroz prizmu bijela svjetlost se rastavlja na dugine boje (spektar) jer brzina svjetlosti u
nekom prozirnom sredstvu ovisi o valnoj duljini a time i indeks loma, te se svjetlost razli
č
i-
tih boja (razli
č
itih
λ
) i razli
č
ito lomi.
Le
ć
e
Le
ć
e su prozirna tijela, ome
đ
ena s dvije sferne plohe od kojih jedna može biti i ravna.
Tankim le
ć
ama nazivamo le
ć
e kod kojih je razmak izme
đ
u dioptrijskih ploha u sredini le
ć
e
malen u odnosu na promjer le
ć
e. Opti
č
ka os le
ć
e je pravac koji prolazi kroz središta
zakrivljenosti sfernih ploha le
ć
e. Razlikujemo dvije vrste le
ć
a:

88
Pove
ć
anje le
ć
e je omjer veli
č
ine slike y' i veli
č
ine predmeta y:
m
y
y
x
x
= ′ = − ′
Ako je pove
ć
anje pozitivno, slika je uspravna, a ako je pove
ć
anje negativno slika je obrnu-
ta. Kada je m>1 slika je ve
ć
a od predmeta, a kada je m<1 slika je manja od predmeta.
Jakost le
ć
e je recipro
č
na vrijednost žarišne daljine:
j
f
=
1
Jakost le
ć
e se mjeri u dioptrijama (1 dpt=1 m
-1
). Konvergentne le
ć
e imaju pozitivnu jakost
(+dioptrije), a divergentne le
ć
e imaju negativnu jakost (-dioptrije).
89
FIZIKALNA OPTIKA
Svjetlost je transferzalni elektromagnetski val
č
ija je brzina u vakuumu:
c=2,997925·10
8
ms
-1
≈
3·10
8
ms
-1
Valnu prirodu svjetlosti potvr
đ
uju pojave interferencije, ogiba i polarizacije.
Interferencija
Interferencija nastaje zbrajanjem dvaju ili više valova svjetlosti jednake frekvencije i
konstantne razlike u fazi (tzv. koherentnih valova). Rezultat tog zbrajanja je poja
č
anje
intenziteta u u nekim to
č
kama prostora, odnosno smanjenje u drugim.
Poja
č
anje
ć
e nastati ako razlika opti
č
kih puteva dviju zraka
δ
=k·
λ
(k=0, 1, 2...), dok
ć
e
destruktivna interferencija (minimum rasvjete) nastati na mjestima gdje je:
δ
λ
=
+ ⋅
(
)
2
1
2
k
(k=0, 1, 2, ...)
Na slici su prikazana dva koherentna izvora. U to
č
ki M
1
dolazi do interferencije svjetlosti
koja ide iz izvora koji su me
đ
usubno razmaknuti za udaljenost d, a to
č
ka M
1
se nalazi na
zastoru udaljenom a od izvora. Opti
č
ka razika puteva zrake koja ide iz izvora jedan i zrake
iz drugog izvora jednaka je geometrijskoj razlici pomnoženoj s indeksom loma sredstva
kroz koje je zraka prolazila:
δ
=nr
1
-nr
2
Rezultantni intenzitet pri interferenciji ovisi o fazi, odnosno o razlici opti
č
kih putova
valova koji interferiraju. Razmak izme
đ
u dviju svjetlih ili tamnih interferiranih pruga na
zastoru paralelnom s dva koherentna izvora jest:
s
a
d
= ⋅λ

91
RIJEŠENI PRIMJERI IZ PODRU
Č
JA OPTIKA
1. Indeks loma vode je 1,33. Koliki je grani
č
ni kut totalne refleksije?
n=1,33
α
g
=?
sin
,
,
α
g
n
= =
=
=
′
1
1
1 33
0 75187
48 45
o
2. Okomito na opti
č
ku rešetku konstante 10
-5
m upada komponenta svjetlosti dviju valnih
duljina: 444 nm i 592 nm. Pod kojim
ć
e se najmanjim kutom ogiba pokriti maksimumu
obiju linija?
d=10
-5
m
λ
1
=444 nm
λ
2
=592 nm
α
K
=?
d
k
d
k
k
k
k
k
nm
nm
k
k
d
d
m
m
k
k
k
k
k
sin
sin
,
sin
sin
,
,
α
λ
α
λ
λ
λ
α
λ
α
λ
α
= ⋅
= ′ ⋅
⇒
′
=
′
=
=
=
=
′ =
= ⋅
=
⋅
= ⋅
⋅
=
=
−
−
1
2
2
1
1
1
9
5
592
444
1 333
4
3
4
3
4
4
4 444 10
10
0 1776
10 23
o
3. Predmet na opti
č
koj osi je 40 cm od tjemena konkavnog sfernog zrcala polumjera
zakrivljenosti 50 cm. Odredite položaj slike.
x=40 cm
R=50 cm
x'=?
1
1
1
1
40
1
1
25
1
1
25
1
40
8 5
200
200
3
66 67
x
x
f
cm
x
cm
x
cm
cm
cm
x
cm
cm
+
′
=
+
′
=
′
=
−
=
−
′ =
=
,
4. Kolika je jakost konvergentne le
ć
e žarišne daljine 25 cm?
f=25 cm=0,25 m
j=?
j
f
m
dpt
= =
=
1
1
0 25
4
,
92
5. S le
ć
om žarišne daljine 6 cm, koja služi kao lupa, želimo promatrati mali predmet duljine
2 mm, tako da njegova virtuelna slika bude 5 mm. Koliko mora le
ć
e biti udaljena od
predmeta?
f=6 cm
y=2 mm
y'=5 mm
x=?
− ′ = ′
− ′ =
′ = −
x
x
y
y
x
x
mm
mm
x
x
5
2
2 5
,
1
1
1
1
1
2 5
1
6
1
2
5
1
6
5 2
5
1
6
5
3 6
3 6
x
x
f
x
x
cm
x
x
cm
x
cm
x
cm
x
cm
+
′
=
−
=
−
=
− =
= ⋅
=
,
,
6. Zraka svjetlosti upada iz zraka na prozirni materijal pod kutom 56°. Koliki je indeks
loma ako lomljena i reflektirana zraka zatvaraju kut od 90°?
α
=56°
n=?
n=tg
α
=tg56°=1,4825
7. U teku
ć
ini iznad koje je zrak, totalna refeksija opaža se pod kutem od 30°. Kolika je
brzina svjetlosti u toj teku
ć
ini?
α
g
=30°
v=?
sin
α
g
n
n
n
=
=
=
1
1
1
2
2
n
c
v
v
c
n
ms
v
ms
=
= = ⋅
=
⋅
−
−
3 10
2
1 5 10
8
1
8
1
,
8. Zraka svjetlosti koja upada pod kutem 45° na ravninu stakla, djelomi
č
no se lomi, a djelo-
mi
č
no se reflektira. Kut izme
đ
u lomljene i reflektirane zrake je 107°. Odredi indeks loma
stakla.
α
=45°
γ
=107°
n=?
α β γ
β
α
β
+ + =
=
−
−
=
=
=
=
180
180
107
45
28
45
28
1 506
o
o
o
o
o
o
o
n
sin
sin
sin
sin
,

94
kao kineti
č
ka energija elektrona. Energija izba
č
nog elektrona se može na
ć
i odre
đ
uju
ć
i
napon U potreban za njegovo zaustavljanje, tzv. napon zaustavljanja te je:
mv
e U
2
2
= ⋅
Zaustavlajnjem brzih elektrona nastaje rendgensko zra
č
enje. Kod toga se energija elektrona
djelomi
č
no ili potpuno pretvoriti u energiju fotona rendgenskih (x) zraka:
h
h c
mv
e U
g
ν
λ
= ⋅ =
= ⋅
min
2
2
pa slijedi da je:
λ
min
= ⋅
⋅
h c
e U
gdje je
λ
min
grani
č
na valna duljina rendgenskih zraka.
BOHROV MODEL ATOMA
Prema prvom Bohrovom postulatu elektron se može gibati oko jezgre samo po odre
đ
enim
stazama polumjer kojih je:
r
n
h
m e
n
e
=
⋅
2
0
2
2
ε
π
gdje je n glavni kvantni broj (n=1, 2, 3...), h je Planckova konstanta,
ε
0
permitivnost vakuu-
ma, m
e
masa elektrona, e naboj elektrona. Energija elektrona u n-toj stazi je:
E
n
m e
h
n
e
= −
1
8
2
4
0
2
2
ε
(n=1, 2, 3, ...)
Brzina elektrona u n-toj stazi je:
v
e
n
h
n
=
2
0
2
ε
Prema drugom Bohrovom postulatu frekvencija emitirane svjetlosti kad elektron prelazi iz
n-te u m-tu stazu se može odrediti iz izraza:
h
ν
nm
=E
n
-E
m
95
ν
ε
nm
n
m
e
E
E
h
m e
h
m
n
=
−
=
−
⎛
⎝⎜
⎞
⎠⎟
4
0
2
3
2
2
8
1
1
ZRA
Č
ENJE CRNOG TIJELA
Sva tijela zra
č
e energiju. Spektar zra
č
enja ovisi o temperaturi tijela. Apsolutno crno tijelo
potpuno apsorbira upadnu energiju ali to tijelo je najbolji emiter za odre
đ
enu temperaturu.
Toplinska energija koju zra
č
i površina apsolutno crnog tijela u 1 sekundi može se odrediti
Stefan - Boltzmanovim (Štefan - Bolcmanovim) zakonom:
P=
σ
·ST
4
gdje je P snaga zra
č
enja, T temperatura tijela, S površina tijela, a
σ
Stefan-Boltzmanova
konstanta:
σ
=5,67·10
-8
Wm
-2
K
-4
Prema Wienovu (Vin) zakonu valna duljina kojoj pripada maksimalna energija zra
č
enja
apsolutno crnog tijela je obrnuto razmjerna termodinami
č
koj temperaturi:
λ
max
·T=c=2,9·10
-3
mK
tj. umnožak valne duljine kod koje je maksimalna energija zra
č
enja (
λ
max
) i termodinami-
č
ke temperature (T) je jednak konstantoj veli
č
ini.
EKVIVALENT MASE I ENERGIJE
Prema teoriji relativnosti masa tijela se mijenja s brzinom, te je masa tijela koje se giba
ve
ć
a od mase koja miruje:
m
m
v
c
=
−
0
2
2
1
gdje je m masa u gibanju, m
0
masa u mirovanju, v brzina tijela i c brzina svjetlosti. Ako je
masa tijela u mirovanju m
0
, a kad se giba brzinom v masa mu je m, onda je njegova kineti-
č
ka energija jednaka:
E
m v
m
m
c
k
=
=
−
⋅
0
2
0
2
2
(
)

97
Unificiranoj atomskoj jedinici mase prema Einsteinovoj relaciji E=m·c
2
odgovara energija
od 931,50 MeV.
RADIOAKTIVNI RASPAD
Jezgra ili nukleus nekog elementa može se prirodnim putem promijeniti (govorimo o
radioaktivnom raspadu). Vrijeme poluraspada T
1/2
je vrijeme potrebno da se od po
č
etne
koli
č
ine radioaktivnog izotopa raspadne polovica. Radioaktivni raspad karakterizira i
konstanta raspadanja
λ
:
λ =
=
ln
,
2
0 693
1
2
1
2
T
T
Zakon radioaktivnog raspadanja kaže:
N
N
e
N
e
N
t
t
T
t
T
=
⋅
=
⋅
=
⋅
−
−
−
0
0
0 693
0
1
2
1
2
2
λ
,
gdje je N
0
po
č
etni broj neraspadnutih atoma u vrijeme t=0, N broj atoma koji se nakon
vremena t nisu raspali, e=2,71828 je baza prirodnog logaritma, T
1/2
vrijeme poluraspada i
λ
konstanta raspadanja.
Aktivnost radioaktivne tvari je:
A
N
t
N
= −
=
Δ
Δ
λ
i mjeri se bekerelima (Bq). Ta aktivnost vremenom opada prema zakonu:
A
A
e
t
T
=
⋅
−
0
0 693
1
2
,
gdje je A
0
aktivnost u vremenu t=0, a A aktivnost u vremenu t.
Nuklearne reakcije
Jezgre atoma se mogu promijeniti i umjetnim putem, pomo
ć
u nuklearnih reakcija. Pri tim
reakcijama neka
č
estica a bombardira jezgru X te tada nastaje jezgra Y i oslobodi se
č
estica
b što se sibmoli
č
ki piše:
a+X
→
Y+b ili X(a, b)Y
Č
estice koje bombardiraju jezgru (a) mogu biti: neutroni n, protoni p, deuteroni d (jezgre
od
1
2
H ), tritoni t (jezgre od
1
3
H ),
α
č
estice (jezgre od
2
4
He ), elektroni e
−
, pozitroni e
+
,
γ
č
estice i dr. Pri svakoj nuklearnoj reakciji zbroj masenih brojeva A i rednih brojeva Z prije i
poslije rekcije mora biti jednak. Energetski ekvivalent razlike ukupne mase prije i poslije
reakcije je, tzv. Q vrijednost nuklearne reakcije.
98
α
- raspad
Z
A
Z
A
X
Y
He
→
+
−
−
2
4
2
4
Kod
α
raspada se redni broj novo nastalog nuklida umanjuje za 2, a maseni za 4.
β
-
-raspad
Z
A
Z
A
X
Y
e
→
+
+
−
1
1
0
Pri
β
raspadu redni broj novonastalog nuklida je za 1 ve
ć
i a maseni broj ostaje nepromije-
njen.
β
+
- raspad
Z
A
Z
A
X
Y
e
→
+
−
+
1
1
0
Novo nastali nuklid
β
+
raspadom ima redni broj za 1 manji a isti maseni broj.
Pri pretvorbi elektrona i pozitrona u elektromagnetsko zra
č
enje sva se njihova masa pretva-
ra u energiju te nastaje 2
γ
kvanta
e
e
−
+
+
=
2
γ
Obrnuto
γ
kvant dovoljne energije pri sudaru s jezgrom pretvara se u par elektron-pozitron
γ =
+
−
+
e
e

100
5. Kolika je maksimalna valna duljina svjetlosti koja još pobu
đ
uje fotoelektri
č
ni efekt u
litijevoj fotokatodi? (izlazni rad je 3,96·10
-19
J, h=6,626·10
-34
Js, c=3·10
8
ms
-1
)
Wi=3,96·10
-19
J
λ
=?
E
W
E
E
h c
W
f
i
k
k
i
=
+
=
⋅ =
0
λ
λ = ⋅ =
⋅
⋅ ⋅
⋅
=
⋅
=
−
−
−
−
h c
W
Js
ms
J
m
nm
i
6 626 10
3 10
3 96 10
5 019 10
502
34
8
1
19
7
,
,
,
6. Koliko se fisija dogodi svake sekunde u reaktoru koji kao gorivo koristi
235
U, ako je
toplinska snaga tog reaktora 1800 MW? (Pretpostavite da se pri fisiji svake jezgre
235
U
oslobodi 200 MeV)
t=1 s
P=1800MW
E=200 MeV=200·10
6
·1,6·10
-19
J
n=?
n
P t
E
W s
J
= ⋅ =
⋅
⋅
⋅
⋅
=
⋅
−
1800 10
1
200 1 6 10
5 625 10
6
13
19
,
,
7. Vrijeme poluraspada radioaktivnog izotopa
90
Sr je 28 godina. Za koje vrijeme
ć
e se
aktivnost nekog uzorka tog izotopa smanjiti 8 puta?
T
1/2
=28 god
A=A
0
/8
t=?
A
A
t
T
=
⋅
−
0
2
1
2
A
A
t
god
t
god
0
0
28
3
28
8
2
2
2
=
⋅
=
−
−
−
t
god
t
god
god
28
3
3 28
84
=
= ⋅
=
8. Ako je pri brzini 1,46 km/s valna duljina elektrona 500 nm, kolika je valna duljina pri
brzini elektrona 0,024 c, gdje je c brzina svjetlosti
v
1
=1,46 km/h=1460ms
-1
λ
1
=500 nm=500·10
-9
m
v
2
=0,024·c=0,024·3·10
8
ms
-1
λ
2
=?
101
λ
λ
1
1
2
2
=
=
h
mv
h
mv
λ
λ
λ
λ
λ
2
1
2
1
1
2
2
1
2
1
3
1
9
8
1
2
9
1 46 10
500 10
0 024 3 10
0 101 10
0 1
=
=
=
⋅
=
⋅
⋅
⋅
⋅ ⋅
=
⋅
=
−
−
−
−
h
mv
h
mv
v
v
v
v
ms
m
ms
m
nm
,
,
,
,
9. Laserski snop valne duljine 325 nm izbacuje elektrone iz cezijeve plo
č
ice (fotoefekt) koji
se zaustavljaju naponom 1,91 V. Koliki je rad izlaza cezija? (h=6,625·10
-34
Js, e=1,6·10
-19
C)
λ
=325 nm
U=1,91 V
W
i
=?
E
h c
W
E
E
Q
U
W
h c
Q
U
Js
ms
m
C
V
i
k
k
e
i
e
= ⋅ =
+
=
⋅
= ⋅ −
⋅ =
⋅
⋅ ⋅
⋅
−
⋅
⋅
−
−
−
−
λ
λ
6 625 10
3 10
325 10
1 6 10
1 91
34
8
1
9
19
,
,
,
W
J
i
=
⋅
−
⋅
=
⋅
−
−
−
6 11 10
3 056 10
3 054 10
19
19
19
,
,
,
W
J
C
eV
i
=
⋅
⋅
=
−
−
3 054 10
1 6 10
1 91
19
19
,
,
,
10. Valna duljina argonove crvene linije je 679 nm. Koliki je izlazni rad materijala kojemu
je to grani
č
na valna duljina? (h=6,63·10
-34
Js)
λ
=679 nm
W
i
=?
h c
W
i
⋅ =
λ
W
Js
ms
m
J
W
J
C
eV
i
i
=
⋅
⋅ ⋅
⋅
=
⋅
=
⋅
⋅
=
−
−
−
−
−
−
6 63 10
3 10
679 10
2 929 10
2 929 10
1 6 10
1 83
34
8
1
9
19
19
19
,
,
,
,
,
11. Da bi se masa
č
estice utrostru
č
ila,
č
estica se mora gibati brzinom?
m=3m
0
v=?

103
ZADACI
104

106
E) u težište tijela
rješenje:
(A)
6. Njihalo u
č
ini 30 titraja u minuti. Vrijeme izme
đ
u dva uzastopna položaja sa elongacijom
jednakoj nuli je:
A) 4 s
B) 3 s
C) 2 s
D) 1 s
E) 1/2 s
rješenje:
(D)
f=30 min
-1
T/2=?
T
f
s
s
T
s
= =
=
⇒
=
1
1
30
60
2
2
1
Za vrijeme jednog titraja njihalo dva puta pro
đ
e kroz položaj ravnoteže.
7. Tlaku od 1 Pa odgovara na zemlji tlak stupca vode visine:
A) 0,102 mm
B) 1,02 mm
C) 10,2 mm
D) 102 mm
E) 1020 mm
rješenje:
(A)
P=1 Pa
h=?
P
s h
g
s
h
P
g
Pa
kgm
ms
mm
=
⋅ ⋅ ⋅
⇒
=
=
⋅
=
−
−
ρ
ρ
1
1000
9 81
0 102
3
2
,
,
8. Izmjeni
č
ni napon maksimalne vrijednosti 100 V i frekvencije 100 Hz priklju
č
en je na
potroša
č
otpora 10
Ω
. Struja kroz potroša
č
je dana sa:
A) I=(10 A) sin (628 s
-1
)t
B) I=(0,1 A) sin (314 s
-1
)t
C) I=(0,1 A) sin (628 s
-1
)t
D) I=(10 A) sin (100 s
-1
)t
E) I=(0,1 A) sin (100 s
-1
)t
rješenje:
(A)
U
0
=100 V
f=100 Hz
R=10
Ω
I
0
=?
I=I
o
sin
ω
t
I=I
o
sin 2
π
ft
I=(10 A)sin (628 s
-1
)t
I
U
R
V
A
0
0
100
10
10
=
=
=
Ω
9. Lorenzova sila na naboj koji se giba okomito na magnetsko polje je:
A) Qv/B
B) Q/vB
C) 1/QvB
D) QvB
107
E) vB/Q
rješenje:
(D)
10. Inducirani napon u jednom zavoju razmjeran je:
A) magnetskom polju
B) gusto
ć
i magnetskog toka
C) magnetskom toku
D) vremenu u kojem se promijeni magnetski tok
E) brzini promjene magnetskog toka
rješenje:
(E)
11. U titrajnom krugu nastaju titraji frekvencije 10 MHz. Koliko traje jedan titraj?
A) 100
μ
s
B) 100 ns
C) 0,1 ns
D) 100 ps
E) 100 ms
rješenje:
(B)
f=10 MHz
T=?
T
f
Hz
s
s
ns
= =
⋅
=
⋅
=
⋅
=
−
−
1
1
10 10
0 1 10
100 10
100
6
6
9
,
12. Koliki je otpor (u omima) željezne žice presjeka 0,01 mm
2
, duljine 10 m. Otpornost
željeza je 0,1·10
-6
Ω
m.
A) 10
B) 100
C) 1000
D) 10000
E) 100000
rješenje:
(B)
s=0,01 mm
2
l=10 m
ρ
=0,1·10
-6
Ω
m
R=?
R
l
s
m
m
m
=
⋅
=
⋅
⋅
⋅
=
−
−
ρ
0 1 10
10
0 01 10
100
6
6
2
,
,
Ω
Ω
13. Kroz grijalicu snage 2000 W te
ć
e struja od 20 A. Koliki je otpor grijalice (u
Ω
)?
A) 100
B) 0,01
C) 500
D) 50
E) 5
rješenje
(E)
P=2000 W
I=20 A
R=?
P=U
⋅
I
⇒
=
U
P
I
R
U
I
P
I
W
A
=
=
=
=
2
2
2000
20
5
(
)
Ω

109
19. Vrijeme poluraspada nekog radioaktivnog elementa je 15 minuta. Od po
č
etnog broja
radioaktivnih jezgara ostat
ć
e približno 1/1000 nakon:
A) 0,5 sati
B) 1 sat
C) 2,5 sati
D) 5 sati
E) 25 sati
rješenje (C)
T
1/2
=15 min
N
N
=
1
1000
0
t=?
N
N
N
N
N
N
t
T
t
T
s
s
sati
t
T
t
T
t
T
=
⋅
=
=
=
−
= −
=
= ⋅ ⋅
=
=
−
−
−
−
−
0
0
3
0
0
3
1
2
1
2
2
2
10
2
10
2
3
3
2
3 15 60
0 30103
8969
2 5
1
2
1
2
1
2
log
log
log
,
,
20. Naziv jedinice u SI za napon je:
A) volt
B) kulon
C) henri
D) farad
E) simens
rješenje
(A)
21. Stupcu vode od 10 cm odgovara na zemlji tlak od (Približno! g=10 ms
-2
)
A) 0,1 Pa
B) 1 Pa
C) 10 Pa
D) 100 Pa
E) 1000 Pa
rješenje:
(E)
h=10 cm P=
ρ⋅
g
⋅
h=10
3
kgm
-3
⋅
10ms
-2
⋅
0,1m=10
3
Pa=1000 Pa
P=?
22. Pri polasku sa stanice tramvaj se giba jednoliko ubrzano. Na putu od 50 m postig-ne
brzinu od 10 ms
-1
. Kolika je akceleracija?
A) 1 ms
-2
B) 2 ms
-2
110
C) 0,1 ms
-2
D) 0,2 ms
-2
E) 0,5 ms
-2
rješenje:
(A)
s=50 m
v=10 ms
-1
a=?
v
as
a
v
s
ms
m
ms
=
⇒
=
=
⋅
=
−
−
2
2
10
2 50
1
2
1
2
2
(
)
23. Njihalo u
č
ini 15 njihaja u minuti. Kolika je frekvencija?
A) 4 s
-1
B) 2 s
-1
C) 1 s
-1
D) 1/8 s
-1
E) 1/2 s
-1
rješenje:
(D)
n=15 njihaja/min
f=?
f
n
s
s
s
= =
⋅
=
=
−
−
2
15
2 60
0 125
1
8
1
1
,
24. Jedna litra žive ima masu 13,6 kg. Kolika je gusto
ć
a žive?
A) 1,36·10
-2
kgm
-3
B) 1,36·10
-1
kgm
-3
C) 1,36·10
2
kgm
-3
D) 1,36·10
3
kgm
-3
E) 1,36·10
4
kgm
-3
rješenje:
(E)
m=13,6 kg
V=1 l
ρ
=?
ρ =
=
=
⋅
=
⋅
−
−
−
m
V
kg
m
kgm
kgm
13 6
10
13 6 10
1 36 10
3
3
3
3
4
3
,
,
,
25. Izraz za brzinu pri jednoliko ubrzanom gibanju duž pravca uz po
č
etnu brzinu v
o
je:
A) v
o
t
B) v
o
+at
2
/2
C) v
o
-at
2
/2
D) v
o
+at
E) v
o
-at
rješenje:
(D)
26. Prefiks
μ
(mikro) ima zna
č
enje:
A) 10
6
B) 10
-6
C) 10
9
D) 10
-9
E) 10
12
rješenje:
(B)

112
D) 15 N
E) 21 N
rješenje:
(D)
F
1
=9 N
F
2
=12 N
R=?
R
F
F
N
N
N
N
N
N
=
+
=
+
=
+
=
=
1
2
2
2
2
2
2
2
2
9
12
81
144
225
15
(
)
(
)
32. Izraz za put pri jednoliko usporenom gibanju duž pravca, uz po
č
etnu brzinu v
o
je:
A) v
0
t
B) v
0
t+at
2
/2
C) v
0
t-at
2
/2
D) v
0
t
1
+v
0
t
2
+v
0
t
3
+...
E) at
2
/2
rješenje:
(C)
33. Uteg mase 100 g obješen je o dinamometar sa skalom u N. Koju silu pokazuje? (g=9,8
ms
-2
)
A) 0,098 N
B) 0,98 N
C) 9,8 N
D) 98 N
E) 980 N
rješenje:
(B)
m=100 g
G=?
G=m·g=0,1 kg·9,8 ms
-2
=0,98 N
34. Tijelo mase 1 kg koje slobodno pada na kraju puta od 5 m ima kineti
č
ku energiju:
A) 1000 J
B) 100 J
C) 10 J
D) 50 J
E) 500 J
rješenje:
(D)
m=1 kg
s=5 m
E
k
=?
v
gs
v
ms
m
v
ms
=
=
⋅
⋅
=
−
−
2
2 10
5
10
2
1
E
mv
E
kg
m s
E
J
k
k
k
=
=
⋅
=
−
2
2
2
2
1
100
2
50
35. Koliko je elektri
č
no polje izme
đ
u plo
č
a kondenzatora me
đ
usobno udaljenih 2 mm ako
je na plo
č
ama napon od 2 V?
A) 1 Vm
-1
B) 1 kVm
-1
C) 1 mVm
-1
113
D) 10 Vm
-1
E) 10 kVm
-1
rješenje:
(B)
d=2 mm
U=2 V
E=?
E
U
d
V
m
kVm
=
=
⋅
=
−
−
2
2 10
1
3
1
36. 10 litara benzina ima masu (
ρ
=900 kgm
-3
):
A) 9 kg
B) 900 kg
C) 11,1 kg
D) 1,11 kg
E) 90 kg
rješenje:
(A)
V=10 l
ρ
=900 kgm
-3
m=?
m=V·
ρ
=10·10
-3
m
3
·900 kgm
-3
=9 kg
37. U teku
ć
inu gusto
ć
e 13,5·10
3
kgm
-3
uronjeno je homogeno tijelo gusto
ć
e 6,75·10
3
kgm
-3
.
Koji dio volumena tijela (u postocima) je iznad površine teku
ć
ine?
A) 100%
B) 50%
C) 20%
D) 10%
E) 2%
rješenje:
(B)
ρ
t
=13,5·10
3
kgm
-3
ρ
tj
=6,75·10
3
kgm
-3
G=U
V
tj
⋅ρ
tj
⋅
g=V
ur tj
⋅ρ
t
⋅
g
V
V
neur
tj
=
? %
V
V
kgm
kgm
V
V
ur tj
tj
tj
t
neur
tj
.
,
,
=
=
⋅
⋅
⋅
=
⇒
=
−
−
ρ
ρ
6 75 10
13 5 10
100
50%
50%
3
3
3
3
38. Amplituda harmoni
č
kog titranja je 2 cm, a frekvencija 0,5 s
-1
. Izraz koji opisuje ovo
titranje je:
A) y=(2 cm) sin (3,14 s
-1
)t
B) y=(2 cm) sin (6,24 s
-1
)t
C) y=(2 cm) sin (9,42 s
-1
)t
D) y=(4 cm) sin (3,14 s
-1
)t
E) y=(4 cm) sin (6,28 s
-1
)t
rješenje:
(A)
y
0
=2 cm
f=0,5 s
-1
y=?
y=y
0
sin
ω
t
y=(2 cm)sin (2
π
·0,5 s
-1
)·t
y=(2 cm)sin (3,14 s
-1
)·t

115
43. Težina tijela mase 100 kg je:
A) 0,098 N
B) 0,98 N
C) 9,8 N
D) 98 N
E) 980 N
rješenje:
(E)
m=100 kg
G=?
G=m·g=100
kg·9,8
ms
-2
=980 N
44. Izraz za snagu je:
A) mv
B) mv
2
/2
C) F·v
D) F·s
E) F·t
rješenje:
(C)
P
W
t
F s
t
Fv
=
⇒
⋅
⇒
45. U to
č
ki A tijela djeluje sila od 1 N, a u to
č
ki B njoj paralelna sila od 1/2 N. One se
mogu uravnotežiti silom od:
A) 1 N
B) 3 N
C) 2/3 N
D) 3/2 N
E) 1/3 N
rješenje:
(D)
F
1
=1 N
F
2
=1/2 N
R=?
r
r
r
R
F
F
N
N
N
1
1
2
1
1
2
3
2
=
+
=
+
=
46. U teku
ć
inu
č
ija je gusto
ć
a 13,5·10
3
kgm
-3
uronjeno je homogeno tijelo gusto
ć
e 9·10
3
kgm
-3
. Koji dio volumena tijela je iznad površine teku
ć
ine?
A) 1/4
B) 2/3
C) 1/2
D) 1/3
E) 1/4
rješenje:
(D)
ρ
t
=13,5·10
3
kgm
-3
ρ
tj
=9·10
3
kgm
-3
V
V
neur
tj
=
?
G=U
V
ur tj
⋅ρ
t
⋅
g= V
tj
⋅ρ
tj
⋅
g
V
V
ur
tj
tj
t
=
⋅ρ
ρ
116
V
= V - V
neur
tj
ur
V
V
V
V
neur
tj
tj
tj
t
tj
=
−
⋅ρ
ρ
:
V
V
kgm
kgm
neur
tj
tj
t
= −
= −
⋅
⋅
=
=
−
−
1
1
9 10
13 5 10
0 3333
1
3
3
3
3
3
ρ
ρ
,
,
47. Amplituda harmoni
č
nog titranja je 6 cm, a frekvencija 5 s
-1
. Izraz koji opisuje ovo titra-
nje je:
A) y=(6 cm) sin (31,4 s
-1
)·t
B) y=(6 cm) sin (62,8 s
-1
)t
C) y=(6 cm) sin (94,2 s
-1
)·t
D) y=(12 cm) sin (31,4 s
-1
)·t
E) y=(12 cm) sin (62,8 s
-1
)·t
rješenje:
(A)
y
0
=6 cm
f=5 s
-1
y=?
y=y
0
sin
ω
t
y=y
0
sin 2
π
f·t
y=(6 cm) sin (31,4 s
-1
)t
48. Kolika je duljina zvu
č
nog vala frekvencije 440 Hz, ako je brzina širenja 330 ms
-1
?
A) 0,75 m
B) 1,5 m
C) 0,5 m
D) 7,5 m
E) 1,33 m
rješenje:
(A)
f=440 Hz
v=330 ms
-1
λ
=?
λ = =
=
−
−
v
f
ms
s
m
330
440
0 75
1
1
,
49. Kroz potroša
ć
te
č
e struja od 5 mA kroz 1 minutu i 40 sekundi. Koliki je naboj prošao
potroša
č
em?
A) 5·10
-3
C
B) 5·10
-2
C
C) 5·10
-1
C
D) 7·10
-3
C
E) 7 C
rješenje:
(C)
I=5 mA
t=1 min 40 s
Q=?
Q=I·t
Q=5·10
-3
A·100 s
Q=5·10
-1
C

118
D) F·
Δ
t
E) m·v
rješenje:
(D)
55. Ako njihalo duljine L ima periodu 2s. Kolika je duljina njihala sa periodom 4s?
A) L/4
B) L/2
C) L
D) 2L
E) 4L
rješenje:
(E)
T
1
=2s
T
2
=4s
L
2
=?
T
T
L
g
L
g
T
T
L
L
L
L
T
T
L
s
s
L
2
1
2
1
2
2
1
2
2
1
2
1
2
2
1
2
1
2
2
1
2
2
16
4
4
=
=
⇒
=
=
=
π
π
56. Tlak na stijenke podmornice koja miruje na dubini od 50 m je (približno!):
A) 0,2 MPa
B) 0,5 MPa
C) 1 MPa
D) 2 MPa
E) 5 MPa
rješenje:
(B)
h=50 m
P=?
P=
ρ
·gh=1000 kgm
-3
·10 ms
-2
·50 m=0,5 MPa
57. Težina tijela volumena 50 cm
3
, o
č
itana na dinamometru je 2 N. Koju silu (u N) pokazu-
je dinamometar uronimo li cijelo tijelo u vodu? Približno!
A) 0,1
B) 0,5
C) 1,0
D) 1,2
E) 1,5
rješenje:
(E)
V=50 cm
3
G=2N
F=?
F=G-U=G-V
⋅ρ⋅
g=2N-50
⋅
10
-6
m
3
⋅
10
3
kgm
-3
⋅
10ms
-2
=2N-0,5N=1,5 N
58. Koliku koli
č
inu topline preda okolini 2 g željeza (c=500 Jkg
-1
K
-1
) ako se ohladi od
50
0
C na 10
0
C?
A) 40000 J
119
B) 323 J
C) 313 J
D) 313000 J
E) 40 J
rješenje:
(E)
m=2 g
c=500 Jkg
-1
K
-1
t
1
=50
0
C
t
2
=10
0
C
Q=?
Q=mc
Δ
t=2
⋅
10
-3
kg
⋅
500Jkg
-1
K
-1
⋅
40K=40J
59. Idealni plin je zatvoren u posudi stalnog volumena. Ako temperatura poraste od 0 °C na
273 °C, tlak:
A) ostaje nepromijenjen
B) poraste dva puta
C) poraste
č
etiri puta
D) poraste 136,5 puta
E) poraste 273 puta
rješenje:
(B)
V=konst.
t
1
=0 °C=273 K
t
2
=273 °C=546 K
P
T
P
T
1
1
2
2
=
(izohorna promjena stanja plina)
P
2
=?
P
P
T
T
P
K
K
P
2
1
1
2
1
1
546
273
2
=
⋅
=
⋅
=
60. Primarna zavojnica transformatora ima 200 zavoja, koliko zavoja ima sekundarna
zavojnica, ako je primarni napon 220 V, a sekundarni 55000 V
A) 100000
B) 50000
C) 10000
D) 5000
E) 500
rješenje:
(B)
N
1
=200
U
1
=220V
U
2
=55000 V
U
N
U
N
1
1
2
2
=
N
2
=?
N
U
N
U
V
V
2
2
1
1
55000
200
220
50000
=
⋅
=
⋅
=
61. Jedinica za otpornost je:
A)
Ω
B)
Ω
m
C)
Ω
m
2
D)
Ω
m
-1

121
E) 1,25 g
rješenje:
(D)
V=1 cm
3
ρ
=800 kgm
-3
m=?
m=V
⋅ρ
=10
-6
m
3
⋅
800kgm
-3
=8
⋅
10
-4
kg=0,8 g
65. Motor snage 50 W radi 5 dana. Koliki je rad izvršio?
A) 250 J
B) 600 J
C) 600 Wh
D) 6000 J
E) 6000 Wh
rješenje:
(E)
P=50 W
t=5 dana
W=?
W=P·t=50W·5·24
h=6000
Wh
66. Njihalo ima duljinu 1 m. Kolika je perioda? Približno!
A) 0,25 s
B) 0,5 s
C) 1,0 s
D) 2,0 s
E) 4,0 s
rješenje: (D)
l=1 m
T=?
T
l
g
m
ms
s
=
= ⋅
=
−
2
2 3 14
1
9 81
2 005
2
π
,
,
,
67. Valna duljina vala frekvencije 1 kHz je 1,2 m. Kolika je brzina širenja vala?
A) 1,2 ms
-1
B) 12 ms
-1
C) 120 ms
-1
D) 1200 ms
-1
E) 12000 ms
-1
rješenje:
(D)
f=1 kHz
λ
=1,2 m
v=?
v=
λ
·f=1,2m
⋅
10
3
s
-1
=1200 ms
-1
68. Koliku koli
č
inu topline treba dovesti bez gubitaka vodi temperature 20
0
C, mase 50 g da
se zagrije na 100
0
C? (c=4200 Jkg
-1
K
-1
)
A) 4200 kJ
B) 420 kJ
C) 21 kJ
D) 16,8 kJ
122
E) 4,2 kJ
rješenje:
(D)
t
1
=20
0
C
m=50 g
t
2
=100
0
C
Q=?
Q=m
⋅
c
⋅Δ
t=0,05 kg·4200 Jkg
-1
K
-1
·80 K=16800 J=16,8 kJ
69. Hidrostatskom tlaku od 100 kPa odgovara visina stupca vode od:
A) 1 m
B) 10 m
C) 100 m
D) 1 cm
E) 10 cm
rješenje:
(B)
P=100 kPa
h=?
P
g h
h
P
g
Pa
kgm
ms
m
= ⋅ ⋅
=
⋅
=
⋅
⋅
=
−
−
ρ
ρ
100 10
10
10
10
3
3
3
2
70. Idealni plin se rastegao izobarno zbog promjene temperature od -50
0
C do 173
0
C.
Volumen se pri tome pove
ć
ao:
A) dva puta
B) tri puta
C)
č
etri puta
D) 50 puta
E) 173 puta
rješenje:
(A)
t
1
=-50
0
C=223 K
t
2
=173
0
C=446 K
V
T
V
T
V
V
T
T
V
K
K
V
1
1
2
2
2
1
1
2
1
1
446
223
2
=
=
⋅
=
⋅
=
71. Me
đ
u polove magneta ulazi nabijena
č
estica po putanji okomitoj na smjer magnetskog
polja. Na nju djeluje sila:
A) u smjeru brzine
B) u smjeru suprotnom od smjera brzine
C) u smjeru magnetskog polja
D) u smjeru suprotnom smjeru magnetskog polja
E) u smjeru okomito na magnetsko polje
rješenje:
(E)
Pravilo desne ruke.

124
75. Koliko N iznosi sila kojom homogeno elektri
č
no polje jakosti 1 kNC
-1
djeluje na naboj
1 mC?
A) 10
3
B) 1
C) 10
-3
D) 10
6
E) 10
-6
rješenje:
(B)
E=1 kNC
-1
Q=1 mC
F=?
F=E·Q=1
⋅
10
3
NC
-1
⋅
10
-3
C=1 N
76. Zavojnica ima 5000 zavoja na duljini 50 cm. Kad kroz nju te
č
e struja 50 mA magnetsko
polje u njoj iznosi:
A) 500 Am
-1
B) 500 Am
C) 5 Am
-1
D) 125 Am
-1
E) 125000 Am
rješenje:
(A)
N=5000
l=50 cm
I=50 mA
H=?
H
N I
l
A
m
Am
= ⋅ =
⋅ ⋅
=
−
−
5000 50 10
0 5
500
3
1
,
77. Koliki se napon inducira u zavojnici s koeficijentom samoindukcije 20 mH ako je
brzina promjene struje u njoj 1,5 As
-1
?
A) 30 V
B) 3 V
C) 30 mV
D) 3 mV
E) 75 V
rješenje:(C)
L
mH
I
t
As
=
=
−
20
1 5
1
Δ
Δ
,
U = ?
U
L
I
t
= Δ
Δ
U = 20
⋅
10
-3
H
⋅
1,5As
-1
= 0,03V = 30 mV
78. Radioaktivni izvor nakon 60 sati ima 1/16 po
č
etnog broja jezgara. Njegovo vrijeme
poluraspada (u satima) je:
A) 60
B) 30
C) 15
D) 7,5
125
E) 3,75
rješenje:
(C)
t
sati
N
N
T
=
=
=
60
1
16
0
1
2
?
N
N
N
N
t
T
T
t
sati
sati
t
T
t
T
t
T
=
⋅
=
=
=
=
= =
=
−
−
−
−
0
0
4
2
2
2
1
16
2
4
4
60
4
15
1
2
1
2
1
2
1
2
1
2
79. Ura njihalica prenesena s zemaljskog ekvatora na sjeverni pol:
A) ide brže
B) ne pokazuje promjene
C) smanjuje periodu njihanja
D) ide sporije
E) mijenja veli
č
inu amplitude
rješenje:
(A)
T
l
g
=
2
π
g je ve
ć
a na polu nego na ekvatoru, što zna
č
i da
ć
e T na polu biti manje, te ura ide brže.
80. Kuglica se po
č
ne kotrljati niz kosinu i prije
đ
e put od 10 cm u 1 s. Ubrzanje kuglice
izraženo u cm/s
2
iznosi:
A) 2
B) 20
C) 4
D) 40
E) 10
rješenje:
(B)
s=10 cm
t=1 s
a=?
s
a t
a
s
t
cm
s
cms
= ⋅
=
= ⋅
=
−
2
2
2
2
2
2
2 10
1
20
81. Jednoliko gibanje po kružnici spada u:
A) jednoliko gibanje s obzirom na vektor brzine

127
v
1
=0
s=20 m
v
=?
v
gs
ms
m
ms
v
v
v
ms
ms
=
=
⋅
⋅
=
=
+
=
+
=
−
−
−
−
2
2 10
20
20
2
0
20
2
10
2
1
1
1
1
(
)
85. Tijelo pliva na teku
ć
ini tako da mu je 4/5 volumena pod površinom. Odnos gusto
ć
e
tijela i gusto
ć
e teku
ć
ine je:
A) 0,8
B) 1,25
C) 4,5
D) 5,4
E) 1,2
rješenje:
(A)
V
ur
=4/5V
tj
ρ
ρ
tj
t
=
?
G
U
V
g
V
g
V
V
V
V
tj
tj
ur
t
tj
t
ur
tj
tj
tj
=
⋅
⋅ =
⋅ ⋅
=
=
=
ρ
ρ
ρ
ρ
4
5
0 8
,
86. Ako jedno titranje kasni T/4 za drugim titranjem iste frekvencije razlika u fazi titranja
je:
A) 45
0
B) 90
0
C) 120
0
D) 240
0
E) 360
0
rješenje:
(B)
T
→
360
0
T/4
→
90
0
Tijekom perioda (T) tijelo opiše puni kut od 360
0
, te
ć
e za T/4 opisati
č
etvrtinu punog kuta,
tj. 90
0
.
87. Pri prijelazu iz jednog sredstva u drugo val:
A) ne mijenja smjer
B) mijenja valnu duljinu i frekvenciju
C) ne mijenja valnu duljinu
D) ne mijenja frekvenciju
E) mijenja frekvenciju
rješenje:
(D)
88. Nosioci elektri
č
ne struje u bakru su:
A) negativni ioni bakra
B) atomi bakra
C) pokretni ioni bakra
D) elektroni
128
E) pozitivni ioni bakra
rješenje:
(D)
89. Na opti
č
ku rešetku pada okomito žuto i plavo monokromatsko svjetlo. Kut prvog ogib-
nog maksimuma je:
A) jednak za obje valne duljine
B) ve
ć
i za žuto svjetlo
C) ve
ć
i za plavo svjetlo
D) proporcionalan razlici valnih duljina
E) proporcionalan sumi valnih duljina
rješenje:
(B)
90. Kroz presjek nekog vodi
č
a u 0,5 min pro
đ
e naboj od 180 C. Srednja jakost struje izra-
žena u amperima je:
A 360
B) 180
C) 90
D) 6
E) 0,5
rješenje: (D)
t=0,5 min=30 s
Q=180 C
I=?
I
Q
t
C
s
A
=
=
=
180
30
6
91. Na naboj od 500 mC djeluje sila od 5 N. Elektri
č
no polje izraženo u N/C iznosi:
A) 0,01
B) 0,1
C) 1
D) 10
E) 100
rješenje:
(D)
Q=500 mC
F=5 N
E=?
E
F
Q
N
C
NC
=
=
⋅
=
−
−
5
500 10
10
3
1
92. Vodi
č
otpora 1
Ω
, dužine 1 m i presjeka 1 mm
2
ima elektri
č
nu otpornost (izraženu u
Ω
m):
A) 1
B) 10
3
C) 10
-3
D) 10
6
E)10
-6
rješenje:
(E)

130
d
mm
k
m
=
=
=
=
1
100
1
2
λ
μ
α
sin
?
k
d
k
d
m
m
⋅ = ⋅
= ⋅ = ⋅ ⋅
=
−
−
λ
α
α
λ
sin
sin
,
1 2 10
10
0 2
6
5
97. Neispravan izraz za centripetalno ubrzanje je:
A) v
2
R
-1
B) 4
π
2
f
2
R
2
C) 4
π
2
Rf
2
D) 4
π
2
R/T
2
E) (2v)
2
/4R
rješenje:
(B)
98. Sila uzgona (u N) koja djeluje na kocku (dužina brida 10 cm) od željeza (gusto
ć
a 7000
kg/m
3
uronjenu u vodu (gusto
ć
a 1000 kg/m
3
) je (uzeti g=10m/s
2
)
A) 0,01
B) 0,1
C) 1
D) 10
E) 100
rješenje:
(D)
a=10 cm
ρ
=700 kg/m
3
ρ
t
=1000 kg/m
3
U=?
U=V
⋅ρ
t
⋅
g=a
3
⋅ρ
t
⋅
g=0,1
3
m
3
⋅
1000kgm
-3
⋅
10ms
-2
=10 N
99. Hidrostatski tlak u vodi (gusto
ć
a 1000 kg/m
3
) na dubini od 1 cm ispod površine iznosi
(tlak je izražen u kPa, a za g uzeti 10 m/s
2
)
A) 0,1
B) 10
C) 1
D) 100
E) 1000
rješenje:
(A)
ρ
=1000 kg/m
3
h=1 cm
P=?
P=
ρ⋅
g
⋅
h=1000 kg/m
-3
·10 ms
-2
·10
-2
m=100 Pa=0,1 kPa
100. Efektivni napon gradske mreže je:
A) srednja vrijednost izmjeni
č
nog napona
B) maksimalna vrijednost izmjeni
č
nog napona
C) napon koji je, približno, 30% manji od 310 V
131
D) napon koji je, približno, 70% manji od 310 V
E) jednak 310 V
rješenje:
(C)
U
U
U
U
ef
=
=
=
0
0
0
2
0 70
70%
,
101. Dva tijela istog oblika a razli
č
itih masa kližu niz kosinu. Uz pretpostavku da je trenje
zanemarivo, tijela
ć
e se gibati:
A) jednoliko s jednakim brzinama
B) jednoliko ubrzano s jednakim akceleracijama
C) jednoliko ubrzano, a ve
ć
u akceleraciju
ć
e imati tijelo manje mase
D) jednoliko ubrzano, a ve
ć
u akceleraciju
ć
e imati tijelo ve
ć
e mase
E) jednoliko, ali s razli
č
itim brzinama
rješenje:
(B)
102. Koliki je period gramofonske plo
č
e koja napravi 45 okretaja u minuti?
A) 1,333 s
B) 0,016 s
C) 0,022 s
D) 0,750 s
E) 1,000 s
rješenje:
(A)
f=45 min
-1
T=?
T
f
s
s
= =
=
=
−
1
1
45
60
45
1 333
1
min
,
103. Ophodno vrijeme tijela koje se giba jednoliko po kružnici:
A) upravno je razmjerno s ophodnom brzinom
B) obrnuto je razmjerno s ophodnom brzinom
C) ne ovisi o ophodnoj brzini
D) upravno je razmjerno s masom tijela
E) obrnuto je razmjerno s masom tijela
rješenje:
(B)
104. Koliko je visok stupac alkohola gusto
ć
e 800 kgm
-3
koji drži ravnotežu stupcu vode od
240 mm gusto
ć
e 1000 kgm
-3
?
A) 0,300 m
B) 0,200 m
C) 0,192 m
D) 3,000 m
E) 1,920 m
rješenje:
(A)
ρ
1
=800 kgm
-3
ρ
2
=1000 kgm
-3
h
2
=240 mm
h
1
=?
p
p
g h
g h
1
2
1
1
2
2
=
⋅ ⋅
=
⋅ ⋅
ρ
ρ

133
B) 9,81 kg
C) 98,1 kg
D) 100 kg
E) 10 kg
rješenje:
(D)
G=981 N
m=?
G
mg
m
G
g
N
ms
kg
=
=
=
=
−
981
9 81
100
2
,
109. Tijelo mase 6 kg nalazi se 12 m iznad tla. Na kojoj visini u metrima treba biti tije-lo
mase 18 kg da bi oba imala istu potencijalnu energiju?
A) 12
B) 4
C) 6
D) 9
E) 3
rješenje:
(B)
m
1
=6 kg
h
1
=12 m
m
2
=18 kg
h
2
=?
Ep
Ep
m gh
m gh
h
m h
m
kg
m
kg
m
1
2
1
1
2
2
2
1 1
2
6
12
18
4
=
=
=
=
⋅
=
110. Dva se tijela gibaju jednoliko svako po svojoj kružnici, a pri tome imaju jednake
centripetalne akceleracije. Ako za radijuse njihovih putanja vrijedi r
1
:r
2
=4:1, onda za
njihove ophodne brzine vrijedi:
A) v
1
:v
2
=4:1
B) v
1
:v
2
=2:1
C) v
1
:v
2
=1:1
D) v
2
:v
1
=2:1
E) v
2
:v
1
=4:1
rješenje:(B)
r
1
:r
2
=4:1
a
1
=a
2
v
1
:v
2
=?
F
mv
R
a
v
R
a
a
v
R
v
R
v
v
R
R
v
v
R
R
c
=
⇒
=
=
=
=
=
=
=
2
2
1
2
1
2
1
2
2
2
1
2
2
2
1
2
1
2
1
2
4
1
21
:
134
111. Na kojoj dubini u vodi gusto
ć
e 1000 kgm
-3
je tlak 1,5 bar? (atmosferski tlak neka je 1
bar, a g=10 ms
-2
)
A) 15 m
B) 50 m
C) 0,5 m
D) 5 m
E) 1,5 m
rješenje:
(D)
ρ
=1000 kgm
-3
P=1,5 bar
P
a
=1 bar
h=?
P
g h
P
h
P
P
g
bar
bar
kgm
ms
Pa
kgm
s
m
a
a
= ⋅ ⋅ +
=
−
⋅
=
−
⋅
=
⋅
=
−
−
− −
ρ
ρ
1 5
1
1000
10
0 5 10
10
5
3
2
5
4
2
2
,
,
112. Koliku koli
č
inu topline (u kJ) preda okolini 10 kg vode ako se ona ohladi sa 30
0
C na
20
0
C (c=4180 Jkg
-1
K
-1
)
A) 4,18
B) 418
C) 418000
D) 209
E) 209000
rješenje:
(B)
m=10 kg
t
1
=30
0
C
t
2
=20
0
C
Q=?
Q=m
⋅
c
⋅Δ
t=10kg·4180 Jkg
-1
K
-1
·10K=418000J=418 kJ
113. Volumen plina u posudi je 9 litara, a tlak 5·10
4
Pa. Ako se bez promjene temperature,
volumen plina smanji za 3 litre tlak je:
A) 7,5·10
4
Pa
B) 2,5·10
4
Pa
C) 15·10
4
Pa
D) 10·10
4
Pa
E) 1,7·10
4
Pa
rješenje:
(A)
V
1
=9 l
P
1
=5·10
4
Pa
V
2
=6 l
P
2
=?
P V
P V
P
P V
V
Pa
l
l
Pa
1
1
2
2
2
1
1
2
4
4
5 10
9
6
7 5 10
=
=
= ⋅
⋅ = ⋅
,
114. Kad se struja promijeni brzinom 2 As
-1
u zavojnici se zbog samoindukcije inducira
napon od 0.04 V. Koeficijent samoindukcije te zavojnice je u henrijima:
A) 0,02
B) 0,08
C) 0,01
D) 0,32

136
rješenje: (C)
T
l
g
=
2
π
Ako ura njihalica kasni, zna
č
i da je period titranja preduga
č
ak, a on
ć
e se smanjiti skra
ć
iva-
njem dužine njihala.
118. U to
č
ki elektri
č
nog polja veli
č
ine 2 N/C nalazi se naboj od 6 C. Sila elektri
č
nog polja
na naboj je:
A) 2 N
B) 3 N
C) 6 N
D) 12 N
E) 6/2 N
rješenje:
(D)
E=2 N/C
Q=6 C
F=?
F=Q
⋅
E=6C
⋅
2N/C=12 N
119. Tijelo prevali put od 3 km za 15 minuta. Srednja brzina tijela u km/h je:
A) 0,2
B) 200
C) 1,2
D) 12
E) 120
rješenje:
(D)
s=3 km
t=15 min
v
=?
v
s
t
km
h
km h
= =
=
3
15
60
12
/
120. Motor podigne teret mase 50 kg za 2 minute 6 metara visoko. Kolika je snaga motora?
A) 150 W
B) 1500 W
C) 2,5 W
D) 25 W
E) 250 W
rješenje:
(D)
m=50 kg
t=2 min
h=6 m
P=?
P
W
t
m g h
t
kg
ms
m
s
W
=
=
⋅ ⋅ =
⋅
⋅
⋅
=
−
50
10
6
2 60
25
2
121. Žarulja snage 100 W gorjela je 30 minuta. Koliko je elektri
č
ne energije u kWh
utrošila?
A) 3000
137
B) 50
C) 8
D) 0,05
E) 0,005
rješenje:
(D)
P=100 W
t=30 min
W=?
W=P
⋅
t=100W
⋅
0,5h=50Wh=0,05 kWh
122. Žica duljine 1 m, presjeka 0,2 mm
2
ima otpor 2,5 oma. Kolika je otpornost, u om
metrima, materijala iz kojeg je žica izra
đ
ena?
A) 0,5·10
-9
B) 0,5·10
-6
C) 0,5·10
-4
D) 0,5·10
-2
E) 0,5
rješenje
(B)
l=1 m
S=0,2 mm
2
R=2,5
Ω
ρ
=?
R
l
S
R S
l
m
m
m
=
⋅
= ⋅ =
⋅
⋅
=
⋅
−
−
ρ
ρ
2 5
0 2 10
1
0 5 10
6
2
6
,
,
,
Ω
Ω
123. Zavojnicu u titrajnom krugu zamijenimo zavojnicom sa 9 puta ve
ć
im koeficijentom
samoindukcije. Uz nepromijenjeni kondenzator, frekvencija titrajnog kruga je sada:
A) 9 puta ve
ć
a
B) 6 puta ve
ć
a
C) 3 puta ve
ć
a
D) 3 puta manja
E) 9 puta manja
rješenje:
(D)
L
2
=9L
1
f
1
:f
2
=?
f
f
L C
L C
f
f
f
f
1
2
1
1
1
1
1
2
2
1
1
2
1
2
9
3
1
1
3
=
⇒
=
⇒
=
π
π
124. Razlaganje bijele svjetlosti na boje prolazom kroz opti
č
ku mrežicu zove se:
A) disperzija
B) difrakcija
C) polarizacija
D) fotoefekt
E) interferencija

139
128. Kad se brzina nekog tijela pove
ć
a 3 puta, tada se 3 puta pove
ć
a i:
A) njegova akceleracija
B) ukupna energija tog tijela
C) potencijalna energija tijela
D) koli
č
ina gibanja tijela
E) kineti
č
ka energija tijela
rješenje:
(D)
koli
č
ina gibanja=m
⋅Δ⋅
v
129. Klip ima površinu 0,5 dm
2
i zatvara posudu s teku
ć
inom. Ako je u teku
ć
ini hidrauli
č
ki
tlak 10
6
Pa, kolika je sila koja djeluje na klip?
A) 5000 N
B) 5·10
5
N
C) 2·10
5
N
D) 2000 N
E) 2·10
4
N
rješenje:(A)
S=0,5 dm
2
P=10
6
Pa
F=?
P
F
S
F
P S
Pa
m
N
=
= ⋅ =
⋅
⋅
=
−
10
0 5 10
5000
6
2
2
,
130. Nekoliko tijela razli
č
itih masa, gusto
ć
a i oblika ubacimo u vodu Na vodi
ć
e plivati ona
tijela koja imaju:
A) pravilan geometrijski oblik
B) malu masu
C) gusto
ć
u kao i voda
D) gusto
ć
u ve
ć
u od vode
E) gusto
ć
u manju od vode
rješenje:
(E)
ρ
tijela
=
ρ
tek.
- tijelo pluta
ρ
tijela
>
ρ
tek.
- tijelo tone
ρ
tijela
<
ρ
tek.
- tijelo pliva
131. Tijelu mase 1 kg temperatura poraste za 1
0
C. Kolika je promjena unutarnje energije
toga tijela kada se zna da je specifi
č
ni toplinski kapacitet 120 Jkg
-1
K
-1
?
A) 1 J
B) 0 J
C) 120 J
D) 120 kJ
E) 8 mJ
rješenje:
(C)
m=1 kg
Δ
t=1
°
C=1 K
C=120 Jkg
-1
K
-1
Δ
U=?
Δ
Δ
Δ
U
Q
U
mc t
kg
Jkg
K
K
J
=
=
=
⋅
⋅
=
−
−
1
120
1
120
1
1
140
132. Kondenzator kapaciteta C izbija se kroz uzvojnicu uz frekvenciju f. Ako se kapacitet
kondenzatora u
č
etverostru
č
i frekvencija titrajnog kruga bit
ć
e:
A) f/4
B) f/2
C) 2f
D) 4f
E) f
rješenje:
(B)
C
2
=4C
1
f
2
=?
f
L C
f
L
C
L C
f
f
1
1
1
2
1
1
1
1
1
1
1
2
1
2
4
1
2
1
2
1
2
2
=
=
= ⋅
=
=
π
π
π
133. Energija fotona vidljive svjetlosti:
A) raste s pove
ć
anjem valne duljine
B) obrnuto je razmjerna valnoj duljini
C) dana je omjerom frekvencije i valne duljine
D) dana je umnoškom Planckove konstante i valne duljine
E) obrnuto je razmjerna frekvenciji
rješenje: (B)
E
h c
= ⋅
λ
134. Tesla je jedinica za:
A) permeabilnost tvari
B) veli
č
inu magnetskog polja
C) gusto
ć
u magnetskog polja
D) magnetski tok
E) gusto
ć
u permeabilnosti
rješenje:
(C)
135. Za vrijeme jedne periode elongacija harmonijskog titranja jednaka je nuli:
A) dva puta
B) jedan put
C) 2 puta
D) tri puta
E) 2
2
puta
rješenje:
(A)
136. Brewsterov zakon glasi (
α
je upadni kut,
β
je kut loma a n indeks loma tvari)
A) tg(
α
+
β
)=n
B) cos
α
/sin
α
=n
C) tg(
α
-
β
)=n

142
C) 20
D) 25
E) 30
rješenje:
(E)
h=45 m
v=?
v
gh
ms
m
ms
=
=
⋅
⋅
=
−
−
2
2 10
45
30
2
1
141. Na tijelo je kroz 2 stotinke sekunde djelovala sila od 150 N. Kolika je promjena
koli
č
ine gibanja tijela?
A) 300 kgms
-1
B) 3 kgms
-1
C) 75 Ns
-1
D) 7500 kgms
-1
E) 0
rješenje:
(B)
Δ
t=2·10
-2
s
F=150N
Δ
(m·v)=?
Δ
(m·v)=F
⋅Δ
t=150N
⋅
2
⋅
10
-2
s=3Ns=3kgms
-2
s=3 kgms
-1
142. Tijelo u prirodi slobodno pada. Kroz kratki vremenski period na njega djeluje dodatna
sila suprotnog smjera od sile teže. Akceleracija tijela nakon prestanka djelo-vanja te sile:
A) manja je od akceleracije slobodnog pada
B) ve
ć
a je od g
C) jednaka je 0
D) jednaka je g
E) iznosi g/2
rješenje:
(D)
143. Od metala gusto
ć
e 3000 kgm
-3
izrezana je kocka. Brid kocke je 30 cm. Koliko
kilogarama ima kocka?
A) 8,1
B) 81
C) 810
D) 8100
E) 0,810
rješenje: (B)
ρ
=3000 kgm
-3
a=30 cm=0,3 m
m=?
m=
ρ
·V=3000 kgm
-3
⋅
(0,3 m)
3
=81 kg
144. Ravni val prelazi iz jedne sredine u drugu u kojoj je brzina širenja manja, a na granicu
pada okomito. Pri prijelazu dolazi do:
A) pove
ć
anja frekvencije
B) smanjenja frekvencije
C) promjene smjera širenja
D) pove
ć
anja valne duljine
143
E) smanjenja valne duljine
rješenje:
(E)
145. Grafi
č
ki prikaz Charlesovog zakona u pravokutnom koordinatnom sustavu je pravac.
Taj pravac presijeca temperaturnu os na:
A)+4
0
C
B) -4
0
C
C) 0
0
C
D)+100
0
C
E) -273
0
C
rješenje:
(E)
Izohorna promjena stanja plina: (V=konst).
Charlesov zakon: p=p
0
(1+
α
t).
Ako je p=0 onda je 0=p
0
(1+
α
t)
⇒
α
t=-1
t=-1/
α
t=-273,15
°
C
146. Rendgenske zrake imaju valnu duljinu 0,15 nm, a vidljiva svjetlost 0,45
μ
m. Energija
fotona rendgenskih zraka prema energiji fotona vidljive svjetlosti je:
A) 3000 puta ve
ć
a
B) 3000 puta manja
C) 300 puta ve
ć
a
D) 3 puta je ve
ć
a
E) jednaka je energiji fotona vidljive svjetlosti
rješenje:
(A)
λ
1
=0,15 nm
λ
2
=0,45
μ
m
E
1
/E
2
=?
E
E
h c
h c
m
m
E
E
1
2
1
2
2
1
6
9
1
2
0 45 10
0 15 10
3000
1
3000
=
⋅
⋅
=
=
⋅
⋅
=
=
−
−
λ
λ
λ
λ
,
,
147. Kolika je, približno, grani
č
na energija fotona (u J) koja uzrokuje fotoelektri
č
ni efekt
na metalu ako tome fotonu odgovara valna duljina od 400 nm (h=6,6·10
-34
Js)
A) 2,4·10
19
B) 2,4·10
-19
C) 5·10
-19
D) 6·10
-34
E) 6·10
34
rješenje:
(C)
λ
=400 nm
E=?
E
h c
Js
ms
m
J
= ⋅ =
⋅
⋅ ⋅
⋅
=
⋅
−
−
−
−
λ
6 6 10
3 10
400 10
4 95 10
34
8
1
9
19
,
,

145
A) 10
-6
B) 10
-9
C) 10
-15
D) 10
-12
E) 10
-14
rješenje:
(E)
10 fm=10·10
-15
m=10
-14
m
152. Prosje
č
ana gusto
ć
a drvene grede je 600 kgm
-3
, a gosto
ć
a vode 1000 kgm
-3
. Kad greda
pliva u vodi, koliki dio njezinog volumena viri iz vode?
A) 2/3
B) 2/5
C) 1/5
D) 3/5
E) 1/3
rješenje:
(B)
ρ
tj
=600 kgm
-3
ρ
t
=1000 kgm
-3
V
neur
=?
V
g
V
g
V
V
V
kgm
kgm
V
V
V
V
V
V
tj
tj
ur
tek
ur
tj
tj
tek
tj
tj
tj
neur
tj
tj
tj
⋅
⋅ =
⋅
⋅
=
⋅
=
⋅
=
=
=
−
=
−
−
ρ
ρ
ρ
ρ
600
1000
0 6
3
5
3
5
2
5
3
3
,
153. Kojom se brzinom u ms
-1
širi zvuk u željezu, ako ton frekvencije 1 kHz ima u željezu
valnu duljinu 5 m?
A) 200
B) 2000
C) 20
D) 500
E) 5000
rješenje:
(E)
f=1 kHz
λ
=5 m
v=?
v=
λ
·f=5m·1·10
3
Hz=5000 ms
-1
154. Pritisak plina u posudi iznosi 6·10
6
Pa na sobnoj temperaturi. Kad se ona spoji s
praznom posudom dva puta ve
ć
eg volumena, a temperatura ostane ista, tlak u obje posude
bit
ć
e:
A) 2·10
6
Pa
B) 3·10
6
Pa
C) 1,2·10
7
Pa
D) 1,8·10
7
Pa
E) 2·10
5
Pa
rješenje:
(A)
146
P
1
=6·10
6
Pa
V
2
=V
1
+2V
1
=3V
1
t=konst.
P
2
=?
P V
P V
P
P V
V
Pa V
V
Pa
1 1
2
2
2
1 1
2
6
1
1
6
6 10
3
2 10
=
=
=
⋅
⋅
= ⋅
155. Dva vodi
č
a imaju jednaku duljinu i jednake popre
č
ne presjeke, a od razli
č
itih su
materijala. Elektri
č
na otpornost jednog od njih je 0,1·10
-6
ommetra i otpor 10 oma. Koliki
je otpor u omima drugoga, ako je njegova otpornost 0,02·10
-6
ommetra.
A) 2
B) 0,5
C) 20
D) 50
E) 5
rješenje:
(A)
l
1
=l
2
s
1
=s
2
ρ
1
=0,1·10
-6
Ω
m
R
1
=10
Ω
ρ
2
=0,02·10
-6
Ω
m
R
2
=?
R
l
S
l
S
R
l
S
l
S
R
R
m
m
1
1
1
1
1
1
1
1
1
1
2
2
2
2
1
1
6
6
0 02 10
10
0 1 10
2
=
⋅
=
=
⇒
=
⋅
=
⋅
⋅
⋅
=
−
−
ρ
ρ
ρ
ρ
,
,
Ω
Ω
Ω
Ω
156. Frekvencija titrajnog kruga je 100 kHz. Koliki je period titranja u mikrosekundama?
A) 10
B) 100
C) 1000
D) 0,1
E) 0,01
rješenje:
(A)
f=100 kHz
T=?
μ
s
T
f
s
s
s
s
= =
⋅
=
= ⋅
=
−
−
−
1
1
100 10
10
10 10
10
3
1
5
6
μ
157. Kondenzator ima kapacitet 100 pF. Kolika koli
č
ina naboja u kulonima daje na njemu
napon 100 V?
A) 1
B) 10
8
C) 10
4
D) 10
-8
E) 10
-2
rješenje:
(D)
C=100 pF
U=100 V
Q=?
C
Q
U
Q
C U
F
V
C
=
= ⋅ =
⋅
⋅
=
−
−
100 10
100
10
12
8

148
D) 100
E) 0,1
rješenje:
(A)
h=100 mm
P=1 kPa
ρ
=?
P
g h
P
g h
Pa
ms
m
kgm
= ⋅ ⋅
=
⋅
=
⋅
⋅
=
−
−
ρ
ρ
1 10
10
0 1
1000
3
2
3
,
162. Ravnom valu, kad prelazi iz jednog sredstva u drugo u kojem
ć
e imati ve
ć
u brzi-nu:
A) smjer prostiranja ne
ć
e se promijeniti
B) porasti
ć
e frekvencija
C) smanjit
ć
e se frekvencija
D) pove
ć
at
ć
e se valna duljina
E) smanjit
ć
e se valna duljina
rješenje: (D)
v=
λ
·f
Frekvencija ostaje nepromijenjena, pa je nužno da se uz porast brzine pove
ć
ava i val-na
duljina.
163. Molekule razli
č
itih plinova na istoj temperaturi imaju jednaku:
A) brzinu
B) kineti
č
ku energiju
C) potencijalnu energiju
D) koli
č
inu gibanja
E) ukupnu energiju
rješenje:
(B)
T
N
R
E
A
k
= ⋅
⋅
2
3
N
A
=Avogadrova konstanta
R=plinska konstanta
164. Dva su svitka bakrene žice. Jedan sa žicom popre
č
nog presjeka 1 mm
2
, a drugi sa
žicom presjeka 0,25 mm
2
. Ako za otpornik uzmemo 4 m žice s presjekom 1 mm
2
, koliko bi
trebalo uzeti one druge da oba otpornika imaju jednake otpore?
A) 1 m
B) 4 m
C) 2 m
D) 1/2 m
E) 1/8 m
rješenje:
(A)
S
1
=1 mm
2
S
2
=0,25 mm
2
l
1
=4 m
ρ
1
=
ρ
2
R
1
=R
2
l
2
=?
R
R
l
S
l
S
l
l
S
S
m
mm
mm
m
2
1
2
2
1
1
2
1
2
1
2
2
4
0 25
1
1
=
⋅
=
⋅
=
⋅
=
⋅
=
ρ
ρ
,
149
165. Nukleoni su:
A) pozitroni i elektroni
B) pozitroni i neutroni
C) protoni i neutroni
D) elektroni i neutroni
E) elektroni i protoni
rješenje:
(C)
166. Energija vezanja po nukleonu za neku jezgru koja ima redni broj Z i maseni broj A
iznosi 7 MeV. Ukupna energija vezanja jezgre E/MeV je:
A) 7 A
B) 7 Z
C) 7 (A+Z)
D) 7 (A-Z)
E) 7 AZ
rješenje:
(A)
167. Tijelo mase 0,2 kg klizi bez trenja niz kosinu i prije
đ
e visinsku razliku od 10 m. Ako
je po
č
etna brzina 0 ms
-1
, kolika je kineti
č
ka energija na kraju puta?
A) 0,2 J
B) 1,96 J
C) 19,62 J
D) 2 J
E) 0,2 kJ
rješenje:
(C)
m=0,2 kg
Δ
h=10 m
E
k
=?
E
k
=
Δ
Ep=mg
Δ
h=0,2kg·9,81 ms
-2
·10 m=19,62 J
168. Plin se nalazi u posudi volumena 9 litara pod tlakom 5·10
4
Pa. Ako se bez promjene
temperature smanji volumen plina za 3 litre koliki
ć
e tada biti tlak?
A) 7,5·10
4
Pa
B) 2,5·10
4
Pa
C) 15·10
4
Pa
D) 10·10
4
Pa
E) 1,7·10
4
Pa
rješenje:
(A)
V
1
=9 l
P
1
=5·10
4
Pa
t=konst
V
2
=6 l
P
2
=?
P V
P V
P
P V
V
Pa
l
l
Pa
1
1
2
2
2
1
1
2
4
4
5 10
9
6
7 5 10
=
=
= ⋅
⋅ = ⋅
,
169. Kolika je valna duljina monokromske svjetlosti koja pada na opti
č
ku mrežicu s
konstantom 1800 nm, a sinus kuta ogibnog spektra tre
ć
eg reda je jedan?

151
s=400 km
s
1
=150 km
v
1
=120 km/h
s
2
=250 km
v=80 km/h
v
2
=?
t
s
v
km
km h
h
t
s
v
km
km h
h
t
t
t
h
h
h
v
s
t
km
h
km h
km h
= =
=
=
=
=
= − =
−
=
=
=
=
=
400
80
5
150
120
5
4
5
5
4
15
4
250
15
4
66 66
67
1
1
1
2
1
2
2
2
/
/
,
/
/
173. Puška se nalazi 2,5 m iznad tla. Kojom brzinom treba ispaliti tane da bi palo na zemlju
na udaljenosi od 300 m?
A) 450 m/s
B) 300 m/s
C) 350 m/s
D) 420 m/s
E) 280 m/s
rješenje:
(D)
h=2,5 m
D=300 m
v
0X
=?
D
v
h
g
v
D
h
g
m
m
ms
ms
ox
ox
=
⋅
=
=
⋅
=
−
−
2
2
300
2 2 5
9 81
420 2
2
1
,
,
,
174. Kružna plo
č
a promjera 7 m zakrene se za 90° u 2 sekunde. Kolika je obodna brzina?
A) 7,35 m/s
B) 5,50 m/s
C) 15,8 m/s
D) 2,75 m/s
E) 1,40 m/s
rješenje:
(D)
2R=7 m
f=1/4 okr/2 s
v=?
v
R
s
m
s
ms
=
⋅
=
⋅
⋅
=
−
2
1
4
2
7
3 14 0 25
2
2 75
1
π
,
,
,
175. Dvije kugle zagrijane na 100 °C, jedna od aluminija, a druga od olova predaju okolini
jednake koli
č
ine topline. Koliki je omjer volumena V
Al
:V
Pb
, ako se kugle ohlade na istu
temperaturu? (
ρ
Al
=2700 kg/m
3
;
ρ
Pb
=11340 kg/m
3
; c
Al
=880 J/kgK; c
Pb
=120 J/kgK)
A) 1,75
B) 0,57
C) 0,88
152
D) 1,20
E) 0,27
rješenje:
(B)
t=100 °C
Δ
t
1
=
Δ
t
2
Q
1
=Q
2
V
Al
:V
Pb
=?
Q
Q
m c
t
m c
t
V c
V c
V
V
c
c
kgm
JK
kg
kgm
JK
kg
Al
Al
Al
Pb
Pb
Pb
Al
Pb
Pb
Pb
Al
Al
1
2
1 1
2 2
3
1
1
3
1
1
11340
120
2700
880
0 572
=
=
=
=
=
⋅
⋅
=
−
−
−
−
−
−
Δ
Δ
ρ
ρ
ρ
ρ
,
176. Hidrauli
č
na preša ima
č
epove radijusa 20 cm i 45 cm. Kolika je sila na ve
ć
em
č
epu,
ako na manji djelujemo silom od 15 N?
A) 45 N
B) 150 N
C) 760 N
D) 35 N
E) 76 N
rješenje:
(E)
R
1
=20 cm=0,2 m
R
2
=45 cm=0,45 m
F
1
=15 N
F
2
=?
F
S
F
S
F
F S
S
F R
R
F R
R
N
m
m
N
1
1
2
2
2
1
2
1
1
2
2
1
2
1
2
2
1
2
2
2
2
2
15
0 45
0 2
75 93
=
=
⋅
=
⋅
=
⋅
=
⋅
=
π
π
,
,
,
177. Neko tijelo je elektri
č
no negativno nabijeno:
A) ako ima više negativnog nego pozitivnog naboja
B) ako ima negativan, a ne pozitivan naboj
C) ako ima jednak broj pozitivnog i negativnog naboja
D) ako nema pozitivnog naboja
E) ako ima suvišak pozitivnog naboja
rješenje:
(A)
178. Ako kalij bombardiramo brzim elektronima nastat
ć
e jezgra:
19
40
1
0
K
e
x
+
→
−
.
A)
20
40
Ca
B)
18
40
Ar
C)
20
40
Ar
D)
17
35
Cl
E)
20
39
Ca
rješenje:
(B)
19
40
1
0
18
40
K
e
Ar
+
→
−

154
183. Na pozitron u elektri
č
nom polju djeluje sila F. Ako na isto mjesto stavimo alfa
č
esticu
sila
ć
e na nju biti:
A) 2F
B) F
C) 4F
D) F/2
E) F/4
rješenje:
(A)
F=Q·v·Bsin
α
F
≈
Q
Q
α
=2Q
e
F
α
=2F
e
184. Pješak i biciklist kre
ć
u istovremeno na put prema cilju udaljenom 20 km. Koliko dugo
ć
e biciklist
č
ekati pješaka na cilju, ako mu je srednja brzina pet puta ve
ć
a od brzine pješaka
koja iznosi 5 km/h?
A) 3,2 h
B) 2 h
C) 2,8 h
D) 1,5 h
E) 0,8 h
rješenje:
(A)
s=20 km
v
1
=5 km/h
v
2
=25 km/h
t
1
=?
t
2
=?
Δ
t=?
t
s
v
t
km
kmh
t
h
1
1
1
1
1
20
5
4
=
=
=
−
t
s
v
t
km
kmh
t
h
2
2
2
1
2
20
25
0 8
=
=
=
−
,
Δ
t=t
1
-t
2
Δ
t=4h-0,8h
Δ
t=3,2h
185. Akceleracija sile teže na sjevernom polu je za 0,2% ve
ć
a od one u Zagrebu (g=9,81
ms
-2
). Za koliko je tijelo mase 1700 g teže na polu nego u Zagrebu?
A) 3,4 N
B) 340 N
C) 333 mN
D) 170 mN
E) 17 mN
rješenje:
(C)
m=1700 g=1,7 kg
g
1
=9,81 ms
-2
g
2
=1,02g
1
G
1
=?
G
2
=?
Δ
G=?
G
1
=m·g
1
=1,7kg·9,81ms
-2
=16,677 N
G
2
=mg
2
=1,7kg·1,02·9,81ms
-2
=17,0105 N
Δ
G=G
2
-G1=17,0105 N-16,677 N=0,3335N=333mN
186. Kugla mase 1,5 kg giba se brzinom od 3 ms
-1
. Druga kugla mase 2 kg sustiže je
brzinom od 5 ms
-1
. Kolika je brzina kugala nakon centralnog sudara?
155
A) 2,5 m/s
B) 6,0 m/s
C) 3,5 m/s
D) 4,1 m/s
E) 10,2 m/s
rješenje:
(D)
m
1
=1,5 kg
v
1
=3 ms
-1
m
2
=2 kg
v
2
=5 ms
-1
v=?
m v
m v
m
m
v
v
m v
m v
m
m
kg
ms
kg
ms
kg
kg
ms
1 1
2
2
1
2
1 1
2
2
1
2
1
1
1
1 5
3
2
5
1 5
2
4 14
+
=
+
⋅
=
+
+
=
⋅
+
⋅
+
=
−
−
−
(
)
,
,
,
187. Koliki dio volumena drvenog
č
amca viri iz vode? Gusto
ć
a drveta je 770 kg/m
3
, a
morske vode 1030 kg/m
3
.
A) 25%
B) 1/3
C) 20%
D) 1/2
E) 75%
rješenje:
(A)
ρ
tj
=770 kgm
-3
ρ
tek
=1030 kgm
-3
V
neur
=?
G
U
V
g
V
g
V
V
kgm
kgm
V
V
V
V
V
V
V
V
V
V
V
V
tj
tj
ur
tek
ur
tj
tj
tek
tj
tj
neur
tj
ur
tj
tj
tj
neur
tj
tj
tj
=
⋅
⋅ =
⋅
⋅
=
⋅
=
⋅
=
=
−
=
−
=
=
⋅
=
−
−
ρ
ρ
ρ
ρ
770
1030
0 75
0 75
0 25
0 25
100
25%
3
3
,
,
,
,
188. Masa tijela koje harmoni
č
no titra s periodom od 8 s iznosi 5 kg. Kolika je konstanta k
harmoni
č
ne sile?
A) 0,3 N/m
B) 5,4 N/m
C) 3,08 N/m
D) 0,7 N/m
E) 8,2 N/m
rješenje:
(C)
T=8 s
m=5 kg
k=?
F
m
T
x
k
m
T
kg
s
N m
= −
⋅
=
= ⋅
⋅
=
4
4
4 3 14
5
8
3 08
2
2
2
2
2
2 2
π
π
,
,
/

157
C) 11,5 kg
D) 3,2 t
E) 760 kg
rješenje:
(B)
h=5 m
m=600 g=0,6 kg
t
1
=150 °C
t
2
=20 °C
m
2
=?
Q
Ep
m c
t
m
g h
m
m c
t
g h
kg
Jkg
K
K
ms
m
kg
=
⋅ ⋅
=
⋅ ⋅
=
⋅ ⋅
⋅
=
⋅
⋅
⋅
=
−
−
−
Δ
Δ
2
2
1
1
2
0 6
880
130
10 00
5
1372 8
,
,
,
193. Kolika mora biti duljina bakrene žice promjera 2 mm da ima isti otpor kao i 1 m nikle-
ne žice istog promjera? Otpornost bakra je 0,0175·10
-6
omm, a nikla 0,0724·10
-6
omm.
A) 4 cm
B) 16 m
C) 4 m
D) 2 m
E) 50 cm
rješenje:
(C)
2r
1
=2 mm
R
1
=R
2
l
2
=1 m
2r
2
=2 mm
l
1
=?
R
R
l
S
l
S
l
l
S
S
m
m
m
m
1
2
1
1
1
2
2
2
1
2
2
1
1
2
6
6
0 0724 10
1
0 0175 10
4 137
=
⋅
=
⋅
=
⋅ ⋅ /
⋅ /
=
⋅
⋅
⋅
=
−
−
ρ
ρ
ρ
ρ
,
,
,
Ω
Ω
194. Neptun 238 ima vrijeme poluživota 2 dana. Nakon 6 dana ostalo je još neraspadnuto
37,5·10
-6
g neptuna. Kolika je po
č
etna masa u mikrogramima?
A) 225
B) 300
C) 150
D) 100
E) 75
rješenje:
(B)
T
1/2
=2 dana
t=6 dana
N=37,5·10
-6
g
N
0
=?
N
N
N
N
N
g
g
t
T
t
T
=
⋅
=
=
= ⋅
⋅
=
−
−
−
0
0
6
2
2
8
8 37 5 10
300
1
2
1
2
,
μ
195. Voza
č
č
amca koji se kre
ć
e po jezeru brzinom od 35 km/h po
č
inje ko
č
iti na udaljenosti
20 m od obale. Kolika je akceleracija ako se
č
amac potpuno zaustavlja na 2 m od obale?
A) -2,3 m/s
2
B) -5,2 m/s
2
158
C) -0,5 m/s
2
D) -2,6 m/s
2
E) -3,3 m/s
2
rješenje:
(D)
v=35 km/h
s=20 m-2 m
a=?
v
a s
a
v
s
m
s
m
ms
=
⋅
=
=
⋅
⎛
⎝⎜
⎞
⎠⎟
⋅
=
−
2
2
35 1000
3600
2 18
2 62
2
2
2
,
196. Kojom brzinom bi se morala okretati Zemlja da tijelo na ekvatoru ne pritiš
ć
e površinu
Zemlje? (R=6370 km)
A) 8,0 km/s
B) 2,5 km/s
C) 6,3 km/s
D) 3,4 km/s
E) 5,7 km/s
rješenje:
(A)
R=6370 km
g=9,81 ms
-2
v=?
m g
m v
R
v
R g
v
m
ms
ms
km s
⋅ =
⋅
=
⋅
=
⋅
⋅
=
⋅
=
−
−
2
3
2
2
1
6370 10
9 81
79 05 10
7 9
,
,
,
/
197. Tijelo mase 5 g izvrši 80 titraja u sekundi. Kolika sila djeluje na tijelo kada mu je
elongacija 0,3 cm?
A) 5,7 N
B) 8,4 N
C) 2,6 N
D) 3,8 N
E) 4,6 N
rješenje:
(D)
m=5 g
f=80 s
-1
x=0,3 cm
F=?
F
m x
T
F
m x f
kg
m
s
F
N
= −
⋅
=
⋅ ⋅
= ⋅
⋅ ⋅
⋅
⋅
⋅
=
−
−
−
4
4
4 3 14
5 10
0 3 10
80
3 786
2
2
2
2
2
3
2
2
2
π
π
,
,
,
198. Na kojoj temperaturi 25 molova nekog plina tla
č
i posudu od 0,4 m
3
tlakom 5·10
5
Pa?
(R=8,31 J/Kmol)
A) 690 °C
B) 730 °C

160
E) 1600 nm
rješenje:
(C)
k=2
sin
α
=0,5
λ
=800 nm
d=?
k
d
d
k
nm
nm
m
⋅ = ⋅
= ⋅ = ⋅
=
=
λ
α
λ
α
μ
sin
sin
,
,
2 800
0 5
3200
3 2
202. Efektivna vrijednost jakosti izmjeni
č
ne struje u krugu u kojem je spojen otpornik
(R=50
Ω
) je 5 A. Koliki je maksimalni napon na otporniku?
A) 14,2 V
B) 176 V
C) 250 V
D) 353 V
E) 370 V
rješenje:
(D)
I
ef
=5 A
R=50
Ω
U
0
=?
U
I
R
A
V
U
U
V
V
ef
ef
ef
=
⋅ =
⋅
=
=
⋅
=
⋅
=
5
50
250
2
250
1 41
352 5
0
Ω
,
,
203. Kugla volumena 60 dm
3
pliva na vodi tako da je 2/3 njenog volumena iznad vode.
Kolika je masa utega koji
ć
e držati cijelu kuglu pod vodom? Gusto
ć
a vode je 1000 kgm
-3
.
A) 40 g
B) 12 kg
C) 200 g
D) 40 kg
E) 30 kg
rješenje:
(D)
V=60 dm
3
V
neur
=2/3·60=40 dm
3
G=U
ρ
t
=1000 kgm
-3
m·g=V
neur.
·
ρ
t
·g
m=?
m=V
ne ur.
·
ρ
t
=40·10
-3
m
3
·1000 kgm
-3
=40 kg
204. Hidrostatski tlak vode, izmjeren na dnu jezera iznosi 150 kPa. Gusto
ć
a vode je 1000
kgm
-3
. Ako se za akceleraciju sile teže g uzme 10 ms
-2
, približna dubina jezera bit
ć
e:
A) 1,5 m
B) 15 m
C) 6,7 m
D) 2,5 m
E) 67 m
rješenje:
(B)
P=150 kPa
ρ
=1000 kgm
-3
h=?
P
g h
h
P
g
Pa
kgm
ms
m
= ⋅ ⋅
=
⋅
=
⋅
⋅
=
−
−
ρ
ρ
150 10
1000
10
15
3
3
2
161
205. Perioda izražena u sekundama kuglice koja se njiše na niti duga
č
koj 10 m je:
A)
π
B) 2
π
C) 1
D) 10
E) 10
rješenje:
(B)
l=10 m
T=?
T
l
g
m
ms
=
=
=
−
2
2
10
10
2
2
π
π
π
s
206. U strujnom krugu nalaze se tri otpornika. Dva od njih, jednaka s otporom 100 oma
svaki, spojena su paralelno, a tre
ć
i od 50 oma vezan je s njima u seriju. Nadomjesni otpor
tih otpornika (u omima) je:
A) 250
B) 150
C) 50
D) 66,7
E) 100
rješenje:
(E)
R
1
=R
2
=100
Ω
R
3
=50
Ω
R
u
=?
1
1
1
1
1
100
1
100
1
2
100
50
1
2
R
R
R
R
R
R
=
+
=
+
=
=
Ω
Ω
Ω
Ω
R
R
R
R
R
u
u
u
= +
=
+
=
3
50
50
100
Ω
Ω
Ω
207. Dva bakrena vodi
č
a imaju jednaku duljinu, a polumjeri njihovih popre
č
nih presjeka
odnose se na na
č
in: r
1
/r
2
=1/5. Omjer njihova otpora R
1
/R
2
je:
A) 0,2
B) 5
C) 25
D) 0,04
E) 0,4
rješenje:
(C)
l
1
=l
2
r
1
/r
2
=1/5
R
1
/R
2
=?
R
R
l
S
l
S
S
S
r
r
r
r
1
2
1
2
2
1
2
2
1
2
2
1
2
2
5
1
25
=
⋅
⋅
=
=
=
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝⎜
⎞
⎠⎟
=
ρ
ρ
π
π

163
212. Za koliko je stupnjeva temperatura vode na vrhu slapa niža od temperature pri dnu,
ako voda pada s visine 1 km? (c
vode
=4200 J/kgK, g=10 m/s
2
)
A) 4,2·10
7
B) 0,42
C) 0,0024
D) 2,4
E) 24
rješenje:
(D)
h=1 km=1000 m
Δ
t=?
Q
Ep
mc t
mgh
t
gh
c
ms
m
Jkg
K
K
=
=
=
=
⋅
=
−
−
−
Δ
Δ
10
1000
4200
2 38
2
1
1
,
213. Zraka svjetlosti izlazi iz vode u zrak. Ako pri tom prijelazu sinus kuta upadanja iznosi
0,5 a sinus kuta loma 0,65 indeks loma vode je:
A) 0,77
B) 1,3
C) 0,325
D) 0,65
E) 1,15
rješenje:
(B)
sin
α
=0,5
sin
β
=0,65
n=?
n
n
n
1
2
2
1
1
0 65
0 5
1 3
=
=
=
=
sin
sin
,
,
,
β
α
214. Kolika mora biti brzina satelita da bi se mogao gibati po kružnoj stazi oko Zemlje na
visini 3000 m? (u m/s) (g=10 m/s
2
, R
Zemlje
=6400 km)
A) 8·10
3
B) 64·10
3
C) 6,4·10
7
D) 253
E) 800
rješenje:
(A)
h=3000 m
R
z
=6400 km
v=?
mv
R
h
G M
m
R
h
v
G M
R
h
m kg
s
kg
m
v
m s
m s
z
z
z
z
z
2
2
11
3
1
2
24
3
5
3
6 67 10
6 10
6403 10
0 07905 10
7 905 10
+
=
⋅
⋅
+
=
⋅
+
=
⋅
⋅ ⋅
⋅
=
⋅
=
⋅
−
− −
(
)
,
,
/
,
/
164
215. Gubitak mase pri stvaranju jezgre litija iznosi 5,7·10
-29
g. Energija vezanja jezgre litija
prema tome iznosi (u džulima):
A) 5,1·10
-18
B) 5,1·10
-16
C) 5,1·10
-15
D) 5,1·10
-3
E) 5,1·10
-12
rješenje:
(C)
m=5,7·10
-29
g
E=?
E=mc
2
=5,7·10
-29
·10
-3
kg·(3·10
8
ms
-1
)
2
=5,13·10
-15
J
216. Skratimo li njihalo na 1/4 njegove duljine perioda
ć
e se
A) pove
ć
ati
č
etiri puta
B) smanjiti
č
etiri puta
C) pove
ć
ati šesnaest puta
D) pove
ć
ati dva puta
E) smanjiti dva puta
rješenje:
(E)
l
2
=1/4 l
T
2
=?
T
T
l
g
l
g
l
l
l
l
l
l
T
T
2
1
2
2
1
4
1
2
2
1
2
2
1
2
2
=
=
=
=
=
=
π
π
217. Elektri
č
no kuhalo priklju
č
eno na napon 200 V može za 7 minuta zagrijati 1 litru vode
od 20°C do vrenja. Koliki otpor ima grija
č
kuhala? (c
vode
=4200 J/kgK)
A) 0,8 oma
B) 3,3 oma
C) 1 om
D) 50 oma
E) 200 oma
rješenje:
(D)
U=200 V
t=7 min=7·60 s
m=1 kg
t
1
=20 °C
t
2
=100 °C
R=?
W
Q
U I t
m c
t
ako je I
U
R
U
t
R
m c
t
R
U
t
m c
t
V
s
kg
Jkg
K
K
=
⋅ ⋅ = ⋅ ⋅
=
⇒
⋅ = ⋅ ⋅
=
⋅
⋅ ⋅
=
⋅ ⋅
⋅
⋅
=
−
−
Δ
Δ
Δ
Ω
,
2
2
2
2
1
1
200
7 60
1
4200
80
50
218. Na krajevima kondenzatora u elektri
č
nom titrajnom krugu mijenja se napon pre-ma
jednadžbi U=(50 V) sin(10
4
·
π
s
-1
)t. Kapacitet kondenzatora iznosi 0,1 mikrofarad. Odredite
induktivitet zavojnice.

166
221. Na tijelo mase m, specifi
č
ne topline c i temperature t
1
prešla je koli
č
ina topline Q.
Kona
č
na temperatura tijela se može izra
č
unati iz izraza:
A) Q+t
1
B) Q/mc
C) Q-t
1
D) Q/mc+t
1
E) mc/Q
rješenje:
(D)
t
t
t
Q
mc t
t
Q
mc
t
t
Q
mc
= +
=
=
⇒
= +
1
1
Δ
Δ
Δ
222. U strujnom krugu nalazi se osigura
č
od 10 A. Koliko iznosi maksimalno dozvoljena
snaga struje (izražena u vatima) na otporniku od 20 oma?
A) 100
B) 200
C) 1000
D) 2000
E) 20
rješenje:
(D)
I=10 A
R=20
Ω
P=?
P
U I
U
I R
P
I
R
A
W
= ⋅
= ⋅
⇒
=
⋅ =
⋅
=
2
2
2
10
20
2000
Ω
223. Koliko fotona žutog svjetla valne duljine od 6·10
-7
m u jednoj sekundi odgovara snazi
od 1,65·10
-18
W (Planckova konstanta je 6,6·10
-34
Js)?
A) 1
B) 5
C) 100
D) 500
E) 1000
rješenje:
(B)
λ
=6·10
-7
m
t=1 s
P=1,65·10
-18
W
n=?
P
n h c
t
n h c
t
n
P
t
h c
W
m s
Js
ms
=
⋅ ⋅
= ⋅ ⋅
⋅
= ⋅ ⋅
⋅
=
⋅
⋅ ⋅
⋅
⋅
⋅ ⋅
=
−
−
−
−
λ
λ
λ
1 65 10
6 10
1
6 6 10
3 10
5
18
7
34
8
1
,
,
224. Brzina vode u rijeci je 3 km/sat. Motorni
č
amac ide uzvodno brzinom od 10 km/sat.
Kojom brzinim bi
č
amac išao niz rijeku?
A) 7
B) 10
167
C) 13
D) 16
E) 30
rješenje:
(D)
v
1
=3 km/sat
v
2
=10 km/sat
v=?
v=v
2
+2v
1
=10km/h+2·3km/h=16 km/h
225. Kota
č
vozila koje se kre
ć
e brzinom 60 km/h ima radijus 65 cm. Koliko približno okre-
ta u sekundi izvrši kota
č
?
A) 5
B) 3
C) 4
D) 7
E) 2
rješenje:
(C)
v=60 km/h=16,66 ms
-1
r=65 cm=0,65 m
n=? s
-1
n
r
v
n
v
r
ms
m
s
⋅
=
=
=
⋅
⋅
=
−
−
2
2
16 66
2 0 65
3 14
4 08
1
1
π
π
,
,
,
,
226. Koliko se smanjila unutrašnja energija olovne kugle mase 600 g koja je bila zagrijana
na 350°C pa ohla
đ
ena na 25°C? (c
olova
=120 Jkg
-1
K
-1
)
A) 234 kJ
B) 2,34 MJ
C) 23,4 kJ
D) 2340 J
E) 234 J
rješenje:
(C)
m=600 g=0,6 kg
t
1
=350 °C
t
2
=25 °C
Δ
U=?
Δ
U=
Δ
Q=mc
Δ
t=0,6kg·120Jkg
-1
K
-1
·325K=23400J=23,4 kJ
227. Period prvog njihala je 8 s, a drugog 6 s. Kako se odnose njihove duljine L
1
:L
2
?
A) 8
1/2
:6
1/2
B) 6:8
C) 9:16
D) 8:6
E) 16:9
rješenje:
(E)
T
1
=8 s
T
2
=6 s
L
1
:L
2
=?
T
T
L
g
L
g
T
T
L
L
1
2
1
2
1
2
2
2
1
2
2
2
=
⇒
=
π
π

169
E) E=m/c
2
rješenje:
(A)
232. Pretpostavimo da se kod fisije urana 0,1% mase prisutnog urana transformira u energi-
ju. Koliko je približno energije u džulima proizvedeno fisijom 1 kg urana?
A) 17·10
7
B) 37·10
20
C) 23·10
28
D) 9·10
13
E) 9·10
20
rješenje:
(D)
m=0,1%·1 kg
E=?
E=mc
2
=0,001kg·3
2
·10
16
m
2
s
-2
=9·10
13
J
233. Grani
č
na energija fotona koja uzrokuje fotoelektri
č
ni efekt u metalu je 4,95·10
-19
J.
Tome približno odgovara energija u eV (naboj elektrona je 1,6·10
-19
C)?
A) 1
B) 3
C) 5
D) 8
E) 1,2·10
-19
rješenje:
(B)
E=4,95·10
-19
J
E=? eV
E
J
C
eV
=
⋅
⋅
=
−
−
4 95 10
1 6 10
3 09
19
19
,
,
,
234. Svjetlo valne duljine 500 nm pada na opti
č
ku mrežicu i ogiba se pod kutom prvog
ogibnog maksimuma kojeg je sinus jednak 0,8. Koliko iznosi konstanta opti
č
ke mrežice u
μ
m?
A) 40
B) 4
C) 0,4
D) 0,625
E) 0,5
rješenje:
(D)
λ
=500 nm
k=1
sin
α
=0,8
d=?
k
d
d
k
m
m
m
⋅ = ⋅
= ⋅ = ⋅
⋅
=
⋅
=
−
−
λ
α
λ
α
μ
sin
sin
,
,
1 500 10
0 8
625 10
0 625
9
9
235. Jedna godina svjetlosti je udaljenost koju svjetlost prije
đ
e za godinu (365) dana brzi-
nom od 3·10
5
km/s. Kolika je ta udaljenost?
A) 9,5·10
9
km
B) 95·10
13
km
C) 9,5·10
12
km
170
D) 950·10
11
km
E) 95·10
10
km
rješenje:
(C)
t=365 dana
v=3·10
5
km/s
s=?
s=v·t=3·10
5
km/s·365·86400 s=9,46·10
12
km
236. Vlak koji se kre
ć
e brzinom od 20 kmh
-1
po
č
inje ubrzavati i nakon 50 s postiže brzinu
60 kmh
-1
. Kolka je akceleracija u tom vremenskom intervalu?
A) 0,8 m/s
2
B) 0,2 ms
-2
C) 1,4 ms
-2
D) 0,6 ms
-2
E) 1,2 ms
-2
rješenje:
(B)
v
1
=20 kmh
-1
=5,555 ms
-1
Δ
t=50 s
v
2
=60 kmh
-1
=16,666 ms
-1
a=?
a
v
v
t
s
ms
s
ms
=
−
=
−
=
−
−
−
2
1
1
1
2
16 666
5 555
50
0 22
Δ
,
,
,
237. Ako ispustimo kamen s vrha tornja visokog 50 m, s kojom
ć
e brzinom udariti o
zemlju?
A) 96 km/h
B) 120 km/h
C) 113 km/h
D) 107 km/h
E) 130 km/h
rješenje:
(C)
h=50 m
v=?
v
gh
ms
m
ms
km h
=
=
⋅
⋅
=
=
−
−
2
2 9 81
50
31 32
112 755
2
1
,
,
,
/
238. Automobil mase 800 kg kre
ć
e se brzinom od 40 km/h. Kolika mora biti sila ko
č
e-nja
da se zaustavi nakon 30 m?
A) 330 N
B) 3300 N
C) 165 N
D) 16500 N
E) 1650 N
rješenje:
(E)
m=800 kg
v=40 km/h=11,11 m/s
s=30 m
F=?
v
as
a
v
s
F
m a
m
v
s
kg
m s
m
N
=
⇒
=
= ⋅ = ⋅
=
⋅
⋅
=
−
2
2
2
800
11 11
2 30
1645 76
2
2
2
2
2
,
,

172
E) 10 m/s
rješenje:
(A)
λ
=15 m
T=3 s
v=?
v
T
m
s
ms
=
=
=
−
λ
15
3
5
1
243. Kroz površinu od 0,5 m
2
prolazi elektromagnetski val snage 0,1 W. Intenzitet toga vala
(W/m
2
) je:
A) 0,1
B) 0,2
C) 1
D) 2
E) 0,05
rješenje:
(B)
s=0,5 m
2
P=0,1 W
I=?
I
P
S
w
m
W m
= =
=
0 1
0 5
0 2
2
2
,
,
,
/
244. Rad plina pri volumnoj ekspanziji od 40 litara, uz stalni tlak, iznosi 20 J. Pri tome je
veli
č
ina stalnog tlaka u Pa jednaka:
A) 800
B) 600
C) 500
D) 200
E) 100
rješenje:
(C)
Δ
V=40 l=40·10
-3
m
3
W=20 J
p=?
W
p
V
P
W
V
J
m
Pa
Pa
= ⋅
=
=
⋅
=
⋅
=
−
Δ
Δ
20
40 10
0 5 10
500
3
3
3
,
245. Koliki je volumen jednog mola idealnog plina (u m
3
) kome je temperatura 500 K a
tlak 415 Pa (plinska konstanta je 8,3 Jmol
-1
K
-1
)?
A) 1
B) 10
C) 100
D) 1000
E) 10000
rješenje:
(B)
n=1 mol
T=500 K
P=415 Pa
V=?
PV
nRT
V
nRT
P
mol
Jmol K
K
Pa
m
=
=
=
⋅
⋅
=
−
−
1
8 3
500
415
10
1
1
3
,
246. Omjer kineti
č
kih energija dvaju tijela jednakih masa je 5:20. Omjer brzina tih tijela je:
A) 1/4
173
B) 0,5
C) 5/20
D) 0,25
E) 4/1
rješenje:
(B)
m
1
=m
2
E
k1
:E
k2
=5:20
v
1
:v
2
=?
E
E
m v
m v
v
v
v
v
E
E
k
k
k
k
1
2
1
2
2
2
1
2
2
2
1
2
1
2
2
2
5
20
1
2
0 5
=
=
=
=
= =
,
247. Tri otpornika od 2, 3 i 0,4 oma spojena su paralelno. Ukupni otpor kombinacije je (u
omima)?
A) 3
B) 0,3
C) 0,03
D) 3·10
-3
E) 3·10
-4
rješenje:
(B)
R
1
=2
Ω
R
2
=3
Ω
R
3
=0,4
Ω
=2/5
Ω
R
u
=?
1
1
1
1
1
2
1
3
1
1
2
1
3
5
2
3 2 15
6
20
6
6
20
3
10
0 3
1
2
3
2
5
R
R
R
R
R
u
u
=
+
+
=
+
+
=
+
+
= + +
=
=
=
=
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
,
248.
Č
amac ide niz rijeku brzinom od 14 km/h. Brzina vode u rijeci je 4 km/sat. Kojom bi
brzinom
č
amac išao uzvodno?
A) 4 km/sat
B) 6 km/sat
C) 10 km/sat
D) 14 km/sat
E) 18 km/sat
rješenje:
(B)
v
č
(nizv)
=14 km/h
v
r
=4 km/h
v
č
(
uzv)
=?
v
č
=v
č
(nizv)
-v
r
=14 km/h-4 kmh=10 km/h
v
č
(uzv)
=v
č
-v
r
=10 km/h-4 km/h=6 km/h

175
E) slobodno pada
rješenje:
(B)
253. Pri horizontalnom hicu na tijelo djeluje:
A) konstantna sila u horizontalnom smjeru
B) samo otpor zraka
C) sila u smjeru tangente na putanju
D) konstantna sila u smjeru vertikalnom prema dolje
E) rezultantna sila u smjeru putanje
rješenje:
(D)
254. Za svaki metar dubine u vodi (gusto
ć
a vode je 1000 kg/m
3
) se hidrostatski tlak promi-
jeni za:
A) 9,81 kPa
B) 9,81 Pa
C) 9,81 mPa
D) 9,81 MPa
E) 981 Pa
rješenje:
(A)
h=1 m
ρ
=1000 kg/m
3
P=?
P=
ρ
·g·h=1000 kgm
-3
·9,81 ms
-2
·1m=9810 Pa=9,81 kPa
255. Napon na polovima izvora s unutrašnjim otporom od 0,25 oma pri struji optere
ć
enja
od 4 ampera iznosi 23 volta. Elektromotorna sila toga izvora je:
A) 23 V
B) 24 V
C) 22 V
D) 16 V
E) 39 V
rješenje:
(B)
R
u
=0,25
Ω
I=4 A
U=23 V
EMS=?
R
U
I
V
A
EMS
I R
R
A
V
v
u
v
=
=
=
=
+
=
+
=
23
4
5 75
4
0 25
5 75
24
,
(
)
( ,
,
)
Ω
Ω
Ω
256. Koliki je otpor voltmetra (u omima) za mjerno podru
č
je od 250 V ako struja u njemu
ne smije prije
ć
i vrijednost od 20 mA?
A) 1250
B) 5000
C) 12,5
D) 5
E) 12500
rješenje:
(E)
176
U=250 V
I=20 mA
R=?
I
U
R
R
U
I
V
A
=
=
=
⋅
=
−
250
20 10
12500
3
Ω
257. Titrajni krug sastavljen od zavojnice i plo
č
astog kondenzatora s zrakom me
đ
u plo
č
a-
ma ima frekvenciju f. Ako se me
đ
u plo
č
e unese dielektrik relativne permitivnosti 81, tada
ć
e frekvencija f
1
iznositi:
A) f
1
=f
B) f
1
=81 F
C) f
1
=f/81
D) f
1
=f/9
E) f
1
=9f
rješenje:
(D)
ε
r
=81
f
1
=?
C
S
d
C
C
r
=
⋅ ⋅
=
ε ε
0
1
81
f
LC
f
f
L
C
LC
f
f
=
=
⋅
=
⇒
=
1
2
1
2
81
1
2
1
9
1
9
1
1
π
π
π
258. Na elasti
č
noj opruzi konstante elasti
č
nosti k obješeno je tijelo mase m. Frekvencija
ovakvog harmonijskog oscilatora je:
A) upravno razmjerna s m
B) upravno razmjerna s m
2
C) obrnuto razmjerna s m
D) upravno razmjerna s m/k
E) obrnuto razmjerna s m
1/2
rješenje:
(E)
f
m
k
f
m
=
⇒
≈
1
2
1
1
2
π
259. Broj titraja u jednoj minuti je 150. Frekvencija takvog titranja je:
A) 150 Hz
B) 0,4 Hz
C) 0,007 Hz
D) 2,5 Hz
E) 25 Hz
rješenje:
(D)
f=150 min
-1
f=? Hz
f
s
Hz
=
=
150
60
2 5
,

178
E) L/2
rješenje:
(E)
263. Koju
ć
e valnu duljinu (u nm) imati svjetlost što je emitira atom kad prelazi iz drugog
pobu
đ
enog stanja E
3
u prvo pobu
đ
eno stanje E
2
, ako se zna da je E
3
-E
2
=3·10
-19
J i
h=6,6·10
-34
Js?
A) 330
B) 400
C) 660
D) 1200
E) 6600
rješenje:
(C)
E
3
-E
2
=3·10
-19
J
λ
=?
E
E
h c
h c
E
E
Js
ms
J
m
nm
3
2
3
2
34
8
1
19
7
6 6 10
3 10
3 10
6 6 10
660
−
= ⋅
=
⋅
−
=
⋅
⋅ ⋅
⋅
=
⋅
=
−
−
−
−
λ
λ
,
,
264. Svjetlost upada na dijamantnu plo
č
icu pod kutem u koji je upravo kut polarizacije ili
Brewsterov kut za dijamant. Ako je sinus toga kuta 0,92, a njegov kosinus 0,38, indeks
loma dijamanta je:
A) 0,35
B) 0,54
C) 1,30
D) 0,41
E) 2,42
rješenje:
(E)
sin
α
=0,92
cos
α
=0,38
n=?
tg
n
n
α
α
α
=
=
=
=
sin
cos
,
,
,
0 92
0 38
2 42
265. Iz de Broglieve relacije zaklju
č
ujemo da je valna duljina brzih nabijenih
č
estica (elek-
trona, protona, iona):
A) upravno proporcionalna naboju
č
estica
B) upravno proporcionalna brzini
č
estica
C) upravno proporcionalna masi
č
estica
D) upravno proporcionalna koli
č
ini gibanja
č
estica
E) obrnuto proporcionalna koli
č
ini gibanja
č
estica
rješenje:
(E)
λ
λ
=
⋅
≈
⋅
h
m v
m v
1
266. Jeka se
č
uje jednu sekundu pošto je proizveden ton. Ako je brzina zvuka 340 m/s,
koliko je daleko površina refleksije?
179
A) 340 m
B) 50 m
C) 680 m
D) 170 m
E) 1050 m
rješenje:
(D)
t=1 s
v=340 m/s
d=?
Udaljenost površine refleksije jednaka je polovici prije-
đ
enog puta:
d
s
v t
s
m
m
s
= = ⋅ =
⋅
=
2
2
340
1
2
170
267. Duljina sekundnog njihala (tj. onog kojem je poluperiod 1 s) iznosi na ekvatoru
(g=9,72 ms
-2
)
A) 2,99 m
B) 3,99 m
C) 1,99 m
D) 0,99 m
E) 5 m
rješenje:
(D)
T=2 s
l=?
T
l
g
l
T
g
s
ms
m
m
=
=
⋅ =
⋅
⋅
=
=
−
2
4
4
9 72
4 3 14
0 9858
0 99
2
2
2
2
2
π
π
,
,
,
,
268. Tijelo mase 10 kg giba se brzinom 2 m/s. Drugo tijelo mase 15 kg giba se u istom
smjeru kao i prvo brzinom 3 m/s. Poslije sudara tijela se gibaju slijepljena zajedno. Odredi-
te brzinu tijela poslije sudara.
A) 2,2 m/s
B) 2,6 m/s
C) 2,8 m/s
D) 3,0 m/s
E) 2,0 m/s
rješenje:
(B)
m
1
=10 kg
v
1
=2 m/s
m
2
=15 kg
v
2
=3 m/s
v=?
m v
m v
m
m
v
v
m v
m v
m
m
kg
ms
kg
ms
kg
kg
ms
1 1
2
2
1
2
1 1
2
2
1
2
1
1
1
10
2
15
3
10
15
2 6
+
=
+
⋅
=
+
+
=
⋅
+
⋅
+
=
−
−
−
(
)
,
269. Elektri
č
ni titrajni krug sastoji se od zavojnice i kondenzatora. Kako se promijeni
period tog titrajnog kruga ako se kapacitet kondenzatora pove
ć
a
č
etiri puta, a indukti-vitet
zavojnice ostane isti?
A) smanji se dva puta

181
A) na polovini
B) 0,5 m od drugog
C) 0,5 m od prvog
D) 0,75 m od prvog
E) 0,25 m od prvog
rješenje:
(C)
l=2 m
Momenti sila F
1
i F
2
s obzirom na to
č
ku A moraju biti jednaki.
F
1
=3F
2
r
1
=?
M
1
=M
2
r
1
+r
2
=l
F
1
r
1
=F
2
r
2
jer je F
1
=3F
2
bit
ć
e
r
1
+3r
1
=2 m
3F
2
r
1
=F
2
r
2
4r
1
=2 m
3r
1
=r
2
r
1
=0,5 m
273. Voltmetar ima otpor 120
Ω
. Koliki
ć
e napon pokazivati ako je priklju
č
en na bateriju
č
ija je elektromotorna sila jednaka 9 V i
č
iji je unutarnji otpor jednak 15
Ω
?
A) 8 V
B) 9 V
C) 1 V
D) 0,1 V
E) 6 V
rješenje: (A)
R=120
Ω
EMS=9 V
R
u
=15
Ω
U=?
I
EMS
R
R
U
I R
EMS R
R
R
V
V
u
u
=
+
= ⋅ =
⋅
+
=
⋅
+
=
9
120
120
15
8
Ω
Ω
Ω
274. U dijagramu ovisnosti brzine o vremenu v=f(t) za gibanje nekog tijela površinom
ispod krivulje brzine predo
č
eno je:
A) srednje ubrzanje tijela u vremenu t
B) srednja brzina tijela
C) put pre
đ
en u vremenu t
D) rad tijela izvršen u vremenu t
E) kineti
č
ka energija tijela
rješenje:
(C)
275. U homogenom magnetskom polju indukcije 1,5 T jednoliko se giba vodi
č
duljine 10
cm. Njime te
č
e struja 2 A, brzina mu je 1 m/s a vodi
č
je okomit na polje. Snaga potrebna za
ovo gibanje jest:
A) 3 W
B) 40 W
C) 0,3 W
D) 1,5 W
E) 33 W
182
rješenje:
(C)
B=1,5 T
l=10 cm=0,1 m
I=2 A
v=1 ms
-1
α
=90°
P=?
P
W
t
jer je
W
F s
P
F s
t
jer je
F
B I l
P
B I l
s
t
jer je
s
t
v
P
B I l v
T
A
m
ms
W
=
= ⋅
⇒
= ⋅
= ⋅ ⋅ ⋅
⇒
= ⋅ ⋅ ⋅
=
⇒
= ⋅ ⋅ ⋅ =
⋅
⋅
⋅
=
−
sin
,
,
,
α
1 5
2
0 1
1
0 3
1
276. Koliko je topline potrebno da bi se 3 kg leda temperature-20 °C rastopilo i da bi se
temperatura tako dobivene vode povisila na 80 °C. (Specifi
č
ni toplinski kapacitet leda je
2100 Jkg
-1
k
-1
, specifi
č
ni toplinski kapacitet vode je 4200 Jkg
-1
k
-1
a specifi
č
na toplina talje-
nja leda je 3,3·10
5
J/kg
A) 1,5·10
6
K/kg
B) 2,1·10
6
J
C) 3,4·10
6
J
D) 4,7·10
6
J
E) 5,6·10
6
J
rješenje:
(B)
m=3 kg
t
1
=-20 °C
t
2
=80 °C
Q=?
Q=Q
1
+Q
2
+Q
3
Q
1
=m·c
l
·
Δ
T
l
toplina potrebna za zagrijavanje leda od -20 °C do 0 °C
Q
2
=m·
λ
l
toplina potrebna za taljnenje leda
Q
3
=m·c
v
·
Δ
t
v
toplina potrebna za zagrijavanje vode
Q= m·c
l
·
Δ
T
l
+ m·
λ
l
+ m·c
v
·
Δ
t
v
Q=3kg·2100Jkg
-1
K
-1
·20K+3kg·3,3·10
5
Jkg
-1
K
-1
+3kg·4200Jkg
-1
K
-1
·80K
Q=126000J+990000J+1008000J
Q=2124000 J
Q=2,124·10
6
J
277.
Č
amac je usmjeren preko rijeke pod kutom 90
°
u odnosu na smjer njezina toka. Brzi-
na
č
amca prema vodi je 5 m/s, a brzina toka rijeke je 2 m/s. Najkra
ć
a udaljenost me
đ
u
obalama jest 200 m. Od jedne do druge obale
č
amac plovi:
A) 4 s
B) 4 min
C) 40 s
D) 60 s
E) 6 min
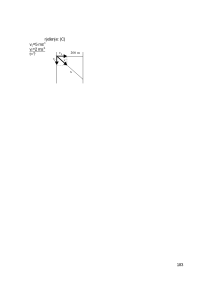
184
D) 28 m
E) 32 m
rješenje:
(B)
t
1
=2 s
v=4 m/s
t
2
=4 s
v
1
=4 m/s
v
2
=4 m/s
t
3
=3 s
s=?
s
s
s
s
s
a
t
v
t
a
t
s
v t
v
t
v
t
s
ms
s
ms
s
ms
s
s
m
m
m
s
m
i
=
+
+
=
⋅
+
⋅ +
⋅
=
⋅
+
⋅ +
⋅
=
⋅ +
⋅ +
⋅
=
+
+
=
−
−
−
1
2
3
1
1
2
2
2
2
3
2
1
2
3
1
1
1
2
2
2
2
4
2
2
4
4
4
3
2
4
16
6
26
s
1
-jednoliko ubrzano gibanje
s
2
- jednoliko gibanje
s
3
- jednoliko usporeno gibnje
281. Elektri
č
na pe
ć
priklju
č
ena je na gradsku mrežu napona 220 V. Pe
ć
ima 3 m dugu
grija
č
u nit i za 20 min povisi u prostoriji temperaturu za 20 °C. Koliko mora biti duga
č
ka ta
nit ako isto povišenje temperature u prostoriji želimo posti
ć
i za 15 min?
A) 2,25 m
B) 2 m
C) 5 m
D) 1,5 m
E) 3,5 m
rješenje:
(A)
U=220 V
l
1
=3 m
t
1
=20 min
Δ
t
1
=20 K
t
2
=15 min
Δ
t
2
=
Δ
t
1
l
2
=?
Q = W
Q = Q
1
2
U t
R
U t
R
U t
l
S
U t
l
S
t
l
t
l
l
t
l
t
l
m
l
m
2
1
1
2
2
2
2
1
1
2
2
2
1
1
2
2
2
2
1
1
2
2
15
3
20
2 25
=
⋅
=
⋅
=
=
⋅
=
⋅
=
ρ
ρ
min
min
,
Potrebna toplina jednaka je izvršenom
radu el. struje, a ta toplina je u oba slu
č
aja
ista.
Uvrstimo li za R
l
S
=
⋅
ρ
dobijamo
Presjeci (S) i otpornosti (
ρ
) su isti.
282. Nogometnu loptu volumena 2,8 litara (u napuhanom stanju) pumpamo ru
č
nom
pumpom, koja u jednom hodu ru
č
ice daje 200 cm
3
zraka. Lopta je u po
č
etku pumpanja
185
potpuno ispražnjena, a pumpamo je do tlaka od 180 kPa. Koliko puta treba potisnuti ru
č
icu
pumpe?
A) 20
B) 22
C) 30
D) 38
E) 25
rješenje:
(E)
V
1
=2,8 l
V
2
=200 cm
3
=0,2 l
p
1
=180 kPa
p
2
=1,013·10
5
Pa
n=?
p V
p nV
n
p V
p V
Pa
l
o
Pa
l
1
1
2
2
1
1
2
2
3
5
180 10
2 8
1 13 10
0 2
24 876
25
=
=
=
⋅
⋅
⋅
⋅
=
=
,
,
,
,
283. Udaljenost izme
đ
u dviju stanica metroa iznosi 2 km, koju kompozicija metroa prije
đ
e
za 140 s. Maksimalna brzina koju metro postigne na tom putu iznosi 60 km/h. Na po
č
etku i
na kraju svog gibanja metro se kre
ć
e stalnim ubrzanjem jednakim po apsolutnoj veli
č
ini.
Koliko iznosi to ubrzanje?
A) 2,5 ms
-2
B) 0,83 ms
-2
C) 10 ms
-2
D) 0,41 ms
-2
E) 7,34 ms
-2
rješenje:
(B)
s=2 km
t=140 s
v=60 km/h
a
1
=a
2
=a
a=?
s
a t
v
t
a t
t
t
t
t
i
t
t
t
t
t
s
v t
t
v t
v t
t
v t
t
v t
v t
v t
t
t
s
v
t
t
s
t
t
m
s
t
t
s
t
t
s
t
s
t
s
a
v
t
ms
s
=
⋅
+
⋅ +
⋅
+ +
=
=
⇒
+
=
=
⋅
+ ⋅ +
⋅
=
⋅
+ ⋅
= ⋅ + ⋅
+
=
+
=
⋅ −
+
=
−
−
= −
+
=
− = −
=
=
=
=
−
1
2
2
2
3
2
1
2
3
1
3
1
2
1
2
1
2
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
1
2
2
2
2
2
2
2
2
2
140
1
2000
16 67
2
140
119 97
20
20
16 67
20
0 833
(
)
,
,
,
,
ms
−
2

187
C) 12,8·10
4
cm/s
D) 1,2·10
8
m/s
E) 128 m/s
rješenje:
(B)
B=18,2·10
-4
T
R=4 cm=4·10
-2
m
v=
mv
R
Q v B
v
Q R B
m
C
T
m
kg
m s
2
19
4
2
31
6
1 6 10
18 2 10
4 10
9 1 10
12 8 10
= ⋅ ⋅
= ⋅ ⋅ =
⋅
⋅
⋅
⋅ ⋅
⋅
=
⋅
−
−
−
−
,
,
,
,
/
287. Na užetu duljine 1 m obješen je uteg mase 1 kg. Uže može izdržati najve
ć
u silu 11 N.
Koliko visoko možemo podi
ć
i uteg iz ravnotežnog položaja da se pri njihanju uže ne preki-
ne (g=10 m/s
2
)
A) 0,02 m
B) 20 cm
C) 5 cm
D) 50 cm
E) 0,5 cm
rješenje:
(C)
l=1 m
m=1 kg
F
N
=11 N
h=?
Sila napetosti mora biti ve
ć
a ili jednaka zbroju težine i centrifugalne
sile.
F
G
F
mg
mv
l
gh
F
mg
m
gh
l
mg
mgh
l
h
F
mg l
mg
N
kg
ms
m
kg
ms
m
cm
N
c
N
N
= +
=
+
=
=
+
=
+
=
−
⋅
=
−
⋅
⋅
⋅
⋅
=
=
−
−
2
2
2
2
2
2
2
2
11
1
10
1
2 1
10
0 05
5
v
(
)
(
)
(
)
,
288. Kroz metalnu žicu pro
đ
e u 10 sekundi 10
21
elektrona. Pri tome se u žici razvije toplina
od 10
3
J. Otpor žice je: (naboj elektrona e=1,6·10
-19
C)
A) 20
Ω
B) 390
Ω
C) 0,195
Ω
D) 19,5
Ω
E) 0,39
Ω
rješenje:
(E)
t=10 s
n=10
21
e
Q=10
3
J
R=?
I
n Q
t
C
s
A
Q
R I
t
R
Q
I
t
J
A
s
e
=
⋅
=
⋅
⋅
=
= ⋅ ⋅
⇒
=
⋅
=
⋅
=
−
10
1 6 10
10
16
10
16
10
0 390
21
19
2
2
3
2
2
,
,
Ω
188
289. Odredite omjer naboja i mase (Q/m) za
č
esticu koja se ubrza iz mirovanja i posti-gne
brzinu 1,2·10
7
m/s kroz razliku potencijala od 400 V.
A) 2 C/kg
B) 1,44·10
14
C/kg
C) 2·10
12
C/kg
D) 1,8·10
11
C/kg
E) 1,6·10
-19
C
rješenje:
(D)
v=1,2·10
7
ms
-1
U=400 V
Q/m=?
mv
Q U
Q
m
v
U
ms
V
C kg
2
2
7
1 2
11
2
2
1 2 10
2 400
1 8 10
= ⋅
=
=
⋅
⋅
=
⋅
−
( ,
)
,
/
290. Na izvor napona
č
iji je unutrašnji otpor R
u
=1
Ω
, priklju
č
en je otpor R
1
=10
Ω
. Koliko
puta
ć
e se smanjiti jakost struje kroz otpor R
1
ako se paralelno s otporom R
1
u strujni krug
ukop
č
a R
2
=5
Ω
?
A) 1,18 puta
B) 2,3 puta
C) 3,31 puta
D) 2,13 puta
E) 5 puta
rješenje: (A)
R
u
=1
Ω
R
1
=10
Ω
R
2
=5
Ω
I/I
1
=?
I
E
R
R
E
E
u
=
+
=
+
=
1
1
10
11
Ω
Ω
Ω
I
E
R
R
E
R
R R
R
R
E
E
I
I
I
I R
I R
I
I R
R
I
I
I
R
R
E
E
I
I
E
E
u
u
=
+ ′
=
+
+
=
+
=
+
=
=
+
=
=
+
=
+
=
=
=
=
1
2
1
2
1
2
1
1
2
2
1
1
1
2
1
1
2
1
1
50
15
3
13
1
3
13
1 2
13
11
13
13
11
1 18
Ω
Ω
Ω
Ω
Ω
Ω
,

190
293. U televizijskoj se cijevi elektroni ubrzavaju razlikom potencijala od 20 kV. Kolika je
najmanja valna duljina rendgenskih zraka što ih emitira ekran (h=6,626·10
-34
Js, c=3·10
8
ms
-1
, e=1,6·10
-19
C)
A) 6,6·10
-34
m
B) 6,2·10
-11
m
C) 2·10
-8
m
D) 1,6·10
-8
m
E) 1,9·10
-9
m
rješenje:
(B)
U=20 kV
λ
=?
h c
Q U
h c
Q U
Js
ms
C
V
m
⋅ = ⋅
=
⋅
⋅
=
⋅
⋅ ⋅
⋅
⋅ ⋅
=
⋅
−
−
−
−
λ
λ
6 626 10
3 10
1 6 10
20 10
6 21 10
34
8
1
19
3
11
,
,
,
294. Motorkota
č
prije
đ
e tre
ć
inu puta brzinom 10 km/h, drugu tre
ć
inu puta brzinom 20
km/h i posljednju tre
ć
inu brzinom 60 km/h. Odredite srednju brzinu gibanja motorkota
č
a.
A) 20 km/h
B) 18 km/h
C) 7 m/s
D) 30 km/h
E) 36 m/s
rješenje:
(B)
v
1
=10 km/h
v
2
=20 km/h
v
3
=60 km/h
v
=?
v
s
t
s
s
v
s
v
s
v
v
v
v
v
kmh
kmh
kmh
kmh
kmh
= =
+
+
=
+
+
=
+
+
=
+ +
=
−
−
−
−
−
3
3
3
3
1
1
1
3
1
10
1
20
1
60
3
6 3 1
60
18
1
2
3
1
2
3
1
1
1
1
1
295. Njihalo ima nit dugu 1 m, a masu 1 kg. Kroz ravnotežni položaj masa njihala prolazi
brzinom 1 m/s. Napetost niti u tom trenutku iznosi:
A) 9,81 N
B) 10,81 N
C) 20,81 N
D) 0,81 N
E) 1,081 N
rješenje:
(B)
l=1 m=r
m=1 kg
v=1 ms
-1
N=?
N
mg
mv
r
kg
ms
kg ms
m
N
=
+
=
⋅
+
=
−
−
2
2
1 2
1
9 81
1
1
1
10 81
,
(
)
,
191
296. Koliki je omjer centripetalne akceleracije Mjeseca u kruženju oko Zemlje i akceleraci-
je sile teže na površini Zemlje ako je udaljenost Zemlja-Mjesec 384000 km, a vrijeme
ophoda Mjeseca oko Zemlje 27,3 dana?
A) 2,78·10
-4
B) 2,78·10
-2
C) 5,56·10
-4
D) 5,56·10
-2
E) 55,6·10
-1
rješenje:
(A)
R=384000 km
T=27,3 dana
a/g=?
a
T
r
s
m
ms
a
g
ms
ms
=
⎛
⎝⎜
⎞
⎠⎟
⋅ =
⋅
⋅
⋅
⋅
=
⋅
=
⋅
=
⋅
−
−
−
−
−
−
2
2 3 14
27 3 86400
384 10
2 72 10
2 72 10
9 81
2 78 10
2
2
2
6
3
2
3
2
2
4
π
(
, )
(
,
)
,
,
,
,
297. Cilindri
č
na posuda visine H=2 m ima kružni otvor polumjera r=0,02 m na visini h=0,5
m od dna posude. Kolika sila djeluje na
č
ep stavljen u kružni otvor ako je posu-da do vrha
napunjena vodom? (gusto
ć
a vode je 1000 kgm
-3
, g=9,81 ms
-2
)
A) 6,28 N
B) 12,57 N
C) 18,48 N
D) 25,13 N
E) 31,4 N
rješenje:
(C)
H=2 m
r=0,02 m
h=0,5 m
F=?
p
F
S
F
r
F
p r
H
h
g r
F
m
m
kgm
ms
m
N
= =
= ⋅
=
− ⋅ ⋅ ⋅
=
−
⋅
⋅
⋅
⋅
=
−
−
2
2
2
3
2
2
2
2
0 5
1000
9 81
0 02
3 14
18 48
π
π
ρ
π
(
)
(
,
)
,
,
,
,
298. Most
č
eli
č
ne konstrukcije duga
č
ak je 100 m pri 0°C. Koliki mora biti procjep koji
kompenzira promjenu dužine ako se o
č
ekuje godišnja promjena temperature od -20 °C do
+40 °C? (koeficijent linearnog širenja
č
elika
β
=10
-5
/K)
A) 2 cm
B) 3 cm
C) 4 cm
D) 5 cm
E) 6 cm
rješenje:
(E)
l
0
=100 m
t
0
=0°C
t
1
=-20°C
t
2
=+40°C
Δ
l=?
l
l
t
m
K
K
m
l
l
t
m
K
K
m
l
l
l
m
m
m
cm
40
0
5
1
20
0
5
1
40
20
1
100
1 10
40
100 04
1
100
1 10
20
99 98
100 04
99 98
0 06
6
=
+
=
+
⋅
=
=
+
=
−
⋅
=
=
−
=
−
=
=
−
−
−
−
−
−
(
)
(
)
,
(
)
(
)
,
,
,
,
βΔ
βΔ
Δ

193
C) 2 puta
D) tlak se ne mijena
E) 1,5 puta
rješenje:
(C)
t
1
=18°C=291 K
t
2
=309°C=528 K
P
2
=?
p
T
p
T
p
p
T
T
p
T
T
p
K
K
p
p
2
2
1
1
2
1
2
1
2
2
1
1
1
1
582
291
2
=
⇒
=
⇒
=
⋅
=
⋅
=
302. To
č
ka A nalazi se 30 m iznad to
č
ke B. Iz to
č
ke A ispustimo kamen. Iz to
č
ke B ispusti-
mo drugi kamen jednu sekundu nakon ispuštanja prvog kamena. S koje je visine ispušten
prvi kamen ako oba padnu na tlo u istom trenutku?
A) 35 m
B) 50 m
C) 55 m
D) 62 m
E) 78 m
rješenje:
(D)
h
g
t
h
g
t
uvrsti za
h
g
t
g
t
g
t
t
g
t
gt
gt
g
gt
g
t
s
h
g
t
ms
s
m
=
−
=
−
=
−
=
− +
−
=
− +
=
+
=
=
=
⋅
=
−
2
30
2
1
2
2
30
2
2
1
2
30
2
2
30
2
3 56
2
9 81
2
3 56
62 16
2
2
2
2
2
2
2
2
2
2
(
)
(
)
,
,
( ,
)
,
303. Uteg mase 0,5 kg visi na niti duljine 1 m. Uteg otklonimo iz položaja ravnoteže i
pustimo da titra. Kolika je napetost niti u
č
asu kad uteg prolazi položajem ravnoteže brzi-
nom 0,7 m/s?
A) 4,8 N
B) 6 N
C) 7,2 N
D) 5,2 N
E) 6,8 N
rješenje:
(D)
194
m=0,5 kg
l=1 m=R
v=0,7 ms
-1
N=?
N
F
F
mv
R
mg
kg
ms
m
kg
ms
N
N
N
c
g
=
+
=
+
=
⋅
+
⋅
=
=
−
−
2
1 2
2
0 5
0 7
1
0 5
9 81
5 15
5 2
,
( ,
)
,
,
,
,
304. Balon ukupne mase 200 kg spušta se konstantnom brzinom. Kolika je masa balasta
koji treba izbaciti da bi se isti balon podizao istom brzinom? Sila uzgona iznosi 1800 N.
A) 25 kg
B) 29 kg
C) 33 kg
D) 37 kg
E) 43 kg
rješenje: (C)
m=200 kg
F
u
=1800 N
Δ
m=?
m g
F
F
m
m g
F
F
F
mg
F
m
m g
F
mg
F
m
m g
F
mg
m
m
F
g
m
m
m
F
g
kg
N
ms
kg
u
tr
u
tr
tr
u
u
u
u
u
u
⋅ =
+
−
⋅ =
−
=
−
−
⋅ =
−
−
−
⋅ =
−
−
=
−
=
−
= ⋅
− ⋅
=
−
tijelo se spu{ta konstantnom brzinom
tijelo se penje konstantnom brzinom
uvrsti za
(
)
(
)
(
)
(
)
,
,
Δ
Δ
Δ
Δ
Δ
2
2
2
2
2 200
2 1800
9 81
33 02
2
305. Kolika je akceleracija sile teže na Marsu? Polumjer Zemlje ve
ć
i je 1,88 puta, a masa
Zemlje ve
ć
a je 9,1 puta od polumjera, odnosno mase Marsa.
A) 9,8 ms
-2
B) 3,8 ms
-2
C) 5,8 ms
-2
D) 15,1 ms
-2
E) 1,35 ms
-2
rješenje:
(B)
R
Z
=1,88 R
M
M
Z
=9,1 M
M
g
M
=?
g
G M
R
G
M
R
G M
R
g
ms
M
M
M
Z
Z
Z
Z
Z
=
⋅
=
⋅
⎛
⎝⎜
⎞
⎠⎟
=
⋅
⋅
=
⋅
=
−
2
2
2
2
2
2
9 1
1 88
1 88
9 1
1 88
9 1
3 81
,
,
,
,
,
,
,
306. Koliki naboj treba dati kugli mase 1 g da ona lebdi ispod drege kugle s nabojem
0,07·10
-6
C na udaljenosti 5 cm? (
ε
0
=8,85·10
-12
Fm
-1
)
A) -3,89·10
-8
C
B) 3,89·10
-4
C

196
rješenje:
(E)
r=53·10
-12
m
v=2,2·10
6
ms
-1
I=?
I
Q
t
Q
r
v
v Q
r
ms
C
m
A
I
mA
=
=
= ⋅ =
⋅
⋅
⋅
⋅ ⋅
⋅
=
=
−
−
−
−
2
2
2 2 10
1 6 10
2 53 10
3 14
0 00105
1
6
1
19
12
π
π
,
,
,
,
309. Molekula mase 3,35·10
-26
kg udara u stijenku posude brzinom 600 m/s. Pravac gibanja
molekule i stijenka posude zatvaraju kut 45°. Koliki je impuls sile primila stijenka posude?
A) 1,42·10
-21
Ns
B) 2,84·10
-23
Ns
C) 0
D) 5·10
-23
Ns
E) 10
-13
Ns
rješenje:
(B)
m=3,35·10
-26
kg
v=600 m/s
I=2 mv sin45°
α
=45°
I=2·3,35·10
-26
kg·600 ms
-1
·
√
2/2
I=?
I=2,84·10
-23
Ns
310. Za koliko
ć
e se pove
ć
ati volumen željezne kocke ako joj dovedemo toplinu od 296,4
kJ? (specifi
č
ni toplinski kapacitet željeza je 460 Jkg
-1
k
-1
, gusto
ć
a željeza je 7800 kgm
-3
i
linearni koeficijent toplinskog rastezanja željeza je 12·10
-6
K
-1
)
A) 2·10
-6
m
3
B) 1,5·10
-6
m
3
C) 4·10
-6
m
3
D) 5·10
-6
m
3
E) 3·10
-6
m
3
rješenje:
(E)
Q=296,4kJ
c=460Jkg
-1
K
-1
ρ
=7800kgm
-3
β
=12·10
-6
K
-1
Δ
V=?
Δ
Δ
Δ
Δ
Δ
Δ
Δ
Δ
Δ
V
V
t
V
t
t
V
V
Q
mc t
mc
V
V
c
V
V
Q
C
J
K
kgm
Jkg
K
m
= ⋅ ⋅ = ⋅ ⋅
⇒
=
⋅
=
=
⋅
⋅
= ⋅ ⋅
⇒
=
⋅
⋅
=
⋅
⋅ ⋅ ⋅
⋅
=
⋅
−
−
−
−
−
−
α
β
β
β
ρ
β
β
ρ
3
3
3
3
3
296 4 10
3 12 10
7800
460
2 96 10
3
6
1
3
1
1
6
3
,
,
311. Kada na oprugu objesimo masu 3 kg, njena duljina je 87,7 cm a za uteg 9 kg duljina je
142,7 cm. Koliki je period titranja kada na opruzi visi uteg od 5 kg?
A) 1,02 s
B) 2,2 s
C) 3 s
D) 1,36 s
E) 2,81 s
rješenje:
(D)
197
m
1
=3 kg
l
1
=87,7 cm
m
2
=9 kg
l
2
=142,7 cm
m=5 kg
T=?
k
F
x
m g
m g
l
l
kg
ms
m
Nm
T
m
k
kg
Nm
s
s
= =
−
−
=
⋅
−
⋅
=
=
=
=
=
−
−
−
−
2
1
2
1
2
2
1
1
6
9 81
142 7 87 7 10
107 01
2
2
5
107 01
1 357
1 36
,
(
,
, )
,
,
,
,
π
π
312. Neki ciklotron ima komoru maksimalnog radijusa 0,5 m, a magnetska indukcija iznosi
2 T. Kolika je najviša energija protona u tom ciklotronu? (M
p
=1,67·10
-27
kg, e=1,6·10
-19
c)
A) 13 eV
B) 17 J
C) 12 MeV
D) 48 MeV
E) 1 keV
rješenje: (D)
R=0,5 m
B=2 T
E=?
mv
R
Q v B
v
QBR
m
C
T
m
kg
ms
Ek
mv
kg
ms
J
Ek
eV
eV
MeV
2
19
27
8
1
2
27
8
1 2
11
11
19
8
1 6 10
2
0 5
1 67 10
0 958 10
2
1 6 10
0 958 10
2
0 766 10
0 766 10
1 6 10
0 47875 10
48
= ⋅ ⋅
⇒
=
=
⋅
⋅
⋅
⋅
=
⋅
=
=
⋅
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
=
−
−
−
−
−
−
−
−
,
,
,
,
,
( ,
)
,
,
,
,
313. Uteg privezan na nit duljine 30 cm opisuje u horizontalnoj ravnini kružnicu polumjera
15 cm. Koliki je period kruženja?
A) 58,5 min
B) 1,02 s
C) 2 s
-1
D) 0,543 s
-1
E) 5,43 s
-1
rješenje:
(B)
l=30 cm=0,3 m
R=15 cm=0,15 m
T=?

199
316. Dva šeta
č
a udaljeni su 150 m i hodaju jedan prema drugom. Prvi šeta
č
hoda brzi-nom
od 1 m/s, a drugi brzinom od 2 m/s. Na kojem djelu puta
ć
e se oni sresti, mjereno od prvog
šeta
č
a?
A) 100 m
B) 50 m
C) 130 m
D) 1 cm
E) 0,5 cm
rješenje: (B)
s=150 m
v
1
=1 ms
-1
v
2
=2 ms
-1
s
1
=?
s
s
s
s
v t
v t
t
s
v
v
m
ms
s
s
v
t
ms
s
m
=
+
=
+
=
+
=
=
=
⋅ =
⋅
=
−
−
1
2
1
2
1
2
1
1
1
1
150
3
50
1
50
50
317. Kolikom se najve
ć
om brzinom može gibati automobile po horizontalnoj cesti polu-
mjera zakrivljenosti 30 m da ne klizi, ako je faktor trenja izme
đ
u ceste i kota
č
a 0,25?
A) 8,6 m/s
B) 7,5 m/s
C) 50 km/h
D) 45 km/h
E) 9,7 m/s
rješenje:
(A)
R=30 m
μ
=0,25
v=?
F
F
mv
R
m g
v
g R
ms
m
ms
ms
c
tr
=
= ⋅ ⋅
⇒
=
⋅ ⋅ =
⋅
⋅
=
=
−
−
−
2
2
1
1
0 25 9 81
30
8 577
8 6
μ
μ
,
,
,
,
318. Raketa se podiže vertikalno u vis s ubrzanjem 4g. Koliko iznosi težina tijela mase m u
raketi?
A) 4 mg
B) 0
C) 5 mg
D) 2 mg
E) 1 mg
rješenje: (C)
a=4g
G=?
G=m·g+m·a=m·g+m·4g=5m·g
319.Tijelo iz mirovanja po
č
inje kliziti niz kosinu (
α
=5,7°) i prevalivši put od 100 m posti-
gne brzinu 5 m/s. Koliko se njegove potencijalne energije utroši na trenje i otpor zraka?
200
A) 33%
B) 85%
C) 99%
D) 87,2%
E) 10,4%
rješenje:
(D)
s=100 m
v=5 m/s
α
=5,7°
W
tr
/mgh=?
W
mgh
mgh
mv
mgh
mv
mgh
v
sg
W
mgh
m s
m
ms
tr
tr
=
−
= −
= −
⋅
= −
⋅
⋅
⋅
=
=
−
−
2
2
2
2
2
2
2
1
2
1
2
1
25
2 100
9 81
0 09927
0 8716
87 2%
sin
,
,
,
,
α
320. U kalorimetar je stavljeno 100 g neke teku
ć
ine. U nju je uronjen grija
č
kojim te
ć
e
struja 0,5 A. Otpor grija
č
a je 50
Ω
. Ako je grija
č
uklju
č
en dvije minute, temperatura teku
ć
i-
ne se pove
ć
a za 7 K. Koliki je specifi
č
ni toplinski kapacitet teku
ć
ine?
A) 6,5 kJkg
-1
K
-1
B) 7·10
3
Jkg
-1
K
-1
C) 8,14·10
3
Jkg
-1
K
-1
D) 9,2 kJkg
-1
K
-1
E) 2,14·10
3
Jkg
-1
K
-1
rješenje: (E)
m=100 g=0,1 kg
I=0,5 A
R=50
Ω
t=2 min=120 s
Δ
t=7 K
c=?
W
Q
UIt
mc t
U
I R
I Rt
mc t
c
I Rt
m t
A
s
kg
K
Jkg
K
=
=
= ⋅
=
=
=
⋅
⋅
⋅
=
⋅
−
−
Δ
Δ
Δ
Ω
2
2
2
2
3
1
1
0 5
50
120
0 1
7
2 14285 10
,
,
,
321. Djevoj
č
ica se ljulja na ljulja
č
ki. Najviša to
č
ka iznad tla do koje se pri tom podigne jest
2,5 m, a najniža 1 m. Kolika je njena maksimalna brzina?
A) 3,4 m/s
B) 7,2 m/s
C) 7,1 m/s
D) 5,4 m/s
E) 6,2 m/s
rješenje:
(D)
h
1
=2,5 m
h
2
=1 m
v
max
=?
Δ
Δ
h
h
h
m
m
m
v
g h
ms
m
ms
=
−
=
−
=
=
=
⋅
⋅
=
−
−
1
2
2
1
2 5
1 0
1 5
2
2 9 81
1 5
5 42
,
,
,
,
,
,
322. Kondenzator ima kapacitivni otpor 40
Ω
pri frekvenciji struje od 50 Hz. Za koliko
postotaka treba promijeniti frekvenciju da bi se kapacitivni otpor pove
ć
ao za 20%?

202
324. Dva tijela, jedno mase m
1
=8 kg i drugo mase m
2
=2 kg leže jedno pokraj drugog na
glatkoj površini. Tijelo mase m
1
ubrzava se silom F
1
=0,7 N, a tijelo mase m
2
silom F
2
=1,4
N, u istom smjeru. Oba se tijela po
č
inju ubrzavati u istom trenutku. Nakon kojeg
ć
e se
vremena pre
đ
eni putovi razlikovati za 5 m?
A) 3,03 s
B) 2,02 s
C) 6,06 s
D) 5,05 s
E) 4,04 s
rješenje:
E)
m
1
=8 kg
m
2
=2 kg
F
1
=0,7 N
F
2
=1,4 N
Δ
s=5 m
t=?
a
F
m
N
kg
ms
a
F
m
N
kg
ms
s
s
a t
a t
m
t
t
ms
t
s
t
s
t
s
1
1
1
2
2
2
2
2
2
1
2
2
1
2
2
2
2
2
2
2
2
0 7
8
0 0875
1 4
2
0 7
2
2
5
0 7
2
0 0875
2
0 6125
10
16 32
4 04
=
=
=
=
=
=
−
=
−
=
−
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
=
=
=
−
−
−
,
,
,
,
,
,
,
,
,
325. Pet
č
lanaka, svaki elektromotorne sile 1,5 V i unutrašnjeg otpora 0,5
Ω
spojeni su
paralelno u bateriju i priklju
č
eni na vanjski otpor. Kolika je snaga na vanjskom otporu ako
kroz njega te
č
e struja jakosti 2 A?
A) 0,5 W
B) 3,6 W
C) 2,6 W
D) 1,5 W
E) 1,8 W
rješenje:
(C)
E=1,5 V
R
u
=0,5
Ω
n=5
P=?
I
E
R
n
R
R
E
I
R
n
V
A
P
U I
U
I R
P
I R
A
W
u
v
v
u
v
=
+
= −
=
−
=
−
=
= ⋅
= ⋅
=
=
⋅
=
1 5
2
0 5
5
0 75
0 1
0 65
2
0 65
2 6
2
2
,
,
,
,
,
(
)
,
,
Ω
Ω
Ω
Ω
Ω
203
326. Zvuk
č
ija je valna duljina u zraku 77 cm prelazi iz zraka u vodu. Kolika je valna
duljina u vodi? Brzina valova zvuka u zraku je 340 m/s, a u vodi 1500 m/s.
A) 340 cm
B) 77 cm
C) 1500 cm
D) 240 cm
E) 144 cm
rješenje:
(A)
λ
1
=77 cm=0,77 m
v
1
=340 m/s
v
2
=1500 m/s
λ
2
=?
f
v
ms
m
Hz
v
f
ms
Hz
m
cm
cm
1
1
1
1
2
2
1
1
340
0 77
441 55
1500
441 55
3 397
339 7
340
=
=
=
=
=
=
=
=
−
−
λ
λ
,
,
,
,
,
327. S visine 100 m iznad tla ba
č
en je kamen vertikalno prema dolje po
č
etnom brzi-nom 5
m/s. Kojom po
č
etnom brzinom treba istovremeno baciti drugi kamen s tla verti-kalno u vis
da bi se oni sudarili na pola puta?
A) 2,72 m/s
B) 31,72 m/s
C) 19,62 m/s
D) 63,42 m/s
E) 5 m/s
rješenje:
(B)
s=100 m
v
0
=5 ms
-1
v
01
=?
v t
gt
t
t
t
t
s
t
s
0
2
2
1 2
2
1 2
1
2
50
5
4 905
50
0
4 905
4 905
20 50
10
4 905 32
10
2 709
+
=
+
−
=
=
−
±
+
⋅
= −
±
=
,
,
,
,
,
,
,
v t
gt
v t
m
v t
m
v
m
s
v
ms
01
2
01
2
01
01
01
1
2
50
50
9 81 2 709
2
50
35 996
50
35 996
2 709
31 74
−
=
=
+
⋅
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
=
+
=
+
=
−
,
,
(
,
)
,
,
,
328. U cilindri
č
ku posudu visine 20 cm nalijemo do polovice živu, a zatim do vrha vodu.
Koliki tlak na dno posude uzrokuju te dvije teku
ć
ine? (gusto
ć
a žive je 13600 kg/m
3
)
A) 0,143 bar
B) 0,5 bar
C) 0,3 bar
D) 0,01 bar
E) 1,013 bar
rješenje:
(A)

205
331. Nabijena metalna kugla obješena na izoliranoj niti stavi se u homogeno vodoravno
elektri
č
no polje i pritom nit zatvara kut 45° s vertikalom. Ako se kugli oduzme 1/5 njezinog
naboja, za koliko se onda otkloni kuglica?
A) 38,66°
B) 30°
C) 45°
D) 43,22°
E) 51,13°
rješenje: (A)
α
=45°
Q
2
=4/5Q
α
2
=?
tg
F
Q
E Q
G
tg
E
Q
G
tg
tg
α
α
α
α
=
= ⋅
=
⋅
=
=
= =
=
2
2
4
5
4
5
4
5
45
4
5
0 8
38 66
o
o
,
,
332. U kondenzatoru elektronske bljeskalice fotografskog aparata
č
iji je kapacitet 100
μ
F
pohranjena je energija od 50 J. Koliki naboj pro
đ
e kroz bljeskalicu ako se kroz nju konden-
zator potpuno isprazni?
A) 0,15 C
B) 0,02 C
C) 0,04 C
D) 0,2 C
E) 0,01 C
rješenje:
(E)
W=50 J
C=100
μ
F
Q=?
W
CU
ako je
U
Q
C
W
C
Q
C
Q
C
Q
WC
J
F
C
=
=
=
⋅
=
=
= ⋅
⋅
⋅
=
−
1
2
1
2
1
2
2
2 50 100 10
0 01
2
2
2
6
,
333. Gibaju
ć
i se brzinom 12 km/h vagon mase 50 tona nalije
ć
e na mirni vagon mase 30
tona. Sudar vagona je savršeno neelasti
č
an. Na kojoj
ć
e se udaljenosti vagoni zaustaviti ako
je faktor trenja izme
đ
u vagona i tra
č
nica 0,05?
A) 4,4 m
B) 2,7 m
C) 16 m
206
D) 3,2 m
E) 7 m
rješenje:
(A)
v
1
=12 km/h
m
1
=50 t
v
2
=0
m
2
=30 t
m=0,05
s=?
m v
m v
m
m
v
v
m v
m v
m
m
t
kmh
t
kmh
t
ms
F
m g
m a
a
g
s
v
a
v
g
ms
ms
m
1 1
2
2
1
2
1 1
2
2
1
2
1
1
1
2
2
1 2
2
50 12
30 0
80
2 08
2
2
2 08
2 0 05 9 81
4 4
+
=
+
⋅
=
+
+
=
⋅
+
⋅
=
= ⋅ ⋅ = ⋅
= ⋅
=
=
⋅
=
⋅
⋅
=
−
−
−
−
−
(
)
,
( ,
)
,
,
,
μ
μ
μ
334. Zraka svjetlosti pada na granicu dvaju sredstava pod kutom od 30° u odnosu na
okomicu. Indeks loma prvog sredstva je 2,6. Koliki je indeks loma drugog sredstva ako su
reflektirana i lomljena zraka me
đ
usobno pod pravim kutom?
A) 2,6
B) 3
C) 0,66
D) 0,75
E) 1,5
rješenje:
(E)
n
1
=2,6
α
=30°
n
2
=?
n
v
v
v
v
v
v
n
v
v
v
v
1
1
2
1
2
1
2
2
1
3
2
2
2 6
2 6
2 6
3
1 5
=
=
=
=
=
⋅
=
,
,
,
,
n
v
v
l
u
v
v
v
v
2
3
3
2
3
2
3
2
3
2
1
2
3
3
=
=
=
=
=
⋅
sin
sin
335. Tijelo mase 1 kg je ba
č
eno s visine 20 m po
č
etnom brzinom 10 m/s. Kolika je kineti-
č
ka energija tijela na visini od 10 m? (g=10 m/s
2
).
A) 50 J
B) 100 J
C) 150 J
D) 200 J
E) 250 J

208
338. Koliko fotona valne duljine 663 nm bi trebalo u sekundi poga
đ
ati u okomitom smjeru
savršeno reflektiraju
ć
u plo
č
u da bi sila na plo
č
u iznosila 1 N? (h=6,63·10
-34
Js)
A) 5·27
27
/s
B) 2,5·10
26
/s
C) 3,5·10
26
/s
D) 5·10
26
/s
E) 1·10
26
/s
rješenje:
(D)
λ
=663 nm
F=1 N
t=1 s
n=?
F t
m c
F t
nh
n
F t
h
n
N
s
m
Js
n
s
⋅ = ⋅
⋅ =
= ⋅ ⋅
=
⋅ ⋅
⋅
⋅
⋅
= ⋅
−
−
−
2
2
1
1 663 10
2 6 63 10
5 10
9
34
26
1
λ
λ
,
E
E
mc
n h c
m c
c
n h c
m c
n h c
c
k
f
=
= ⋅ ⋅
⋅ ⋅ = ⋅ ⋅
⋅ = ⋅ ⋅ ⋅ /
⋅ /
2
2
2
2
λ
λ
λ
339. Kompresor, koji ima volumen 4 dm
3
, usisava zrak pri temperaturi -3 °C i tlak 10
5
Pa.
Koliko hodova treba napraviti klip da bi zrak u spremniku volumena 1,5 m
3
poprimio
temperaturu 45 °C i tlak 2·10
5
Pa? (Smatrati da je prije po
č
etka punjenja u spremniku bio
vakuum)
A) 637
B) 754
C) 245
D) 678
E) 834
rješenje:
(A)
p
1
=10
5
Pa
V
1
=4 dm
3
=4·10
-3
m
3
T
1
=270 K
V
2
=1,5 m
3
p
2
=2·10
5
Pa
T
2
=273+45=318 K
n=?
n
p V
T
p V
T
n
p V
T
p V T
Pa
m
K
Pa
m
K
⋅
=
=
⋅
⋅
=
⋅
⋅
⋅
⋅ ⋅
⋅
=
=
−
1
1
1
2
2
2
2
2
1
1
1
2
5
3
5
3
3
2 10
1 5
270
10
4 10
318
636 7
637
,
,
340. Na oprugu konstante elasti
č
nosti 10 N/m, koja slobodno visi, objesimo uteg mase 0,1
kg i pustimo da titra. Kolika
ć
e biti maksimalna brzina utega?
A) 1,38 m/s

211
rješenje:
(B)
T
1
=2s
β
=0,9·10
-5
K
-1
t
0
=0° C
t=30° C
Δ
t=?
l
l
t
l
K
K
l
T
T
l
g
l
g
T
T s
T
T s
t
s
s
s
s
s
=
+
=
+
⋅
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
−
=
−
=
−
−
0
0
5
1
0
2
1
0
0
2
2
1
2 2
2
1
1
1 0 9 10
30
1 00027
2
1 00027
2
1 00027
1 0001349
86400
86400
1 0001349
86400
86388 346
11 654
(
)
(
,
)
,
,
,
,
,
,
,
βΔ
π
π
Δ
346. Koliko iznosi masa bakrene žice gusto
ć
e 8,9·10
3
kgm
-3
promjera 2 mm i otpornosti
1,72·10
-6
Ω
m, ako je otpor žice 5
Ω
?
A) 2 kg
B) 1 kg
C) 0,91 kg
D) 255 g
E) 0,15 kg
rješenje:
(D)
d=8,9·10
3
kgm
-3
2r=2 mm
ρ
=1,72·10
-6
Ω
m
R=5
Ω
m=?
R
l
S
l
R S
m
m
m
m
V d
r
l d
m
m
kgm
m
kg
g
=
⋅
= ⋅ =
⋅
⋅
⋅
=
= ⋅ =
⋅ ⋅ =
⋅
⋅
⋅
⋅
=
⋅
=
−
−
−
−
−
ρ
ρ
π
5
10
3 14
1 72 10
9 1279
10
3 14 9 1279
8 9 10
255 10
255
3 2
2
6
2
3 2
2
3
3
3
Ω
Ω
(
)
,
,
,
(
)
,
,
,
347. Koliki mora biti otpor žice elektri
č
nog kuhala s kojim se litra vode temperature 20 °C
može za 8 minuta dovesti do vrenja? Kuhalo je priklju
č
eno na 220 V, a toplinski kapacitet
vode iznosi 4,186 kJkg
-1
K
-1
. Zanemariti otpor dovodnih žica.
A) 69,4
Ω
B) 2,0
Ω
C) 50,1
Ω
D) 3,5
Ω
E) 10,3
Ω
rješenje:
(A)
212
m=1 kg
t
1
=20 °C
t
2
=100 °C
t=8 min
U=220 V
U I t
Q I
U
R
U
t
R
Q
⋅ ⋅ =
=
⋅ =
2
c=4,186 kJkg
-1
K
-1
R=?
R
U
t
mc t
V
s
kg
Jkg
K
K
=
⋅ =
⋅ ⋅
⋅
⋅
⋅
=
−
−
2
2
2
3
1
1
220
8 60
1
4 186 10
80
69 37
Δ
Ω
,
,
348. Ako je relativni indeks loma zrak-staklo 1,5, a zrak-voda 1,33, izra
č
unati relativni
indeks loma voda-staklo.
A) 1,13
B) 2,01
C) 0,7
D) 1,56
E) 1,46
rješenje:
(A)
n
z/s
=1,5
n
z/v
=1,33
n
v/s
=?
n
c
c
c
n
c
n
c
c
c
n
c
n
c
c
n
c
n
c
z
s
s
z
s
z
s
z
z
v
v
s
v
z
v
z
v
s
s
v
z
s
z
z
v
z
=
⇒
=
⋅
=
⇒
=
⋅
=
=
⋅ /
⋅ /
=
=
=
1 5
1 33
1 1278
1 13
,
,
,
,
______________________________________________________________________

2
ZADATCI
(Broj zadatka odgovara broju rješenja)
1
. Autobus kreće sa stanice i jednoliko ubrzava po ravnoj cesti, zatim vozi stalnom brzinom te se
zaustavi pred semaforom. Koji od prikazanih grafova ovisnosti poloţaja o vremenu opisuje gibanje
autobusa?
2.
Gibanje nekoga tijela opisano je (
v,t
) grafom koji je prikazan crteţom.
Srednja brzina tijela u vremenu od 8 sekundi iznosi:
A.
1,0 m s
−1
B.
4,5 m s
−1
C.
5,0 m s
−1
D.
5,5 m s
−1
3
. Tijelo se giba jednoliko po kruţnici. Kakva je njegova brzina?
A.
stalna po iznosu i smjeru
B.
stalna po iznosu i promjenjiva po smjeru
C.
promjenjiva po iznosu i stalna po smjeru
D.
promjenjiva po iznosu i smjeru
4.
Tijelo je izbačeno horizontalno blizu površine Zemlje. Otpor zraka je zanemariv. Koja od navedenih
veličina
nije
stalna pri gibanju tijela?
A.
horizontalna komponenta brzine
B.
vertikalna komponenta brzine
C.
horizontalna komponenta ubrzanja
D.
vertikalna komponenta ubrzanja
5.
Dvoja se kolica gibaju ususret jedna drugima. Nakon savršeno neelastičnoga centralnoga sudara,
oboja kolica ostanu mirovati na mjestu sudara. Iz toga moţemo zaključiti da su prije sudara kolica
imala jednake iznose:
A.
brzina
B.
masa
C.
kinetičkih energija
D.
količina gibanja
A
D
C
B
G
F
3
6.
Učenici su izmjerili visinu nekoga predmeta pet puta i dobili ove vrijednosti: 11,25 cm, 11,20 cm,
11,22 cm, 11,18 cm i 11,25 cm. Što se moţe zaključiti o visini
h
toga predmeta?
A.
h
= (11,22 ± 0,03) cm
B.
h
= (11,22 ± 0,04) cm
C.
h
= (11,25 ± 0,07) cm
D.
h
= (11,25 ± 0,03) cm
7.
Knjiga mase 2 kg miruje na horizontalnome stolu. Koliki je iznos sile kojom stol djeluje na knjigu?
A.
0 N
B.
2 N
C.
10 N
D.
20 N
8.
Tijela A i B privlače se gravitacijskom silom. Kad bi tijelo B imalo devet puta manju masu, koliki
bi trebao biti razmak meĎu tijelima A i B da bi gravitacijska sila meĎu njima ostala ista?
A.
tri puta manji
B.
devet puta manji
C.
tri puta veći
D.
devet puta veći
9.
Koji od četiriju prikazanih dijagrama predstavlja izohorni proces?
10.
Temperatura neke količine idealnoga plina poveća se četiri puta pri čemu mu se volumen poveća
dva puta. Tlak toga plina se pritom:
A.
smanji dva puta
B.
smanji četiri puta
C.
poveća dva puta
D
. poveća četiri puta
11.
Plin je podvrgnut procesu promjene stanja pri kojem se ne obavlja rad. Koji je to proces?
A.
izobarni
B.
adijabatski
C.
izotermni
D.
izohorni
12.
Čemu je od navedenoga proporcionalna temperatura idealnoga plina?
A.
srednjoj potencijalnoj energiji čestica plina
B.
srednjoj kinetičkoj energiji nasumičnoga gibanja čestica plina
C.
srednjoj brzini nasumičnoga gibanja čestica plina
D.
srednjoj akceleraciji nasumičnoga gibanja čestica plina

5
A.
0 mT
B.
1 mT
C.
2 mT
D.
4 mT
19.
Koja je mjerna jedinica za električnu otpornost?
A.
Ω
B.
Ω m
C.
Ω/m
D.
Ω
20.
Električni titrajni krug sastoji se od zavojnice induktiviteta 2 mH i kondenzatora kapaciteta 80 μF.
Koliko iznosi vlastita frekvencija toga titrajnoga kruga?
A.
99 Hz
B.
398 Hz
C.
1 254 Hz
D.
2 500 Hz
21.
Na crteţu su prikazana četiri njihala koja vise na vodoravnoj šipci. Po dva njihala su jednakih
duljina: njihala K i N duţa su od njihala L i M. Utezi od 10 dag ovješeni su na njihala K i L, a utezi od
5 dag na njihala M i N.
Mjerenjem trebate otkriti kako duljina njihala utječe na period njihanja. Za mjerenje je dovoljno rabiti
samo dva njihala. Koja dva njihala trebate uporabiti da to otkrijete?
A.
K i L
B.
L i M
C.
L i N
D.
K i N
22.
Otpornik i zavojnica spojeni su serijski na izvor izmjeničnoga napona. Ako se frekvencija napona
smanji, što će se dogoditi s ukupnim otporom kruga?
A.
Smanjit će se.
B.
Ostat će nepromijenjen.
C.
Povećat će se.
6
23.
Elektroskop je negativno nabijen zbog čega je kazaljka elektroskopa otklonjena za neki kut. Ako
se elektroskopu pribliţi negativno nabijeni štap (bez doticanja), što će se dogoditi s kutom otklona
kazaljke elektroskopa?
A.
Smanjit će se.
B.
Ostat će nepromijenjen.
C.
Povećat će se.
24.
Uteg je ovješen na elastičnu oprugu. Što će se dogoditi s periodom titranja ako na oprugu ovjesimo
još jedan uteg?
A.
Smanjit će se.
B.
Ostat će nepromijenjen.
C.
Povećat će se.
25.
Automobil vozi brzinom 20 m/s u vodoravno poloţenome zavoju polumjera zakrivljenosti 80 m.
Koliki mora biti najmanji faktor trenja izmeĎu guma i ceste da bi vozilo prošlo zavoj sa stalnim
iznosom brzine?
25.
Automobil vozi brzinom 20 m/s u vodoravno poloţenome zavoju polumjera zakrivljenosti 80 m.
Koliki mora biti najmanji faktor trenja izmeĎu guma i ceste da bi vozilo prošlo zavoj sa stalnim
iznosom brzine?
27.
Za pripremu tople kupke temperature 35 ºC u 60 kg hladne vode temperature 20 ºC dodamo vruću
vodu temperature 80 ºC. Kolika je masa vruće vode koju smo dodali?
28.
Vodič duljine 1 m giba se u homogenome magnetskome polju iznosa 0,1 T okomito na silnice
polja. Brzina vodiča iznosi 2 m/s. Koliki se napon inducira na krajevima toga vodiča?
29.
Na nekome električnome ureĎaju stoje oznake 220 V, 50 W. Koliki je otpor toga ureĎaja?
30.
Elastičnu zavojnicu na koju je ovješen uteg izvučemo iz poloţaja ravnoteţe za 2 cm i pustimo
titrati. Konstanta elastičnosti zavojnice iznosi 1 000 N
. Nakon nekoga vremena zavojnica prestane
titrati. Koliko je energije zavojnica predala okolini tijekom titranja?
31.
Komad pluta obujma 500 c
pliva na vodi. Pluto pritisnemo rukom tako da ono potpuno uroni u
vodu. Gustoća pluta iznosi 300 kg
, a vode 1 000 kg
.
31.1.
Kolikom silom uzgona djeluje voda na pluto kada je pluto potpuno uronjeno u vodu?
31.2.
Kolikom silom trebamo djelovati na pluto da bi ono mirovalo ispod površine vode?
32.
Kutija mase 1 kg giba se niz kosinu nagiba 30º. Trenje je zanemarivo.
32.1.
Koliko iznosi ubrzanje kutije?
32.2.
Kolikom silom kutija pritišće podlogu?
33.
Zgrada od opeke ima visinu 20 m po zimi pri temperaturi od −10 ºC. Koeficijent linearnoga
rastezanja opeke iznosi 1
.
33.1.
Kolika je visina zgrade pri temperaturi od 0 ºC?
33.2.
Za koliko će se promijeniti visina zgrade od zime do ljeta kad temperatura iznosi 25 ºC?

8
40.
Na termometru je očitana temperatura zraka od 290 K. Kolika je temperatura zraka u Celzijusevim
stupnjevima?
A.
15 °C
B.
17 °C
C.
19 °C
D.
21 °C
41.
Koja od navedenih tvrdnji
ne vrijedi
za model idealnoga plina?
A.
Kinetička energija nasumičnoga gibanja čestica plina manja je od potencijalne energije njihova
meĎusobnoga djelovanja.
B.
Čestice plina se stalno nasumično gibaju.
C.
Sudari čestica plina sa stijenkama posude su savršeno elastični.
D.
Temperatura plina proporcionalna je srednjoj kinetičkoj energiji nasumičnoga gibanja čestica plina.
42.
Temperatura idealnoga plina je 0 °C. Na kojoj će temperaturi tlak plina biti dva puta veći od tlaka
plina pri 0 °C ako se obujam plina drţi stalnim?
A.
0 K
B.
137 K
C.
273 K
D.
546 K
43.
Dvije jednake metalne kugle prikazane na slici vise na nitima od izolatora. Obje kugle su početno
električki neutralne. Kugla M nabije se negativno nabojem od −6 nC i zatim se dotakne kuglom N.
Koliko će nakon toga iznositi naboj na kugli N?
A.
−6 nC
B.
−3 nC
C.
+3 nC
D.
+6 nC
44.
U strujnome krugu prikazanome na slici ampermetar pokazuje 2 A. Unutrašnji otpor baterije je
zanemariv.
Koliki napon pokazuje voltmetar uz uvjet da su instrumenti idealni?
A.
4 V
B.
6 V
C.
8 V
D.
12 V
9
45.
Vodičem teče struja od 0,5 mA. Koliko elektrona proĎe poprečnim presjekom vodiča za 0,1 s?
A.
0,5·10
14
B.
3,125·10
14
C.
3,125·10
17
D.
3,125·10
19
46.
Na slici su prikazane silnice električnoga polja.
Koji odnos vrijedi za iznose električnoga polja u označenim točkama 1, 2 i 3?
A.
E3 > E2 > E1
B.
E2 > E1 > E3
C.
E1 > E3 > E2
D.
E3 > E1 > E2
47.
Na udaljenosti 2 m od ravnoga vodiča kojim teče stalna struja magnetsko polje iznosi 4 mT.
Koliko će iznositi magnetsko polje na udaljenosti 1 m od toga vodiča?
A.
2 mT
B.
4 mT
C.
8 mT
D.
16 mT
48.
Konvergentna leća ima ţarišnu daljinu
f
. Kakva slika nastane kada je udaljenost predmeta od leće
manja od
f
?
A.
realna i uvećana
B.
realna i umanjena
C.
virtualna i uvećana
D.
virtualna i umanjena
49.
Na optičku rešetku okomito upada monokromatska svjetlost valne duljine 400 nm. Sinus ogibnoga
kuta za prvi maksimum iznosi 0,2. Kolika je konstanta optičke rešetke?
A.
1
μ
m
B.
2
μ
m
C.
3
μ
m
D.
4
μ
m
50.
Na grafu je prikazano kako elongacija tijela koje titra ovisi o vremenu.

11
56.
Foton energije 3,27 eV izazove fotoelektrični učinak na nekome metalu. Izlazni rad fotoelektrona
za taj metal je 2,08 eV. Kolika je kinetička energija fotoelektrona?
A.
1,19 eV
B.
2,08 eV
C.
3,27 eV
D.
5,35 eV
57.
Jabuka pada na Zemlju zbog gravitacijskoga privlačenja izmeĎu nje i Zemlje. Označi li se sila
kojom Zemlja privlači jabuku s
F
1
, a sila kojom jabuka privlači Zemlju s
F
2
, u kakvome su odnosu
iznosi tih dviju sila?
A.
F
1
<
F
2
B.
F
1
=
F
2
C.
F
1
>
F
2
58.
Tijelo A slobodno pada s visine
h
, a tijelo B je s iste visine
h
izbačeno u vodoravnome smjeru.
Kako se odnose vrijeme gibanja tijela A (
t
A
) i vrijeme gibanja tijela B (
t
B
) do trenutka pada?
A.
t
A
<
t
B
B.
t
A
=
t
B
C.
t
A
>
t
B
59.
De Broglieve valne duljine elektrona i protona bit će jednake kada elektron i proton imaju jednake:
A.
količine gibanja
B.
kinetičke energije
C.
brzine
60.
Tijelo mase 10 kg pada s visine 80 m i pri udarcu o površinu Zemlje ima kinetičku energiju 4500 J.
Koliko je energije tijelo utrošilo na savladavanje otpora zraka?
2616.
Kolikom silom Mars privlači kamen mase 1 kg koji se nalazi na njegovoj površini? Masa Marsa
je
kg, a polumjer 3400 km.
62.
Pri stalnome tlaku od
Pa plin obavi rad od 1000 J. Za koliko se povećao obujam plina?
63.
Krug izmjenične struje sastavljen je od zavojnice zanemarivoga omskoga otpora i induktivnoga
otpora 600 te kondenzatora kapacitivnoga otpora 200 . Koliko iznosi impedancija ovoga strujnoga
kruga?
64.
U radioprijamniku se ugaĎanje frekvencije prijama ostvaruje pomoću LC kruga u kojem su serijski
spojeni zavojnica induktiviteta 0,8 μH i kondenzator promjenljivoga kapaciteta. Uz koju će se
vrijednost kapaciteta moći primati program stanice koja emitira na 95 MHz?
65.
Vlastito vrijeme ţivota neke čestice iznosi
T
0
. Kolika treba biti brzina čestice u laboratorijskome
sustavu da za promatrača u tome sustavu njezino vrijeme ţivota iznosi 2
T
0
?
12
66.
Sustav prikazan na slici sastoji se od jednoga koloturnika zanemarive mase i dvaju tijela. Trenje
niti s koloturnikom moţe se zanemariti. Tijela se gibaju akceleracijom od
. Sila trenja izmeĎu
stola i tijela mase
iznosi 5 N. Koliko iznosi masa
?
67.
Voda se zagrijava u aluminijskome loncu uz stalno miješanje. Početno su voda i lonac na
temperaturi od 20 °C. Nakon što zajedno prime 175,2 kJ topline, temperatura vode i lonca poveća se
na 60 °C. Ako je masa vode 1 kg, masa lonca 0,2 kg, a specifični toplinski kapacitet vode 4200
J kg
–1
K
–1
, koliki je specifični toplinski kapacitet aluminija?
68.
Na slici je prikazan bakreni štap duljine 80 cm koji leţi u magnetskome polju iznosa 5 mT. Štap se
jednoliko pomiče okomito na silnice polja brzinom 20 m s
–1
.
33.1.
Koliki se napon inducira izmeĎu krajeva štapa?
33.2.
Na slici označite na kojem je kraju štapa + pol, a na kojem – pol.
69.
Učenici su četiri puta mjerili valnu duljinu svjetlosti pomoću interferencije svjetlosti na dvjema
pukotinama i dobili sljedeće vrijednosti za isti izvor:
Koji je rezultat njihova mjerenja zajedno s pripadnom maksimalnom apsolutnom pogrješkom?
70.
Neko apsolutno crno tijelo zrači najviše energije na valnoj duljini od
. Kolika je snaga
zračenja toga tijela ako mu površina iznosi 0,1
?
71.
Slika prikazuje graf ubrzanja nekoga tijela u ovisnosti o vremenu. Tijelo se giba duţ
x
-osi. U
trenutku
t
= 0 s tijelo ima brzinu
v
0
= 0 m s
–1
.

14
77.
Temperatura idealnoga plina je 0 °C. Na kojoj će temperaturi obujam plina biti dva puta veći od
obujma plina pri 0 °C ako se tlak plina drţi stalnim?
A.
0 K
B.
137 K
C.
273 K
D.
546 K
78.
Dvije jednake metalne kugle prikazane na slici vise na nitima od izolatora. Obje kugle su početno
električki neutralne. Kugla M nabije se pozitivno nabojem od +8 nC i zatim se dotakne kuglom N.
Koliko će nakon toga iznositi naboj na kugli N?
A.
−8 nC
B.
−4 nC
C.
+4 nC
D.
+8 nC
79.
U strujnome krugu prikazanome na slici voltmetar pokazuje 4 V. Unutrašnji otpor baterije je
zanemariv.
Koliku jakost struje pokazuje ampermetar uz uvjet da su instrumenti idealni?
A.
1 A
B.
2 A
C.
3 A
D.
4 A
80.
Poprečnim presjekom vodiča za 0,1 s proteče
elektrona. Kolika je jakost struje koja
teče vodičem?
A.
0,5 mA
B.
5 mA
C.
0,5 A
D.
5 A
81.
Na slici su prikazane silnice električnoga polja i tri točke u tom polju označene brojevima 1, 2 i 3.
Postavimo li proton u točku 1, polje će na njega djelovati silom , u točki 2 će na proton djelovati sila
, a u točki 3 sila .
Koji odnos vrijedi za iznose spomenutih sila?
A.
>
>
15
B.
>
>
C.
>
>
D.
>
>
82.
Na udaljenosti 2 m od ravnoga vodiča kojim teče stalna struja magnetsko polje iznosi 2 mT. Na
kolikoj udaljenosti od toga vodiča magnetsko polje iznosi 4 mT?
A.
1 m
B.
2 m
C.
4 m
D.
8 m
83.
Konvergentna leća ima ţarišnu daljinu
f
. Kakva slika nastane kada je udaljenost predmeta od leće
veća od
f
, a manja od 2
f
?
A.
realna i obrnuta
B.
realna i uspravna
C.
virtualna i uspravna
D.
virtualna i obrnuta
84.
Na optičkoj rešetki ogiba se bijela svjetlost. Koje je boje svjetlost koja se ogiba pod najmanjim
ogibnim kutom ako se promatra spektar prvoga reda?
A.
crvene
B.
ljubičaste
C.
zelene
D.
ţute
85.
Na grafu je prikazano kako elongacija tijela koje titra ovisi o vremenu.
Koliki je period titranja tijela?
A.
2 s
B.
4 s
C.
6 s
D.
8 s
86.
Val prelazi iz sredstva A u sredstvo B. U sredstvu A brzina vala iznosi 100 m
–
, a valna duljina
0,5 m. U sredstvu B se brzina vala poveća na 160 m
–
. Kolika je valna duljina vala u sredstvu B?
A.
0,5 m
B.
0,8 m
C.
100 m
D.
160 m

17
94.
Elektron i proton imaju jednake količine gibanja. Što im je još jednako?
A.
de Broglieve valne duljine
B.
kinetičke energije
C.
brzine
95.
Tijelo mase 10 kg pada s neke visine i pri udarcu o površinu Zemlje ima kinetičku energiju 4500J.
S koje je visine tijelo počelo padati ako je na savladavanje sile otpora zraka utrošilo 3500 J svoje
energije?
96.
Masa Marsa je 6,5·1
kg, a polumjer 3400 km. Kolika je akceleracija slobodnoga pada na
površini Marsa?
97.
Pri stalnome tlaku od 2·1
Pa na plinu se obavi rad od 1000 J. Za koliko se smanjio obujam
plina?
98.
Krug izmjenične struje sastavljen je od serijskoga spoja otpornika omskoga otpora 300 i
kondenzatora kapacitivnoga otpora 400 . Koliko iznosi impedancija ovoga strujnoga kruga?
99.
U radioprijamniku se ugaĎanje frekvencije prijama ostvaruje pomoću LC kruga u kojem je spojena
zavojnica induktiviteta 0,6 μH i kondenzator promjenljivoga kapaciteta. Na kojoj će se frekvenciji
moći primati program tim prijamnikom ako se vrijednost kapaciteta postavi na 3,5 pF?
100.
Vlastito vrijeme ţivota neke čestice iznosi
T
0
= 2
µ
s. Koliko iznosi njezino vrijeme ţivota u
laboratorijskome sustavu u kojem se čestica giba brzinom 0,6
c
?
101.
Sustav prikazan na slici sastoji se od jednoga koloturnika zanemarive mase i dvaju tijela. Trenje
izmeĎu tijela mase
m
2
i stola, kao i trenje izmeĎu niti i koloturnika mogu se zanemariti. Koliko iznosi
akceleracija kojom se gibaju ova tijela?
102.
Voda se zagrijava u aluminijskome loncu uz stalno miješanje. Početno su voda i lonac na
temperaturi od 20 °C. Nakon što su zajedno primili 91,2 kJ topline, temperatura vode i lonca povećala
se na 60 °C. Odredite masu vode ako je masa lonca 0,2 kg, specifični toplinski kapacitet vode 4200
J kg
–1
K
–1
, a specifični toplinski kapacitet aluminija 900 J kg
–1
K
–1
.
103.
Na slici je prikazan bakreni štap koji leţi u magnetskome polju iznosa 5 mT. Štap se jednoliko
pomiče okomito na silnice polja brzinom 20 m
. Pritom se izmeĎu krajeva štapa inducira napon od
0,08 V.
18
33.1.
Kolika je duljina štapa?
33.2.
Na slici označite na kojem je kraju štapa + pol, a na kojem – pol.
104.
Učenici su u pokusu s interferencijom svjetlosti na dvjema pukotinama četiri puta mjerili razmak
izmeĎu susjednih interferentnih pruga i dobili sljedeće vrijednosti:
Koji je rezultat njihova mjerenja s pripadnom maksimalnom apsolutnom pogrješkom?
105.
Neko apsolutno crno tijelo zrači najviše energije na valnoj duljini od
m. Kolika je
površina toga tijela ako mu snaga zračenja iznosi 400 W?
106.
Koji od grafova prikazuje ovisnost brzine o vremenu za jednoliko ubrzano gibanje?
107.
Na tijelo djeluje ukupna sila koja se mijenja duţ puta kako je prikazano na grafu. Tijelo početno
miruje.
Koliko iznosi kinetička energija tijela nakon što je ono prešlo 3 m? Trenje se zanemaruje.
A.
0 J
B.
20 J
C.
25 J
D.
30 J

20
C.
(1.51 ± 0.02) V
D.
(1.51 ± 0.03) V
115.
Baterija u strujnome krugu prikazanome na crteţu ima elektromotorni napon
E
. Smatra se da su
ampermetar i voltmetar idealni.
Kako će se promijeniti iznosi na mjernim ureĎajima kada se zatvori prekidač P?
A.
Iznos na ampermetru će se povećati, a na voltmetru smanjiti.
B.
Povećat će se iznosi i na ampermetru i na voltmetru.
C.
Iznos na ampermetru će se smanjiti, a na voltmetru povećati.
D.
Smanjit će se iznosi i na ampermetru i na voltmetru.
116.
Na grafu je prikazana ovisnost jakosti struje
I
o naponu
U
za dva vodiča.
Koliko bi iznosio ukupni otpor serijskoga spoja tih dvaju vodiča?
A.
0.23 Ω
B.
4.3 Ω
C.
25 Ω
D.
35 Ω
117.
Dva točkasta naboja u zraku se meĎusobno odbijaju silom 2 μN. Naboji su smješteni na jednak
razmak u sredstvo relativne dielektrične konstante 8. Kolika je sila izmeĎu tih naboja u navedenome
sredstvu?
A.
0 N
B.
0.25 μN
C.
2 μN
D.
16 μN
118.
Konvergentna leća stvara sliku predmeta na zastoru udaljenome 12 cm od leće. Ţarišna daljina
leće je 6 cm. Kolika je udaljenost izmeĎu predmeta i slike toga predmeta?
A.
18 cm
21
B.
20 cm
C.
22 cm
D.
24 cm
119.
Točkasti izvor vala titra frekvencijom 50 Hz. Val se širi brzinom od 300 m/s. Kolika je razlika u
fazi izmeĎu točaka koje su 2 m i 8 m udaljene od izvora?
A.
0 rad
B.
π rad
C.
6 rad
D.
2π rad
120.
Vremenska ovisnost elongacije tijela koje harmonijski titra dana je izrazom
y
= 2 cm sin(π s
–1
t
).
Kako glasi izraz za brzinu toga tijela u ovisnosti o vremenu?
A.
v
= 2 cm/s sin(2π s
–1
t
)
B.
v
= 2π cm/s sin(π s
–1
t
)
C.
v
= 2 cm/s cos(2π s
–1
t
)
D.
v
= 2π cm/s cos(π s
–1
t
)
121.
Infracrveno zračenje valne duljine 2 μm nailazi na pregradu s dvjema pukotinama meĎusobnoga
razmaka 1 mm. Maksimumi interferencije detektiraju se na udaljenosti 1 m od pregrade. Koliki je
razmak izmeĎu susjednih maksimuma interferencije?
A.
1 mm
B.
2 mm
C.
3 mm
D.
4 mm
122.
Tijelo vezano na oprugu titra oko ravnoteţnoga poloţaja. Kako se naziva najveći pomak od
ravnoteţnoga poloţaja?
A.
period
B.
frekvencija
C.
elongacija
D.
amplituda
123.
Od 10 000 jezgri nekoga radioaktivnoga izotopa u prva se četiri dana raspadne 5000 jezgri. Koja
je od navedenih tvrdnji točna?
A.
U prva se dva dana raspalo 2 500 jezgri.
B.
U sljedeća će se četiri dana raspasti preostalih 5 000 jezgri.
C.
U prva se dva dana raspalo više jezgri nego u sljedeća dva dana.
D.
Svaki se dan raspadne jednaki broj jezgri.
124.
Kojoj vrsti zračenja pripadaju fotoni energije 2 eV?
A.
gama zračenju
B.
vidljivoj svjetlosti
C.
mikrovalnomu zračenju
D.
radiovalovima
125.
Na crteţu je shematski prikazan dio energijskoga spektra nekoga atoma.

23
130.
Balon mase 90 kg pada kroz zrak. Na balon djeluju sila otpora zraka od 300 N i sila uzgona od 60
N. Kolikom akceleracijom pada balon?
131.
Tijelo mase 3 kg guramo jednoliko duţ kosine koja je dugačka 4 m, a visoka 2 m. Trenje
zanemarujemo. Koliki se rad izvrši nad tijelom ako ga se gura od dna do vrha kosine?
132.
Obujam idealnoga plina pri temperaturi od 293 K je 1 m
3
. Pri stalnome tlaku temperatura
idealnoga plina naraste na 353 K. Odredite obujam plina pri toj temperaturi.
133.
Zavojnica induktiviteta 0.25 H i kondenzator serijski su spojeni na izvor izmjeničnoga napona
frekvencije 60 Hz. Izračunajte kapacitet kondenzatora ako je njegov kapacitivni otpor jednak
induktivnomu otporu zavojnice.
134.
Zraka svjetlosti upada iz zraka pod kutom od 60° prema okomici na mirnu površinu tekućine.
Izračunajte apsolutni indeks loma tekućine ako je kut izmeĎu odbijene i lomljene zrake 90°.
135.
Astronautkinja putuje raketom koja se giba jednoliko po pravcu brzinom
u odnosu na Zemlju.
Ona je u svojem sustavu izmjerila da njezino putovanje traje 2 godine. Koliko je vremena putovanje
trajalo za promatrača na Zemlji?
136.
Na tijelo mase 30 kg djeluje se silom
F
pod kutom od 30° prema horizontali.
Tijelo se giba jednoliko. Faktor trenja izmeĎu tijela i podloge je 0.1. Odredite iznos sile F.
137.
Grijačem snage 500 W tali se 2 kg leda temperature 0 °C. Sva energija koju proizvede grijač
potroši se na taljenje leda. Za koliko se vremena led rastali? Specifična toplina taljenja leda iznosi 330
000 J kg
–1
.
138.
Dva duga, ravna i meĎusobno paralelna vodiča nalaze se u homogenome magnetskome polju od
2·10
−6
T. Vodičima teku struje 10 A u istome smjeru.
Vodiči se nalaze u ravnini okomitoj na silnice magnetskoga polja i meĎusobno su udaljeni 0.2 m.
Kolika je ukupna sila na 1 m duljine vodiča kojim teče struja
I
1
?
139.
Duljina neopterećene elastične opruge je 0.15 m. Na oprugu ovjesimo uteg mase 0.1 kg i
zatitramo. Period harmonijskoga titranja utega na opruzi iznosi 0.5 s. Kolika će biti duljina opruge
opterećene tim utegom nakon što titranje prestane?
140.
Kugla temperature 200 °C i površine 2·10
–4
m
2
zrači kao crno tijelo. Koliko energije u vremenu
od 60 sekundi kugla izrači u okolinu uz pretpostavku da joj se temperatura pri zračenju ne mijenja?
24
RJEŠENJA I POSTUPCI RJEŠAVANJA
1
.
Za ubrzano gibanje je
; graf te funkcije je parabole
.
Za jednoliko gibanje je
; graf je dio pravca
.
Za jednoliko usporeno gibanje je
; graf je
dio parabole
.
Vrijeme se računa od , odnosno .
Odgovor: D
2.
t
= 8 s
Put je po brojčanoj vrijednosti jednak površini omeĎenoj krivuljom
v
(
t
) , ordinatama brzine i osi
t
.
Površinu je najlakše izračunati zbrajajući površine trapeza ABCD (
s
1
) i BGFC (
s
2
).
Odgovor: D
3
.
Odgovor: B
4.
= početna brzina
Odgovor: B
O
A
B
C
x
t
t
t
A
B

26
9.
Kod izohornog procesa tlak
p
raste linearno s temperaturom,
pa je moguć samo odgovor
pod A.
Odgovor: A
10.
T
2
= 4
T
1
V
2
= 2
V
1
p
= ?
27
15.
Pregorjela je ţaruljica
c
čime je prekinut glavni strujni krug.
Odgovor: C
16.
Odgovor: B
17.
Odgovor: A
18.
Pravilo desne ruke govori da palac desne ruke postavimo u smjer struje, pa će nam zakrivljeni prsti
pokazati smjer magnetskog polja. Magnetska polja u točki T imaju isti smjer pa se njihove vrijednosti
zbrajaju.
Odgovor: D
19.
Odgovor: B
20.
Odgovor: B

29
Odgovor:
27.
Odgovor:
28.
30
31.
31.1.
Odgovor:
31.2.
Odgovor:
32.
Gravitacijsku silu
rastavljamo na dvije vektorske komponente
u smjeru gibanja tijela i
okomitu na smjer gibanja tijela.
32.1.
Odgovor:
32.2.

32
36.
Iz grafa očitati akceleracije tijela i pripadajuća im vremena koja treba uvrstiti u formulu
,
odnosno
i izračunati
- razlike brzina. Podatke je najpraktičnije posloţiti u tablicu:
Očitano s grafa
a
= 3 m s
–2
a
= 0 m s
–2
a
= 1 m s
–2
a
= 0 m s
–2
Očitano s grafa
Izračunato
m s
–1
m s
–1
m s
–1
m s
–1
U trenutku
t
= 0 s tijelo miruje, tj.
= 0 m/s - točka (0, 0). Tijekom prve 2 s brzina se tijelu promijeni
s 0 na 6 m s
–1
- točka (2, 6). Sljedeće 2 s, dakle ukupno nakon 4 s nema promjene brzine i ona je 6
- točka (4, 6). Od 4. do 6. sekunde, brzina se promijeni za 2 m s
–1
i to s dotadašnjih 6 na 8 m s
–1
- točka (6, 8). U 7. sekundi nema promjene brzine i ona je 8 m s
–1
- točka (7, 8). Tim točkama
odgovara samo graf
Odgovor: A
37.
_________
Odgovor: D
38.
Ukupna količina gibanja prije sudara jednaka je ukupnoj količini gibanja poslije sudara:
Odgovor: A
39.
Tijela s manjom gustoćom od vode, na vodi plivaju dok tijela s većom gustoćom tonu. Tijela jednake
gostoće kao voda u vodi plutaju, tj. ostaju na onom poloţaju u vodi u koji ih stavimo pa vrijedi:
ρ
K
<
ρ
=
ρ
L
.
Odgovor: B
33
40.
Odgovor: B
41.
Čestice idealnog plina uopće nemaju potencijalnu energiju.
Odgovor: A
42.
T
1
= 0 °C = 273 K
_______
= ?
Za dva stanja iste količine plina vrijedi:
Odgovor: D
43.
Kada se kugle dotaknu, njihovi potencijali bit će jednaki:
Kako je
⇒
nC.
Odgovor: B
44.
= 12 V
I = 2 A
R
2
= 4 Ω
U
1
= ?
Drugo Kirchhoffovo pravilo: Zbroj svih napona u strujnoj petlji jednak je nuli.
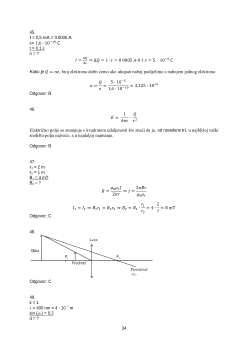
35
Odgovor: B
50.
Iz grafa očitamo maksimum krivulje na
y
(vertikalnoj) osi.
Odgovor: C
51.
v
A
= 100 m s
–1
λ
A
= 0.5 m
λ
B
= 0.8 m
v
B
= ?
Prolazom vala iz sredstva A u sredstvo B mijenjaju mu se brzina i valna duljina ali ne i frekvencija.
Odgovor: D
52.
Kad se oscilator nalazi u amplitudnim poloţajima, ukupna energija je pohranjena u opruzi pa sustav
ima samo potencijalnu energiju. U ravnoteţnom poloţaju, ukupnu energiju sustava čini samo kinetička
energija.
Odgovor: D
53.
Prelazeći iz stanja više energije u stanje niţe energije, atom emitira višak energije u obliku fotona
energije
Odgovor: A
54.
Odgovor: D
55.
Z
1
=7
Z
2
=2
Z
4
=1
A
2
=4
36
A
3
=17
A
4
=1
a,b
=?
Kod svake nuklearne reakcije zbroj masenih brojeva A mora biti jednak prije i poslije reakcije.
Isto je i s rednim brojevima Z
Odgovor: D
56.
Odgovor: A
57.
Odgovor: B
58.
Gibanje u vertikalnom smjeru (pad) ne ovisi o gibanju u horizontalnom smjeru. Pad s jednake visine u
oba slučaja vremenski traje jedako.
Odgovor: B
59.
Količina gibanja
Odgovor: A
60.

38
Odgovor:
66.
_________
Odgovor:
67.
(lonac je napravljen od aluminija)
_____________________
Odgovor:
39
68.
68.1.
Odgovor:
68.2.
Odgovor:
Kako je
q
< 0, sila će imati smjer vektora
69.
Odgovor:
70.

41
v
1
= 4 m s
–1
v
2
= 2 m s
–1
v=?
Ukupna količina gibanja prije sudara jednaka je ukupnoj količini gibanja poslije sudara:
Odgovor: D
74.
Tijela s manjom gustoćom od vode plivaju na vodi. Tijela s većom gustoćom od vode tonu u vodi.
Tijela s gustoćom jednakoj gustoći vode plutaju u vodi, tj. ostaju u vodi na mjestu gdje ih ostavimo.
Odnosno
ρ
K >
ρ
=
ρ
L
Odgovor: C
75.
Stupanj K jednak je °C samo su im ishodišta (poloţaj nule na skali) različita.
Odgovor: A
76.
Odgovor: C
77.
T
1
= 0 °C = 273 K
_______
= ?
Za dva stanja iste količine plina vrijedi:
Odgovor: D
78.
Kada se kugle dotaknu, njihovi potencijali bit će jednaki:
42
Kako je
⇒
nC.
Odgovor: C
79.
= 12 V
U
1
= 4 A
R
2
= 4 Ω
I = ?
Drugo Kirchhoffovo pravilo: Zbroj svih napona u strujnoj petlji jednak je nuli.
Odgovor: B
80.
t
= 0.1 s
______________
Odgovor: A
81.
Električno polje se smanjuje s kvadratom udaljenosti pa je u najbliţoj točki najveće, a u najdaljoj
najmanje. Električno polje i sila su proporcionalni pa isto vrijedi i za silu.
Odgovor: C
82.
r
1
= 2 m
B
1
= 2 mT = 0.002 T
B
2
= 4 mT = 0.004 T
μ
0
= 4π ·10
-7
r
2
= ?
i
44
87.
Kad se oscilator nalazi u amplitudnim poloţajima, ukupna energija je pohranjena u opruzi pa sustav
ima samo potencijalnu energiju. U ravnoteţnom poloţaju, ukupnu energiju sustava čini samo kinetička
energija.
Odgovor: D
88.
Kad atom prelazi iz stanja niţe energije u stanje više energije apsorbira energiju jednaku razlici
energija tih stanja.
Odgovor: B
89.
Odgovor: D
90.
Z
2
= 2
Z
3
= 8
Z
4
= 1
A
1
= 14
A
2
= 4
A
4
= 1
a,b
=?
Kod svake nuklearne reakcije zbroj masenih brojeva A mora biti jednak prije i poslije reakcije.
Isto je i s rednim brojevima Z
Odgovor: A
91.
Odgovor: B
92.
Odgovor: B
93.
H
= visina
45
D
= domet
= početna brzina
Kako je
Odgovor: A
94.
λ
= valna duljina
h
= Planckova konstanta
Količina gibanja
Odgovor: A
95.
Odgovor:
96.
ili bilo koja druga masa

47
101.
Odgovor:
102.
48
103.2.
Odgovor:
Kako je q < 0
⇒
sila će imati smjer samo vektora
.
104.
Odgovor:
105.
Odgovor:
106.
govori da je brzina linearno proporcionalna vremenu.
Odgovor: A
v
F

50
Kako je
što znači da je početna pretpostavka točna.
Odgovor: B
112.
k =
Boltzmanova konstanta
Odgovor: C
113.
m
= 0,5 kg
r
= 2260 kJ/kg
Q
= ?
Q
=
m
·
r
= 0,5 · 2260 = 1130
Kondenzacijom se oslobodi toplina jednaka toplini isparavanja.
Odgovor: A
114.
Najveće ostupanje je 1,53 – 1,51 = 0,02 V pa je
U
= (1,51 ± 0,02) V
Odgovor: C
115.
Neka su
I
1
i
U
1
vrijednosti prije uključivanja sklopke, a
I
2
i
U
2
nakon uključivanja. Tada je
51
Odgovor: A
116.
Odgovor: D
117.
F
1
= 2 µN
__________
F
2
= ?
Odgovor: B
118.
b
= 12 cm
f
= 6 cm
a
+
b
= ?
Odgovor:D
119.
v =
300 m/s
f
= 50 HZ
x
1
= 2 m
x
2
= 8 m
Odgovor: D
120.
Odgovor:D

53
127.
_________________________
Odgovor: A
128.
Nema doticaja štapa i elektroskopa pa nema prijelaza naboja, već se na elektroskopu naboj samo
prerasporedi, ali ukupan naboj ostaje isti, tj. nula.
Odgovor: C
129.
Odgovor: A
130.
m
= 90 kg
T
= 300 N
U
= 60 N
a
= ?
Odgovor:
131.
m
= 3 kg
h
= 2 m
W
= ?
(pretpostavka
)
Odgovor: 60 J
U
60 N
T
300 N
mg
h = 2 m
4 m
54
132.
V
A
= 1 m
3
T
A
= 293 K
T
B
= 353 K
V
A
= ?
Odgovor:
133.
L
= 0,25 H
f
= 60 Hz
C
= ?
Odgovor:
134.
α =60°
N
= ?
Odgovor:
n
= 1,73
135.
T
A
= 2 god
T
Z
= ?
p
V
A
B
L
C
= ?
f

56
Odgovor:21,3 cm
140.
T
= 200 °C = 473 K
S
= 2·10
–4
m
2
t
= 60 s
E
= ?
Odgovor: 34 J
l
l
x
Želiš da pročitaš svih 1 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































