Miroslava Unkaševi
ć
Dragana Vujovi
ć
Ivana Toši
ć
Zbirka zadataka iz
klimatologije i
primenjene meteorologije
Savezni hidrometeorološki zavod
Beograd, 2002.
Autori
:
dr Miroslava Unkaševi
ć
mr Dragana Vujovi
ć
mr Ivana Toši
ć
Zbirka zadataka iz klimatologije i
primenjene meteorologije
Recenzenti:
dr Jovan Mališi
ć
, red. prof.
dr Lazar Lazi
ć
, van. prof.
Izdava
č
:
Savezni hidrometeorološki zavod
Bir
č
aninova 6, Beograd
Za izdava
č
a
:
Mom
č
ilo Živkovi
ć
, dipl. meteorolog
Štampa
: AG Print, Beograd
Prelom teksta
: Dragana Vujovi
ć
i Ivana Toši
ć
Slike
: Dragana Vujovi
ć
i Ivana Toši
ć
Korice
: Dragana Vujovi
ć
i Vladimir Stojši
ć
CIP-Kata
логизација
у
публикацији
Народна
библиотека
Србије
,
Београд
55
1
.50 (075.8) (076)
55
1
.58 (075.8) (076)
УНКАШЕВИЋ
, M
ирослава
Zbirka zadataka iz klimatologije i
primenjene meteorologije /
М
iroslava
Unkaševi
ć
, Dragana Vujovi
ć
, Ivana Toši
ć
. -
Beograd: Savezni hidrometeorološki zavod,
2002 (Beograd: AG Print). –II, 238
str.: graf. prikazi; 24 cm
Tiraž 200. –Bibliografija: str. 233-234.
ISBN 86-809
11
-
1
2-7
1
.
Вујовић
,
Драгана
2.
Тошић
,
Ивана
а
)
Метеорологија
–
Задаци
б
)
Климатологија
–
Задаци
COBISS-ID 96
11
9820
Zbirka zadataka iz klimatologije i primenjene meteorologije
i
M. Unkaševi
ć
, D. Vujovi
ć
, I. Toši
ć
Sadržaj
strana
1. Zra
č
enje
1
.
1
Uvod
1
2. Klima i vodni resursi
2.
1
Crtanje hidrograma i sumarne linije oticaja
49
2.
1
.
1
Odre
đ
ivanje zapremine pale vode
49
2.
1
.2 Crtanje hidrograma
50
2.
1
.3 Izra
č
unavanje zapremine pale vode i koeficijenta oticaja
5
1
2.
1
.4 Konstrukcija sumarne linije oticaja
5
1
2.2 Ocena verovatno maksimalnih padavina, PMP,
pomo
ć
u Heršfildovog (statisti
č
kog) metoda
55
2.2.
1
Uzorak podataka
55
2.2.2 Predstavljanje retkih doga
đ
aja
55
2.2.3 Nezavisnost i slu
č
ajnost promenljive
M
K
56
2.2.4 Odnos izme
đ
u
M
K
i povratnog perioda
56
2.2.5 Aritmeti
č
ka sredina niza godišnjih maksimuma
56
2.2.6 Standardna devijacija niza godišnjih maksimuma; uticaj
mogu
ć
eg izuzetka
56
2.2.7 Koeficijent varijacije
57
2.2.8 Empirijska korekcija zbog grešaka u podacima
57
2.2.9 Procena PMP
57
3. Meteorologija u poljoprivredi
3.
1
Odre
đ
ivanje suma aktivnih temperatura
63
3.2 Odre
đ
ivanje dubine nulte izoterme
76
3.3 Prognoza mraza
80
3.4 Obrada podataka o visini padavina
87
4. Gradska klima
4.
1
Odre
đ
ivanje korelacija izme
đ
u klimatskih elemenata
99
4.2 Raspodele klimatskih elemenata
1
09
4.2.
1
Gumbelova raspodela
1
09
4.2.2 Dženkinsonova raspodela
11
2
4.3 Teorija pragova
1
34
5. Uticaj vremena i klime na
č
oveka
5.
1
Pokazatelji komfora
1
47
6. Prilog
1
6
1
Tabela I
1
63
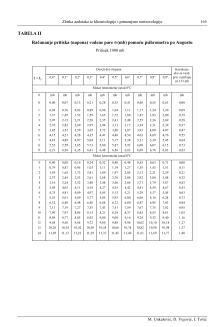
Tabela II
1
65
Tabela III
1
66
Tabela IV
1
73
Tabela V
2
1
5
Tabela VI
2
1
6
Tabela VII
2
1
8
2
Klima i energija
M. Unkaševi
ć
, D. Vujovi
ć
, I. Toši
ć
i diferenciranjem po
λ
x
T
x
c
d
d
2
2
−
=
λ
,
dobija se iradijansa crnog tela
( )
∫
∞
−
=
0
3
4
2
4
1
1
e
d
x
x
x
c
T
c
T
B
,
gde su radijacione konstante
2
1
6
2
1
Wm
1
0
74
,
3
h
2
−
⋅
=
π
=
c
c
,
mK
1
0
44
,
1
k
/
h
2
2
−
⋅
=
=
c
c
.
Plankova (Planck) konstanta iznosi
J
1
0
6255
,
6
h
34
−
⋅
=
,
dok je Bolcmanova (Boltzmann) konstanta
-
1
23
JK
1
0
38
,
1
k
−
⋅
=
,
a Štefan-Bolcmanova konstanta je
4
2
8
0
4
4
2
1
3
4
2
1
K
Wm
1
0
6696
,
5
1
5
d
1
e
−
−
−
∞
⋅
=
π
=
−
=
σ
∫
c
c
x
x
c
c
x
.
Dakle, Štefan-Bolcmanov zakon glasi
( )
4
T
T
B
σ
=
.
Z
ADATAK
1.1.2
Izvesti Vinov (Wien) zakon pomeranja tj. na
ć
i talasnu dužinu
λ
m
pri kojoj je
monohromatska iradijansa crnog tela maksimalna. Na osnovu ovog rezultata odrediti
λ
m
za
Sunce i Zemlju. Temperatura površine Sunca je
K
5800
s
=
T
, a temperatura površine Zemlje
je K
300
Z
=
T
.
Rešenje:
Da bi monohromatska iradijansa crnog tela bila maksimalna, prvi izvod iradijanse po
λ
mora da bude jednak nuli, a drugi izvod manji od nule, tj.
( )
0
d
d
=
λ
λ
T
B
,
(
1
)
( )
0
d
d
2
2
<
λ
λ
T
B
.
(2)
S obzirom na obrazac za
( )
T
B
λ
, prvi uslov zna
č
i
