Садржај:
1.
Увод …………………………………………………………………..…….
2
2.
Појам, значај и врсте средњих вредности ………………………..
3
2.1. Аритметичка средина …………………………………………………..
5
2.1.1. Аритметичка средина из негруписаних података ……….
5
2.1.2. Аритметичка средина из груписаних података ………..…
6
2.1.3. Особине аритметичке средине ……………………………….
10
2.2. Геометријска средина ………………………………………………….
11
2.3. Хармонијска средина ……………………………………….………….
13
2.3.1. Хармонијска средина за негруписане податке ……...……
14
2.3.2. Хармонијска средина за груписане податке …………...….
15
2.4. Медијана …………………………………………………….……………..
16
2.4.1. Медијана за негруписане податке ……………………………
17
2.4.2. Медијана неинтервалних серија дистрибуције
фреквенција ……………………………………………….………
18
2.4.3. Медијана интервалне серије дистрибуције
фреквенција ……………………………………………….………
20
2.5. Модус ………………………………………………………………….……
21
3.
Закључак ………………………………………………………………….. 25
4.
Литература ………………………………………………………………
25
1. УВОД
Кад споменемо реч „статистика“, прво се помисли на скуп нумеричких
података о стању неке појаве или на државну статистику. Као порекло речи
„статистика“наводи се латинска реч „
status
“, што значи стање, а статистика
описивање стања.
Треба узети у обзир да статистичке анализе датирају неколико векова
пре наше ере.
Прва позната пребројавања
спроведена су у Кини око 4.000
година пре нове ере и у Египту око 3.000 година пре нове ере, док су
први
организовани пописи
вршени у старом веку у Римској републици. У почетку,
основни задатак статистичког истраживања сводио се на прикупљање података
о бројном стању становника и војске, пописи земљишта и стоке. Обрада ових
података се изводила да би држава имала увид у своју војну и финансијску моћ.
У XVI веку установљени су у неким европским земљама и регистри рођених,
умрлих и венчаних, из којих се касније развила статистика природног кретања
становништва.
Зачеци статистике као науке
настали су у Немачкој и Енглеској у VXII
веку. Немачка школа статистике развила је
методе за дескрипцију појаве
.
Енглеска школа уводи у статистику
математичке методе
и
анализу података
чиме је отворен пут брзом развоју статистике. Коришћење теорије вероватноће
у статистици, које датира од XIX века, омогућило је развој теоријске статистике.
Такође, развој и коришћење теорије вероватноће омогућили су и развитак
нових статистичких теорија, као што је
статистичка теорија одлучивања
.
Данас
,
статистика је посебна научна дисциплина
која за реализацију
постављених циљева истраживања на организован начин прикупља, врши
одабир и груписање података, презентује и врши анализу података, те
интерпретира резултате спроведене анализе. Из изложеног изводимо
дефиницију да се
статистика као наука бави прикупљањем, обрадом и
анализирањем података о масовним појавама
.
У овом раду посветићу пажњу
појму средње вредности
која се у
литератури среће под називом
мера централне тенденције
.
2
спремачице. Рачунски, то је једноставан поступак јер су све плате у динарима,
па их можемо сабрати и поделити са четири. Међутим, шта такав просек значи
и чију плату представља? Из вредности таквих хетерогених јединица не може
се добити репрезентативна вредност у статистичком смислу. Сасвим други
случај је ако израчунамо просечну плату свих спремачица.
Исто тако, и приликом упоређивања средњих вредности два статистичка
скупа води се рачуна о хомогености тих скупова. Значи, при одређивању и
примени средњих вредности мора бити задовољен принцип хомогености
статистичког скупа.
Средња вредност датог обележја у статистичком скупу може се одредити
по разним мерилима: као вредност која се израчунава на основу свих
вредности посматраног обележја или изабрати између конкретних вредности
обележја према положају који заузима у серији.
Према томе да ли се
израчунавају или одређују према положају појединих вредности обележја,
средње вредности се могу поделити у две групе
:
потпуне средње вредности
– рачунају се употребом свих података
у статистичком низу; ту спадају аритметичка средина, хармонијска средина и
геометријска средина
положајне средње вредности
– одређују се положајем података у
низу, а најважније положајне средње вредности су модус и медијана
1
Свака од поменутих средњих вредности одређује се посебним
статистичко-математичким методама и има одређене карактеристике. Средње
вредности се не могу израчунати, односно одредити код свих серија. Оне се
израчунавају, односно одређују само код нумеричких распореда фреквенција, а
могу се израчунати из временских серија. За утврђивање карактеристика
распореда фреквенција оне представљају полазну основу.
Средња вредност једне серије не може бити мања од најмање вредности
обележја, нити већа од највеће вредности обележја. Средња вредност може
бити и нека вредност која уопште не постоји у серији – нпр. у једном предузећу
може бити просечна плата 557 динара, а да нико у том предузећу такву плату
нема. Средња вредност може имати и децималан број, иако се вредности
1
Квргић Г.:
Основи финансијске статистике
, Висока пословна школа струковних студија,
Чачак, 2008.
4
обележја изражавају у целим бројевима – нпр. просечан број чланова
домаћинства може бити 3,4.
2.1. АРИТМЕТИЧКА СРЕДИНА
Најширу употребу у статистичким истраживањима, као и у свакодневном
животу, стекла је аритметичка средина или како се популарно назива просек. У
практичном животу често се говори о просечној производњи, просечној заради,
просечној потрошњи млека, просечној тежини итд.. Аритметичку средину
добијамо кад збир свих вредности обележја поделимо њиховим бројевима
2
.
Аритметичка средина може се израчунати из груписаних и негруписаних
података
.
2.1.1. АРИТМЕТИЧКА СРЕДИНА ИЗ НЕГРУПИСАНИХ ПОДАТАКА
Кад су подаци негруписани, односно кад се сваки податак јавља само
једанпут (са фреквенцијим 1), аритметичка средина се израчунава тако што се
збир вредности обележја подели њиховим бројем. Ако се поједине вредности
обележја означе са
x
1
, x
2
, x
3
,..., x
n
, њихов број са
n
(који представља број
јединица посматрања), а аритметичка средина са x (иск са цртом чита се: иск
бар), израчунавање аритметичке средине из негруписаних података може се
изразити следећим обрасцем:
x =
x
1
+ x
2
+ x
3
+ ... + x
n
n
или ако збир означимо са ∑ (сигма)
x =
∑x
n
2
Квргић Г.:
Основи финансијске статистике
, Висока пословна школа струковних студија,
Чачак, 2008.
5
има већу фреквенцију, утолико јој је и значај већи, јер јаче утиче на величину
аритметичке средине.
Пондерисањем вредности обележја
обухватају се све
вредности датог обележја, јер множење појединачних вредности њиховом
фреквенцијом представља узимање те вредности толико пута колико се јавља.
Код аритметичке средине за негруписане податке узимају се све вредности
обележја, али пондерисања нема, зато што се свака вредност једном јавља и
према томе све вредности су подједнако значајне или важне.
За израчунавање пондерисане аритметичке средине узећемо као пример
податак о броју радника омладинаца иноватора (запослених у највећим
индустријским предузећима Србије) и о броју њихових проналазака којим су
допринели савременој и економичној производњи. Подаци груписани у виду
серије расподела фреквенција приказани су у табели 1. На основу ових
података и датог обрасца за израчунавање пондерисане аритметичке средине,
поступак израчунавања може се лакше и прегледније обавити помоћу радне
табеле, као што је табела 2.
Број проналазака
Број радника
3
2
5
8
8
5
10
3
12
2
Укупно
20
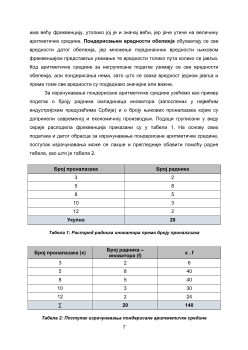
Табела 1: Распоред радника иноватора према броју проналазака
Број проналазака (x)
Број радника –
иноватора (f)
x . f
3
2
6
5
8
40
8
5
40
10
3
30
12
2
24
∑
20
140
Табела 2: Поступак израчунавања пондерисане аритметичке средине
7
