polja. Atomi su sastavni deo svake materije. Svojstvo atoma neophodno za magnetnu rezonancu
je nuklearni spin odnosno spinski moment impulsa. Svaki element koji se nalazi u prirodi, osim
cezijuma i argona ima najmanje jedan izotop sa nuklearnim spinom, što znači da se skoro svaki
element može proučavati pomoću MR. Osnovni koncepti apsorpcije energije, hemijskog pomaka
i opuštanja zajednički su svim takvim jezgrima, dok su ostali specifični detalji posebni za svako
jezgro. [2]

Atomska struktura pruža osnovu za opisivanje mnogih svojstava atoma. Unutar atoma

nazlaze se tri sastavna dela u različitim količinama: protoni, koji imaju pozitivno naelektrisanje;
elektroni,  koji  imaju  negativno  naelektrisanje;  i  neutroni,  koji  su  elektroneutralni.  Protoni  i
neutroni čine jezgro atoma, dok se elektroni nalaze u elektronskom omotaču koji okružuje samo
jezgro.  Tri  karakteristične  osobine  atoma  su  od  fundamentalnog  značaja.  Atomski  broj  je  broj
protona  u  jezgru.  To  je  primarni  indeks  koji  se  koristi  za  identifikaciju  elemenata.  Svi  izotopi
jednog  elementa  imaju  isti  atomski  broj.  Atomska  masa  je  ukupan  broj  protona  i  neutrona.
Protoni  i  neutroni  imaju  skoro  jednaku  masu  i  1800  puta  su  teži  od  elektrona,  tako  da  jezgro
sadrži najveći deo atomske mase. Izotopi su atomi istog elementra, koji imaju isti atomski broj,
ali  različitu  atomsku  masu.  Za  elemente  sa  više  izotopa,  relativne  količine  svakog  izotopa
odnosno priroda brojnost je veoma važna pri razmatranju sposobnosti ispitivanja jezgra pomoću
MR tehnika. Na primer, vodonik ima tri izotopa koji se pojavljuju u prirodi:

ili protijum,

ili deuterijum i

ili tricijum. Sva tri izotopa imaju jedan proton u jezgru, ali imaju nulu, jedan

ili dva neutrona. Izotop protijuma nalazi se u 99,9% svih atoma vodonika, što ga čini prirodnim
izborom za MR istraživanja vodonika, poput  spektroskopije  ili snimanja. Izotop deuterijuma  je
približno 0,1% ukupnog vodonika, dok je tricijum znatno manji od 0,1%. Treće svojstvo koje se
koristi  za  opisivanje  atoma  je  nuklearni  spin  odnosno  sopstveni  ugaoni  moment  nuklearnog
spina.  Potpuni  opis  nuklearnog  spina  i  njegovih  svojstava  zahteva  upotrebu  kvantne  mehanike.
Za većinu svrha u kliničkoj spektroskopiji, nekoliko ključnih karakteristika kvantne mehanike je
dovoljno  za  opisivanje  ponašanja  jezgra.  Osim  toga,  za  biološke  sisteme,  takozvana
aproksimacija "visoke temperature" potvrđuje upotrebu klasične mehanike u većini situacija. [2]

Nuklearni spin je važan jer je to uslov za MR. Važna karakteristika nuklearnog spina je

da je kvantovan odnosno može imati samo određene diskretne vrednosti. Ove vrednosti zavise od
specifične prirode jezgra.

Pronađene su tri klase vrednosti nuklearnog spina:

Nuklearna magnetno-rezonantna spektroskopija kroz primer u kliničkoj praksi

Nulti ili nikakav spin. Nulti spin se nalazi za jezgra sa parnom atomskom težinom i
atomskim brojem odnosno parnim brojem protona i neutrona. Takva jezgra se još
nazivaju parno-parna jezgra. Takva jegra, bez spina, ne mogu se ispitivati MR tehnikama.

Ceo broj odnosno celobrojne vrednosti spina. Celobrojne vrednosti spina (1,2,3,...)
nađene su za jezgra sa parnom atomskom težinom a neparnim atomskim brojem tj.
neparan broj protona i neutrona.

Poluceli brojevi. Poluceli spin (1/2, 3/2, 5/2,...) se nalazi za jezgra sa neparnom
atomskom težinom odnosno za paran broj protona i neparan broj neutrona ili obrnuto. Za
kliničku spektroskopiju ovo je najčešća klasa spinova (

, ?

). Neutroni,

protoni i elektroni takođe imaju spin u vrednosti od 1/2.

Važna posledica nuklearnog spina je to što sa njim povezujemo magnetno polje.

Korisna analogija za jezgro sa spinom je magnet sa šipkom. Šipkasti magnet ima severni i južni
pol, tačnije može se definisati veličina i orijentacija prema magnetnom polju. Jezgro sa spinom
može da se posmatra kao vektor ili magnetni dipol koji ima određenu veličinu i osu rotacije sa
određenom orijetacijom. Manipulacija orijentacijom spina pomoću radiofrekventnog (RF)
impulsa je osnova za merenja tehnikom nuklearne magnetne rezonance. [2]

Moment impulsa jezgra

Orbitalni moment impulsa

Kod kvantnomehaničkih vektora kao što je moment impulsa nukleona istovremeno se može
odrediti modul i projekcija vektora na jednu od osa (najčešće je to z osa). Modul vektora
momenta impulsa može uzimati sledeće vrednosti:

|?⃗| = ћ√?(? + 1)

l-orbitalni kvantni broj, l=0,1,2,3,...

Vrednosti projekcije vektora kvantovane magnetskim kvantnim brojem m:

= ћ?

-magnetski kvantni broj, uzima sve celobrojne vrednosti od -l do +l

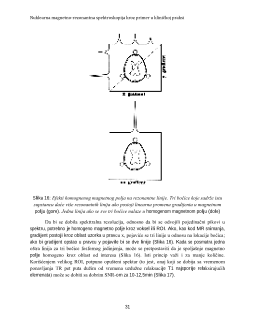
Orbitalni moment impulsa jezgra može u odnosu na neku posmatranu osu imati diskretan broj od
(2l+1) orijentacija od kojih se nijedna ne poklapa sa odabranim pravcem, već zaklapaju izvestan
ugao:

Nuklearna magnetno-rezonantna spektroskopija kroz primer u kliničkoj praksi

Slučaj kada nuklearne sile nisu centralnog tipa, znatno jače je izražena interakcija između
sopstvenog i orbitalnog momenta impulsa jednog nukleona. Tada se za svaki pojedinačni
nukleon, orbitalni i sopstveni moment impulsa sprežu u zajednički vektor. Ovakvo
sprezanje se još naziva i j-j sprega:

?⃗ = ?⃗ + ?⃗

Ukupan moment impulsa jezgra se u ovom slučaju dobija sabiranjem ukupnih momenata
impulsa pojedinačnih vektora:

?⃗ = ∑ ?

⃗⃗⃗

?=1

Ukupan moment impulsa celog jezgra poseduje sva svojstva kvantnomehaničkih vektora.

Vrednosti su mu kvantovane kao

√?(? + 1)

, dok su projekcije na z osu određene magnetnim

kvantnim brojem

, koji može uzimati sve brojne vrednosti u opsegu od -I do +I. Odatle sledi

da moment impulsa celog jezgra poseduje 2I+1 orijentacija odnosno energetskih podstanja koja
su ekvidistantna. Čak ni u jakim magnetnim poljima ne dolazi do razlaganja ukupnog magnetnog
momenta impulsa  jezgra I na 2j+1 komponentu, što  znali da se I ponaša kao sopstveni  moment
impulsa  jezgra  kao  celine.  Raznim  merenjima  primećeno  je  da  nukleoni  unutar  jezgra  mogu
imati  suprotno  orijentisane  spinove  pa  se  neki  od  njih  međusobno  mogu  poništiti.  Sva  parno-
parna  jezgra  (paran  broj  i  protona  i  neutrona)  bez  ijednog  izuzetka  u  svom  osnovnom
energetskom stanju poseduju  moment impulsa  jednak  nuli. Nulti  moment impulsa parno-parnih
jezgara  može  se  objasniti  činjenicom  da  unutar  jezgra  dolazi  do  sparivanja  nukleona  suprotno
orijentisanih vektora momenta impulsa.

Utvrđeno je i da jezgra sa neparnim brojem nukleona (paran broj protona, a neparan broj

neutrona  ili  obrnuto)  poseduju  polucele  vrednosti  spina  u  svom  osnovnom  energetskom  stanju.
Zaključuje  se  da  je  spin  neparnog  jezgra  jednak  momentu  impulsa  poslednjeg,  nesparenog
nukleona, jer svi spareni nukleoni ne doprinose ukupnom momentu impulsa jezgra.
Neparno-neparna  jezgra  odnosno  ona,  koja  imaju  parni  maseni  broj,  a  neparan  broj  protona  i
neparan  broj  neutrona  poseduju  celobrojne  vrednosti  spina  izražene  u    jedinicama,  dobijena
sabiranjem dva polucela broja. Ovo je moguće jedino ukoliko ne dolazi do sparivanja protona i
neutrona.  Odakle  sledi  zaključak  da  do  sparivanja  čestica,  prilikom  kog  dolazi  do  poništavanja
momenata impulsa, dolazi samo između istovetnih čestica tj. protona sa protonima i neutrona sa
neutronima. [1]