
Statistika
SADRŽAJ
Uvod
1. Deskriptivna statistička analiza
1.1. Mere centralne tendencije – srednje vrednosti
1.1.1. Aritmetička sredina
1.1.2. Geometrijska sredina
1.1.3. Harmonijska sredina
1.1.4. Modus
1.1.5. Medijana
2. Mere varijabiliteta, raspršenosti ili disperzije
2.1. Apsolutne mere varijacije
2.2. Relativne mere varijacije
3. Mere oblika rasporeda
3.1. Merenje asimetrije
3.2. Merenje spljištenosti
Zaključak
Literatura
Uvod
Promene i pojave u okruženju čoveka utiču na njegovo ponašanje zbog čega on oseća potrebu da te
promene i pojave prati, beleži, razmatra i objašnjava. Sa razvojem ljudskog društva menjao se i
način posmatranja i prikazivanja tih pojava, pa su se razvili metodi za njihovu deskripciju. Statis-
tika je naučni metod koji se primenjuje sa svrhom opisivanja, procene i analize karakteristika
grupa, bez identifikacije pojedinaca ili organizacija koje sačinjavaju takve grupe. Ona obuhvata
postupke i procedure prikupljanja, kompilacije, obrade i analize podataka o svim grupama i razvoj
sličnih metoda merenja, modela i statističkih klasifikacija u okviru uzorkovanja. Prema nekim au-
torima statistika je grana matematike koja preispituje načine procesuiranja i analize podataka. Ona
obezbeđuje uputstva za prikupljanje i oblikovanje podataka u formu koja je pogodna za donošenje
poslovnih odluka. Statistika se definiše i kao numerička mera koja opisuje karakteristike uzorka.
Jedna od definicija statistike naglašava da je statistika nauka koja se bavi prikupljanjem, klasi-
fikacijom i interpretacijom kvantitativnih podataka uz primenu teorije verovatnoće za analizu i
procenu parametara populacije. Savremena statistika obezbeđuje kvantitativne metode i tehnike za
potrebe empirijskih istraživanja. Ona sadrži metodologiju za merenje neizvesnosti i ispitivanje
posledica uticaja te neizvesnosti na planiranje i tumačenje rezultata eksperimentisanja i posma-
tranja. Predmet izučavanja statistike su masovne pojave čija je osnovna karakteristika varijabil-
nost. Varijabla predstavlja promenljive karakteristike atributa koji se razlikuju od osobe do osobe
ili od pojave do pojave, dok su podaci vrednosti posmatranih promenljivih. Upravo varijabilnost
pojave koja se ispoljava preko odstupanja vrednosti karakteristika izuzetnih slučajeva pojave od
opštih karakteristika te pojave koje odražavaju pravilnost njenog manifestovanja predstavlja ono
čime se statistika bavi. Statistika se može podeliti u dve celine: deskriptivna statistika čiji je za-
datak sumiranje podataka u lako razumljivu celinu i statističko zaključivanje koje podrazumeva
izvođenje zaključka o skupu na osnovu uzorka podataka
U statističkoj teoriji i praksi za opisivanje merenih pojava koriste se:
Mere centralne tendencije
Mere varijabilnosti i
Mere oblika rasporeda.
Mere centralne tendencije ukazuju na tendencije grupisanja rezultata merenja oko neke centralne
vrednosti. Mere varijacije pokazuju koliko odstupaju vrednosti obeležja od centralne vrednosti.
Mere oblika rasporeda pokazuju raspored vrednosti obeležja od najniže do najveće vrednost, o
čemu će više reči biti u nastavku.
Mere centralne tendencije ili srednjih vrednosti koriste se u svim oblastima statističke analize. U
zavisnosti od načina obračuna srednje vrednosti delimo na :
Izračunate srednje vrednosti kao što su:
-
aritmetička sredina ( ),
-
geometrijska sredina (G) i
-
harmonijska sredina (H).
Pozicione srednje vrednosti kao što su:
-
medijana (Me) i
-
modus (Mo).
Srednje vrednosti imaju nekoliko karakteristika. Jedna od karakteristika srednjih vrednosti je
neophodnost zavisnosti srednje vrednosti od svih vrednosti obeležja
x
u ukupnom statističkom
skupu. Takođe, srednja vrednost mora biti manja od najveće, a veća od najmanje vrednosti
obeležja. Kao posebna karakteristika srednjih vrednosti je da je srednja vrednost jednaka vrednosti
posmatranog obeležja u slučaju kada su međusobno jednake sve vrednosti obeležja koje se
posmatra u okviru jednog skupa.
Koja će se srednja vrednost upotrebiti zavisi od:
a) posmatrane pojave,
b) načina grupisanja u rasporedu frekvencija,
c) svojstva samih srednjih vrednosti.
Zajednicka svojstva srednjih vrednosti su:
Utvđuje se objektivnim matematičkim postupkom,
Njena vrednost se mora nalaziti između maksimalne i minimalne vrednosti (Xmin < sred-
nja vrednost < Xmax),
Ukoliko su te vrednosti obeležja međusobno jednake i srednja vrednost mora biti jednaka
toj vrednosti obeležja.
1.1.1. Aritmetička sredina
Aritmetička sredina predstavlja meru srednjih vrednosti sa kojom se najčešće susrećemo u
statističkim izveštajima. U odnosu na pozicione srednje vrednosti aritmetička sredina predstavlja
pouzdaniju meru srednjih vrednosti. Da bi se izračunala aritmetička sredina moraju biti ispunjena
dva uslova:25
Rezultati izvršenih merenja moraju biti dati u vidu intervalne ili racio skale;
Neophodno je da postoji pretpostavka o normalnom rasporedu rezultata izvršenih merenja
u skupu (uzorku).
Neke od najvažnijih karakteristika aritmetičke sredine date su u nastavku:26
Zbir odstupanja pojedinačnih vrednosti obeležja od vrednosti aritmetičke sredine iznosi
nula. Aritmetička sredina predstavlja meru srednjih vrednosti ukoliko je zbir svih
odstupanja pojedinačnih vrednosti obeležja sa pozitivnim znakom jednak zbiru svih
odstupanja pojedinačnih vrednosti obeležja sa negativnim znakom. Ova karakteristika
aritmetičke sredine može se dokazati primenom formule:
∑(
x
i
− x
) = 0
za negrupisane podatke
∑
f
(
x
i
− x
) = 0
za grupisane podatke
Zbir kvadratnog odstupanja pojedinačnih vrednosti obeležja od vrednosti aritmetičke
sredine je uvek minimalna vrednost, odnosno, manja vrednost od zbira kvadrata odstupanja
vrednosti obeležja od bilo koje druge vrednosti obeležja umesto od aritmetičke sredine.
S obzirom na to da se aritmetička sredina zasniva na svim vrednostima posmatranog
obeležja, promenom bilo koje vrednosti obeležja utiče se na promenu vrednosti aritmetičke
sredine.
U slučaju kada se u posmatranom uzorku nalaze ekstremne vrednosti koje značajno
odstupaju od ostalih vrednosti obeležja one značajno utiču na vrednost aritmetičke sredine.
U tom slučaju aritmetička sredina može prestati da bude reprezentativna mera centralne
tendencije.
Na osnovu analize aritmetičke sredine mogu se izdvojiti njene prednosti, ali i nedostaci.27
Prednosti primene aritmetičke sredine su sledeće:
Postupak obračuna aritmetičke sredine je jednostavan i jedinstven zbog toga što bilo koji
skup podataka može imati samo jednu vrednost aritmetičke sredine.
Aritmetička sredina se računa na osnovu svih vrednosti obeležja što je prednost jer nijedna
vrednost obeležja nije izostavljena.
Veličina uzorka nema uticaja na vrednost aritmetičke sredine. Ovo podrazumeva da u
slučaju kada imamo više uzoraka izvučenih iz jedne populacije podataka varijacije u
veličini aritmetičkih sredina različitih uzoraka biće manje.
Još jedna prednost aritmetičke sredine ogleda se u tome što se može izraziti primenom
algebarskog postupka.
Aritmetička sredina se koristi i kod međusobnog upoređivanja nekoliko serija podataka.
Nedostaci primene aritmetičke sredine su sledeći:
Kao najveći nedostatak aritmetičke sredine ističe se to što ona ne može da se izračuna u
nekim slučajevima. U slučaju kada je distribucija frekvencija data sa otvorenim intervalima
na početku ili na kraju, ili nejednakim klasama, aritmetička sredina neće biti precizno
izračunata.
Ukoliko skup statističkih podataka sadrži ekstremne vrednosti aritmetička sredina prestaje
da bude adekvatna mera centralne tendencije tog skupa podataka.
U slučaju kada je potrebno izračunati aritmetičku sredinu veoma velikog skupa podataka
njen obračun se usložnjava jer je neophodno obuhvatiti svaku vrednost obeležja
pojedinačno. Ovaj problem može biti rešen primenom metoda grupisanja podataka u manje
uzorke na osnovu kojih će se aproksimativno odrediti aritmetička sredina populacije.
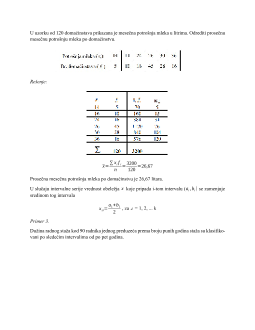
a) Za negrupisanu seriju podataka
Svaki podatak se javlja samo jednom aritmetička sredina se izračunava tako sto se zbir svih vred-
nosti obeležja podeli njihovim brojem. Aritmeticka sredina skupa, koju označavamo sa
x
, dobija se
kao:
x
=
x
1
+
x
2
+
…
x
n
N
=
1
N
∑
i
=
1
N
x
i
ili
x
=
∑
x
i
N
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































