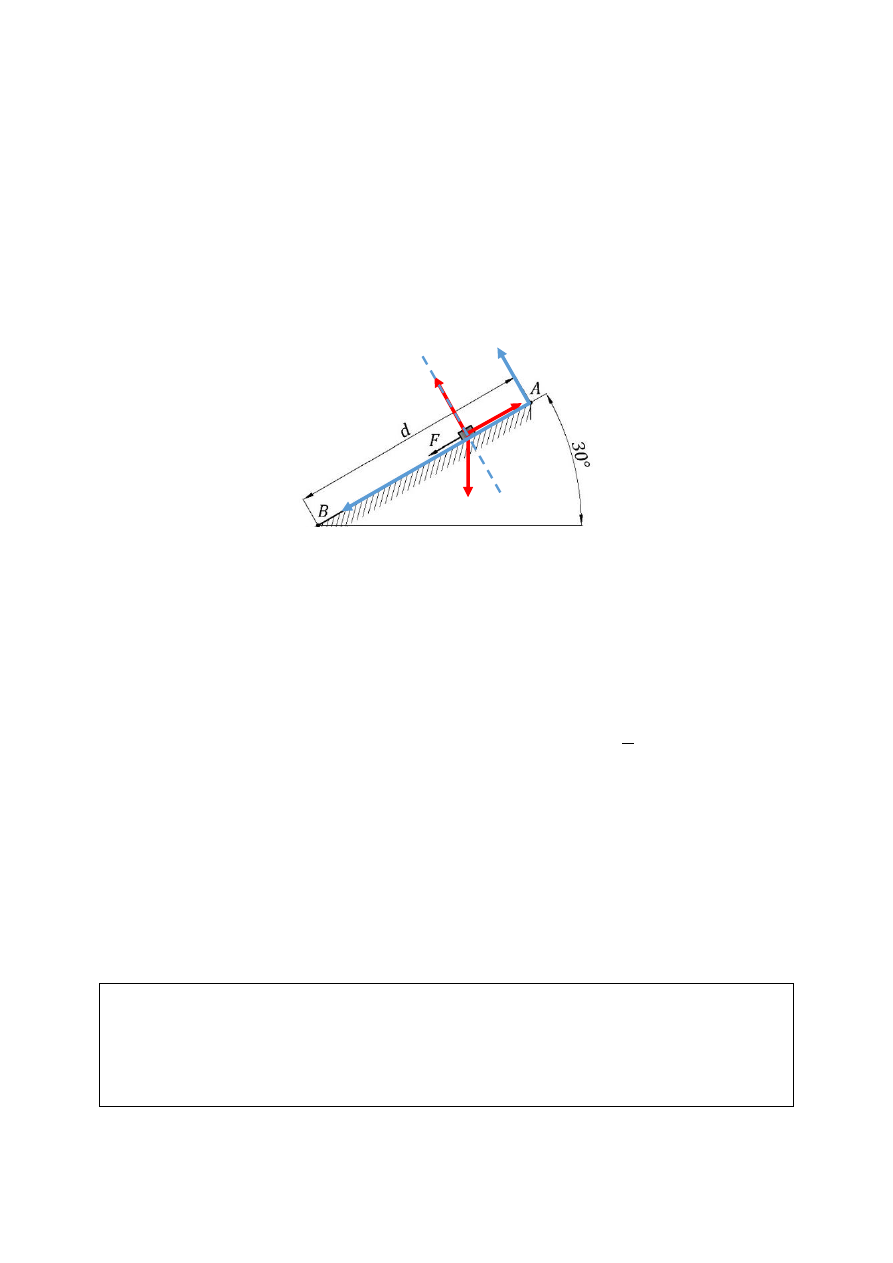
ЗАКОН О ПРОМЈЕНИ (ПРИРАШТАЈУ) КИНЕТИЧКЕ ЕНЕРГИЈЕ ТАЧКЕ
ЗАДАТАК БР. 1
Пакет масе
𝑚
започиње кретање низ стрму раван из положаја A без почетне
брзине. Све вријеме током кретања на пакет дјелује сила константног
интензитета
𝐹 = 2𝑚𝑔 [N]
у правцу стрме равни. Коефицијент динамичког
трења између пакета и подлоге је 0,58. Користећи се законом о промјени
кинетичке енергије тачке, одредити брзину пакета у положају B који се у
односу на положај A налази на растојању
𝑑 = 10 m
.
Интересује нас рад свих сила које дјелују на тачку на помјерању из положаја
А у положај В. Помјерање материјалне тачке врши се само у правцу осе
𝑥
.
𝑨
𝐴𝐵
𝑭
⃗⃗
= ∫ 𝐹 ∙ 𝑑𝑥
𝑥
𝐵
𝑥
𝐴
= ∫ 𝐹 ∙ 𝑑𝑥
10
0
= ∫ 2𝑚𝑔𝑑𝑥
10
0
cos 0 = ∫ 2𝑚𝑔𝑑𝑥
10
0
= 20𝑚𝑔
𝑨
𝐴𝐵
𝒎𝒈
⃗⃗
= ∫ 𝑚𝑔 ∙ 𝑑𝑥
𝑥
𝐵
𝑥
𝐴
= ∫ 𝑚𝑔 ∙ 𝑑𝑥
10
0
= ∫ 𝑚𝑔𝑑𝑥
10
0
cos 60° = ∫
1
2
𝑚𝑔𝑑𝑥
10
0
= 5𝑚𝑔
𝑨
𝐴𝐵
𝑵
⃗⃗
= ∫ 𝑁
⃗⃗ ∙ 𝑑𝑥
𝑥
𝐵
𝑥
𝐴
= ∫ 𝑁
⃗⃗ ∙ 𝑑𝑥
10
0
= ∫ 𝑁𝑑𝑥
10
0
cos 90° = 0
𝑨
𝐴𝐵
𝑭
⃗⃗
𝒕𝒓
= ∫ 𝐹
𝑡𝑟
∙ 𝑑𝑥
𝑥
𝐵
𝑥
𝐴
= ∫ 𝐹
𝑡𝑟
∙ 𝑑𝑥
10
0
= ∫ 0,5𝑚𝑔𝑑𝑥
10
0
cos 180° = −5𝑚𝑔
𝑚𝑎 = 𝐹 ⟹ {
𝑚𝑎
𝑥
= 𝐹 − 𝐹
𝑡𝑟
+ 𝑚𝑔 sin 30°
𝑚𝑎
𝑦
= 𝑁 − 𝑚𝑔 cos 30°
Кретање је
само
у правцу осе
𝑥
, што значи да је убрзање тачке у правцу осе
𝑦
једнако нули:
𝑚𝑔
𝑁
𝐹
𝑡𝑟
𝑥
𝑦
30
0 = 𝑁 − 𝑚𝑔 cos 30° ⟹ 𝑵 = 𝑚𝑔 cos 30° = 𝑚𝑔
√3
2
𝐹
𝑡𝑟
= 𝜇𝑁 = 0,58 ∙ 𝑚𝑔
√3
2
= 0,5𝑚𝑔
Укупан рад свих сила на помјерању тачке из положаја А у положај В је:
𝐴
𝐴𝐵
= 20𝑚𝑔 + 5𝑚𝑔 + 0 − 5𝑚𝑔 = 20𝑚𝑔
𝐸
𝑘𝐵
− 𝐸
𝑘𝐴
= 𝐴
𝐴𝐵
𝑚𝑣
𝐵
2
2
−
𝑚𝑣
𝐴
2
2
= 𝐴
𝐴𝐵
𝑚𝑣
𝐵
2
2
= 20𝑚𝑔
𝑣
𝐵
2
= 40𝑔
𝒗
𝑩
= 𝟐𝟎
𝐦
𝐬
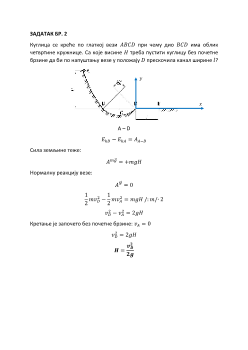
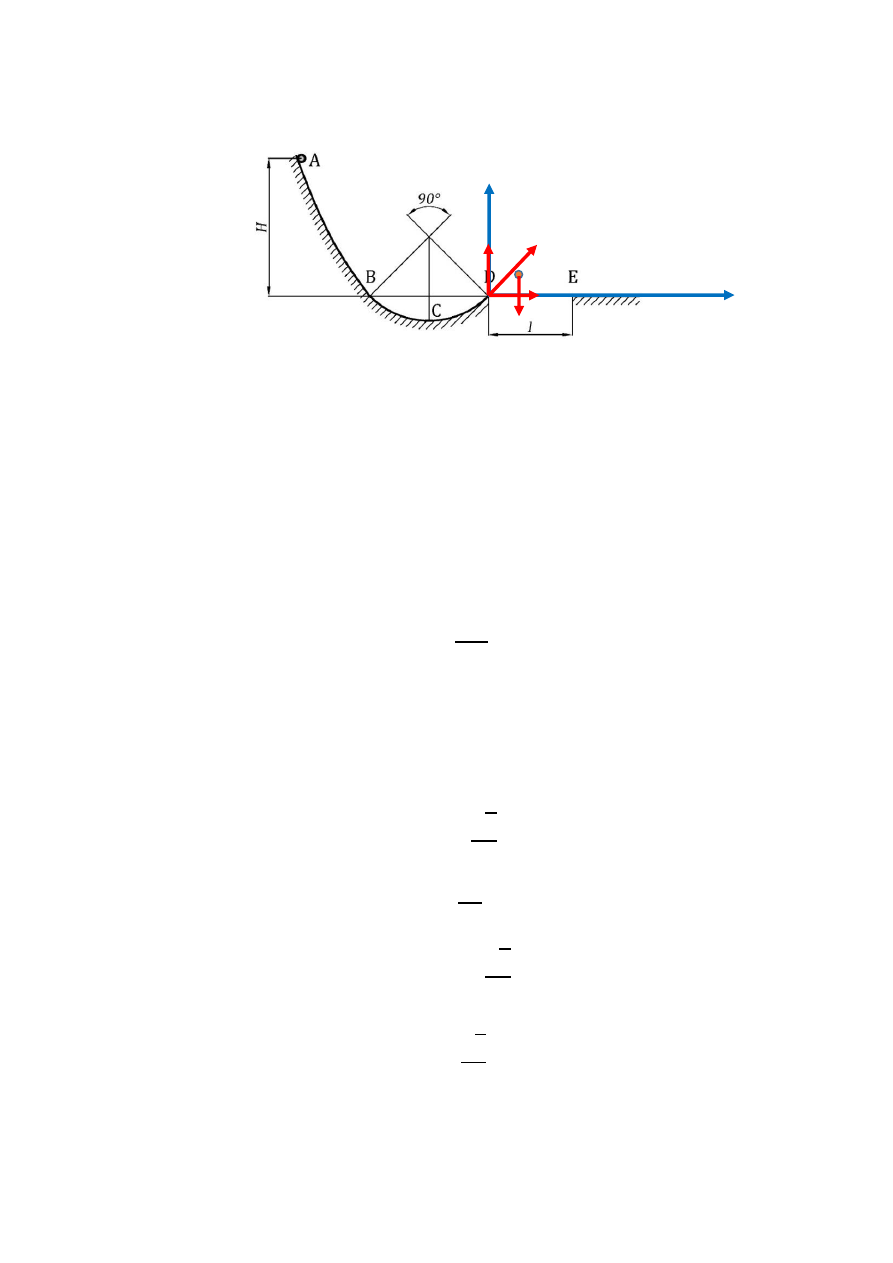
D – E
𝑚𝑎 = 𝐹 ⇒ {
𝑚𝑎
𝑥
= 0
𝑚𝑎
𝑦
= −𝑚𝑔
𝑎
𝑥
= 0
𝑎
𝑦
= −𝑔
𝑎
𝑥
= 0
𝑎
𝑥
=
𝑑𝑣
𝑥
𝑑𝑡
∫
𝑑𝑣
𝑥
𝑣
𝑥
𝑣
𝑥0
=𝑣
𝐷𝑥
=𝑣
𝐷
cos 45°
= 0 ∫ 𝑑𝑡
𝑡
0
𝑣
𝑥
− 𝑣
𝐷
cos 45° = 0
𝑣
𝑥
= 𝑣
𝐷
√2
2
𝑣
𝑥
=
𝑑𝑥
𝑑𝑡
∫
𝑑𝑥
𝑥
𝑥
0
=𝑥
𝐷
=0
= 𝑣
𝐷
√2
2
∫ 𝑑𝑡
𝑡
0
𝑥 = 𝑣
𝐷
√2
2
𝑡
Претходна релација важи за било који положај на дијелу D – E, па самим
тим важи и за Е:
𝑦
𝑥
𝑚𝑔
𝑣
𝐷
45°
45°
