
Betonske konstrukcije, fundiranje, tehnologija – beton
Univerzitet u Nišu
Gra
đ
evinsko-arhitektonski fakultet
DIPLOMSKI RAD
TEME:
BETONSKE KONSTRUKCIJE
FUNDIRANJE
TEHNOLOGIJA BETON
Student
Mentori
Marko Naki
ć
RG 6813/09
dr Predrag Blagojevi
ć
dr Zoran Boni
ć
dr Zoran Grdi
ć
SADRŽAJ
1. UVOD ........................................................................................................................................... 1
2. BETONSKE KONSTRUKCIJE .................................................................................................... 2
2.1 Prora
č
un sekundarnog nosa
č
a T45 ............................................................................................ 6
2.2 Prora
č
un glavnog nosa
č
a T120 ............................................................................................... 25
2.3 Prora
č
un stubova .................................................................................................................... 44
2.4 Grafi
č
ki prilozi za betonske konstrukcije ................................................................................ 59
3. FUNDIRANJE .............................................................................................................................. 70
3.1 Prora
č
un montažne
č
ašice ....................................................................................................... 70
3.2 Grafi
č
ki prilozi za fundiranje .................................................................................................. 75
4. TEHNOLOGIJA BETONA ......................................................................................................... 77
4.1 Prora
č
un ................................................................................................................................. 77
5. ZAKLJU
Č
AK ............................................................................................................................. 84
6. LITERATURA ............................................................................................................................ 85
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
2
2. BETONSKE KONSTRUKCIJE
Na osnovu zadate dispozicije objekta, uraditi klasi
č
no armiranje i prethodno naprezanje
sekundarnog nosa
č
a T45 i glavnog nosa
č
a T120 a zatim uporediti rezultate. Prednaprezanje izvršiti
tako da naponi u svim presecima i u svim merodavnim fazama duž nosa
č
a budu u granicama
dozvoljenih. Prilikom prora
č
una u I iteraciji koristiti pretpostavljene gubitke, a zatim uraditi prora
č
un
sa ta
č
nim gubicima i dati odgovaraju
ć
e komentare. Stubove prora
č
unati prema BAB ’87 i armirati ih
klasi
č
no. Grafi
č
ki prikazati usvojena rešenja.
U nastavku su dati crteži na osnovu kojih je vršen prora
č
un.

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
6
2.1 PRORA
Č
UN SEKUNDARNOG NOSA
Č
A T45
Klasi
č
no armiranje
Zbog malog nagiba od 6% rožnja
č
a je ra
đ
ena kao da je horizontalna, tako da je savijanje oko slabije
ose zanemareno.
Analiza optere
ć
enja
Stalno optere
ć
enje
−
sopstvena težina:
∗
0,0925 ∗ 25 2,3125 / ’
−
težina krovnog pokriva
č
a:
∗
0,3 ∗ 3 0,9 / ’
−
sneg i vetar:
∗
1,0 ∗ 3 3,0 / ’
−
instalacije:
∗
0,2 ∗ 3 0,6 / ’
∑
6,8125 / ′
Povremeno optere
ć
enje
∑
0 / ′
Zadati sistem i stati
č
ki sistem
Stati
č
ki sistem i shema optere
ć
enja

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
8
O
č
itano iz tabele:
3,454 → q̅ 8,851 % s
0,947 t 0,366 u
0,609 ^ 0,145 v
1,70 ‰
q
N
B
w
∙ q̅
35,5
500 ∙ 8,851 0,628 % g q
x y
0,2 %
Tz
q
100 ∙ H ∙ D
0,628
100 ∙ 40 ∙ 41 10,31 W
{
→ _^bXdZX cL`Z _`L XE_žL LY L`_YL: 4~∅20 C
T
12,57 W
{
G
Z
∅
4,8 W → D 40,2 W , YLca] L XE YZ` X^`LbadZZ ^`L`]č Z b]^]Z ]dZ bZa] L
Podaci potrebni za crtanje linije zatežu
ć
ih sila
€
6
5
T6
c
5
T6
s ∙ D
196,2
0,947 ∙ 0,41 505,31
€
T6
T
∙ B
w
12,57 ∙ 500 628,5
€
T6
g €
6
Veli
č
ina pomeranja linije:
b 0,75 ∙ 0,41 0,308 ≈ 31 W
Kontrola smi
č
u
ć
ih napona
MB60 → τ
ƒ
1,6 Mpa μ
&'(
0.2%
B500 → σ
,
500,0 MPa br/dpl/d/h 15/10/45/41 cm
Odre
đ
ivanje grani
č
nih uticaja:
q
<
1,6 ∙ g 8 1,8 ∙ p 1,6 ∙ 6,8125 10,9 kN/m′
T
<
1,6 ∙ Tg 8 1,8 ∙ Tp 1,6 ∙ 40,875 65,4 kN/m′
∆
‡
6
C
W
2 8 0.75EG
6
>
0,5
2 8 0.75 ∗ 0,45@ 10,9 6,4
‡
6,ˆ
‡
6
?
∆
‡
6
65,4 ? 6,4 59
τ
(
‡
6,ˆ
b ∙ z
‡
6,ˆ
b ∙ s ∙ D
59
15 ∙ 0,947 ∙ 41 1,013 MPa M τ
ƒ
1,6 MPa
→ smicanje prima samo beton i nije potrebna računska armatura, uzengije se postavljaju konstruktivno
a
<
CzG
μ
&'(
∙ b ∙ e
<
m
0,002 ∙ 15 ∙ 10
2
0,15 cm
{
→ usvojene uzengije: UB∅6/10/20 Ca
<
CzG
0,28 cm
{
G
Dodatna zategnuta podužna armatura:
T
Œ<
1
2 C3τ
ƒ
? τ
(
G ∙ b ∙ z
1
2 C3 ∙ 1,6 ? 1,013G ∙ 0,15 ∙ 0,947 ∙ 0,41 0,1103 MPa
τ
•<,<
m ∙ a
<
CzG
b ∙ e
<
∙ σ
,
Ccosα 8 sinα ∙ ctgθG
2 ∙ 0,28 ∙ 10
•‘
0,15 ∙ 0,10 ∙ 500 ∙ C0 8 1 ∙ 1G 1,866 Mpa
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
9
T
•<,<
z ∙ b ∙ τ
•<,<
0,947 ∙ 0,41 ∙ 0,15 ∙ 1,866 0,109 MN 109 kN
T
&<,<
T
•<,<
8 T
Œ<
109 8 110,3 219,3 kN
∆A
;
”
T
&<,<
2σ
,
Cctg• ? W`
α
G
219,3
2 ∗ 50 Cctg45° ? W` 90°G 2,193 cm
{
A
;,—˜™
Tz
8 ∆A
;
”
10,31
8 2,193 12,503 cm
{
→ YZ`DXEX _^bXdZL cL`Z _`L XE_žL LY L`_YL: 4~∅20 C
T
12,57 W
{
G
T
12,57 W
{
g A
;,—˜™
12,503 cm
{
→ nije potrebno usvajati dodatnu armaturu
Prora
č
un prslina
a
<
0,20 mm
Kontrola se vrši za presek na polovini nosa
č
a.
Usvojena zategnuta armatura:
4~∅20 C
T
12,57 W
{
G
1. Provera neophodnosti prora
č
una prslina
T
š
q
š
g q
›
f
9
L
6
9
30
2~∅20 6,28 W
{
∅ ∙ œ
4 → ∅
2,83 W
L L
•
8 ∅
6
8 ∅ 8
∅
2 2 8 0,6 8 2,0 8
2,0
2
5,6 W
q
›
∅
9
L
6
28,3
30 ∙ 0,2 4,720 %
T
12,57 W
{
š
HD
š
HC7,5 ∙ ∅ 8 LG 15 ∙ C7,5 ∙ 2,83 8 5,6G 402,375 W
{
q
š
T
š
12,57
402,375 0,0312 3,12 % M q′ 4,720 % → _^aXb ]dZ ]^ _dZ
2.Srednje rastojanje prslina
l
—ž
2 ∙ Ca
•
8 0,1 ∙ e
∅
G 8 K
z
∙ K
{
∙
∅
q
š
2 ∙ C2 8 0,1 ∙ 5,8G 8 0,4 ∙ 0,125 ∙
2,83
0,0312 9,70 cm
K
z
0,4 za RA
K
{
0,125 za savijanje
3. Karakteristi
č
na širina prsline
a
¡
1,70
σ
;
E
;
∙ £1 ? β
z
β
{
>
σ
;—
σ
;
@
{
¥ ∙ l
—ž
β
z
1,0 za RA
β
z
0,5 za dugotrajna i više puta ponovljena dejstva

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
11
I
¶¶
b ∙ x
ª
3 8 n ∙ ¿A
;z
∙ Ch ? xG
{
8 A
;{
∙ Cx ? a
{
G
{
À
n
E
;
E
Œ
210
38
5,526
x
n ∙ CA
;z
8 A
;{
G
b
∙ ÁC?1G 8 P1 8
2 ∙ b ∙ Ch ∙ A
;z
8 a
{
∙ A
;{
G
n ∙ CA
;z
8 A
;{
G
{
Â
x
5,526 ∙ C12,57 8 3,14G
15
∙ ÁC?1G 8 P1 8
2 ∙ 15 ∙ C41 ∙ 12,57 8 3,1 ∙ 3,14G
5,526 ∙ C12,57 8 3,14G
{
 14,716 cm
I
¶¶
15 ∙ 14,716
ª
3
8 5,526 ∙ ¿12,57 ∙ C41 ? 14,716G
{
8 3,14 ∙ C14,716 ? 3,1G
{
À 66263,42 cm
‘
E
Œ
I
¸¹
E
Œ
Ã>
14,77
122,625@
ª
∙ 0,001719 ∙ 10
Ä
8 £1 ? >
14,77
122,625@
ª
¥ ∙ 66263,42Å E
Œ
∙ 66448,01
Ugib od stalnog opterećenja u t 0:
v
²,™Ç•
5
384 ∙
g ∙ l
‘
E
Œ
∙ I
¸¹
5
384 ∙
6,8125 ∙ 12
‘
38 ∙ 66448,01 ∙ 10
•{
0,0730 m 7,3 cm
Ugib od ukupnog opterećenja u t 0:
v
²È—,™Ç•
5
384 ∙
Cg 8 pG ∙ l
‘
E
Œ
∙ I
¸¹
5
384 ∙
6,8125 ∙ 12
‘
38 ∙ 66448,01 ∙ 10
•{
0,0728 m 7,28 cm
Ugib od korisnog opterećenja u t 0:
v
—,™Ç•
v
²È—,™Ç•
? v
²,™Ç•
7,28 ? 7,28 0 cm
Ugib od stalnog opterećenja u t ∞:
v
²,™Ç´
v
²,™Ç•
∙ C1 8 λ
™Ç´
G
λ
™Ç´
α
´
2 ? 1,2
A
;{
A
;z
2 ? 1,2
3,14
12,57 1,7 g 0,8
v
²,™Ç´
0,0728 ∙ C1 8 1,7G 0,197 m 19,7 cm
Ugib od korisnog opterećenja u t ∞:
v
—,™Ç´
0 cm
Ë
ÌÍÎ
Ë
Ï,ÐÇ´
8 Ë
Ñ,ÐÇÒ
ÓÔ, Õ ÖÌ
Plan armiranja dat je na crtežu 4.
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
12
Prednaprezanje
Prora
č
un je ra
đ
en pomo
ć
u programa napravljenog u Excel-u.
Zbog malog nagiba od 6% rožnja
č
a je ra
đ
ena kao da je horizontalna, tako da je savijanje oko slabije
ose zanemareno.
Ulazni podaci:
f
bk
=
50
[MPa]
I faza
f
bk
=
60
[MPa]
II faza
σ
u
=
186 [kN/cm
2
]
f
bz,doz
=
3.5
[MPa]
I faza
f
bz,doz
=
2.4
[MPa]
II faza
E
b1
=
32.29766
[GPa]
I faza
E
b2
=
34.0006
[GPa]
II faza
E
u
=
195
[GPa]
E
a
=
210
[GPa]
φ
=
2.8
χ
0.8
ε
sk
=
0.00034
σ
v
=
50 [kN/cm
2
]
Prora
č
un uticaja i napona
ODSTOJANJE TEŽIŠTA KABLOVA OD
DONJEG VLAKNA NOSA
Č
A
z
k
ZATEGNUTA ARMATURA U DONJOJ
ZONI
A
a
NAPONI U GORNJEM I DONJEM
VLAKNU BETONSKOG PRESEKA
σ
g
σ
d
Na po
č
etku zadatka nepoznata je sila prednaprezanja. Dobijanje potrebne sile prednaprezanja se vrši
iterativnim postupkom, gde se unose razli
č
ite vrednosti sile prednaprezanja i ekscentricitet užadi. Sila
koja se dobije ovim iterativnim postupkom treba da zajedno sa ostalim uticajima izaziva napone koji
su u granicama dozvoljenih u karakteristi
č
nim presecima i to u 2 faze koje su merodavne – faza
prednaprezanja i faza eksploatacije. U ovim iteracijama se pretpostavljaju gubici na 5% od ukupne sile
ODSTOJANJE POSMATRANOG
PRESEKA OD PO
Č
ETKA NOSA
Č
A
x
MOMENTI U PRESECIMA
M
TRANSVERZALNE SILE U PRESECIMA
T
NORMALNE SILE U PRESECIMA
N
SILA PREDNAPREZANJA U FAZI
PREDNAPREZANJA JEDNOG UŽETA
N
k0,1
BROJ UŽADI
n

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
14
Tabela 1.
- Presek 1
x=
0
[m]
M=
0
[kNm]
T=
13.875
[kN]
N=
0
[kN]
N
k0,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 2
x=
0.53
[m]
M=
7.029
[kNm]
T=
12.649
[kN]
N=
0
[kN]
N
k0,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 3
x=
1
[m]
M=
12.719
[kNm]
T=
11.563
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 4
x=
1.5
[m]
M=
18.211
[kNm]
T=
10.406
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 5
x=
2
[m]
M=
23.125
[kNm]
T=
9.250
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 6
x=
2.5
[m]
M=
27.461
[kNm]
T=
8.094
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 7
x=
3
[m]
M=
31.219
[kNm]
T=
6.938
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 8
x=
3.5
[m]
M=
34.398
[kNm]
T=
5.781
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 9
x=
4
[m]
M=
37.000
[kNm]
T=
4.625
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 10
x=
4.5
[m]
M=
39.023
[kNm]
T=
3.469
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 11
x=
5
[m]
M=
40.469
[kNm]
T=
2.313
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 12
x=
5.5
[m]
M=
41.336
[kNm]
T=
1.156
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 13
x=
6
[m]
M=
41.625
[kNm]
T=
0.000
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
15
U tabeli 1 su prikazani podaci potrebni za dobijanje vrednosti napona u presecima.
Tabela 2. Naponi u fazi prednaprezanja, pretpostavljeni gubici
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
x=
0.000 0.530 1.000 1.500 2.000 2.500 3.000 3.500 4.000 4.500 5.000 5.500 6.000
σ
g
=
0.000 0.727
-0.92
-0.35 0.150 0.306 0.695 1.023 1.292 1.502 1.651 1.741 1.771
σ
d
=
0.000
-1.11 10.18 9.310 8.531 12.67 12.07 11.57 11.16 10.84 10.61 10.47 10.42
Naponi u fazi prednaprezanja, pretpostavljeni gubici
Tabela 3.
- Presek 1
σ
z
=
NE POSTOJI
ZATEZANJE
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
NE POSTOJI
ZATEZANJE
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 2
σ
z
=
-1.114
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
3.143
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 3
σ
z
=
-0.926
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
3.778
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 4
σ
z
=
-0.359
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
9.763
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 5
σ
z
=
NE POSTOJI
ZATEZANJE
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
NE POSTOJI
ZATEZANJE
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 6
σ
z
=
NE POSTOJI
ZATEZANJE
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
NE POSTOJI
ZATEZANJE
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
-1.114
10.180
9.310
8.531
12.672
12.076
11.573 11.160
10.840 10.611 10.473 10.428
0.727
-0.926
-0.359
0.150 0.306
0.695 1.023
1.292 1.502 1.651 1.741
1.771
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
14.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
17
Stati
č
ki sistem prosta greda, raspona l=12 m
q= 6.8125
[kN/m']
l= 12
[m]
Tabela 4.
- Presek 1
x=
0
[m]
M=
0
[kNm]
T=
40.875
[kN]
N=
0
[kN]
N
k0,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 2
x=
0.53
[m]
M=
20.707
[kNm]
T=
37.264
[kN]
N=
0
[kN]
N
kt,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 3
x=
1
[m]
M=
37.469
[kNm]
T=
34.063
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 4
x=
1.5
[m]
M=
53.648
[kNm]
T=
30.656
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 5
x=
2
[m]
M=
68.125
[kNm]
T=
27.250
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
2
[kom]
z
k
=
0.1
[m]
- Presek 6
x=
2.5
[m]
M=
80.898
[kNm]
T=
23.844
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 7
x=
3
[m]
M=
91.969
[kNm]
T=
20.438
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 8
x=
3.5
[m]
M=
101.336
[kNm]
T=
17.031
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 9
x=
4
[m]
M=
109.000
[kNm]
T=
13.625
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 10
x=
4.5
[m]
M=
114.961
[kNm]
T=
10.219
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 11
x=
5
[m]
M=
119.2188
[kNm]
T=
6.8125
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
- Presek 12
x=
5.5
[m]
M=
121.773
[kNm]
T=
3.406
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
18
- Presek 13
x=
6
[m]
M=
122.625
[kNm]
T=
0.000
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
3
[kom]
z
k
=
0.1167
[m]
U tabeli 4 su prikazani podaci potrebni za dobijanje vrednosti napona u presecima u fazi eksploatacije.
Tabela 5. Naponi u fazi eksploatacije, pretpostavljeni gubici
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
x=
0.000 0.530 1.000 1.500 2.000 2.500 3.000 3.500 4.000 4.500 5.000 5.500 6.000
σ
g
=
0.000 2.141 2.053 3.726 5.223 6.306 7.451 8.420 9.212 9.829 10.26 10.53 10.62
σ
d
=
0.000
-3.28 3.972 1.408
-0.88 1.013
-0.74
-2.22
-3.43
-4.38
-5.05
-5.46
-5.59
Naponi u fazi eksploatacije, pretpostavljeni gubici
Tabela 6.
- Presek 1
σ
z
=
NE POSTOJI
ZATEZANJE
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NE POSTOJI
ZATEZANJE
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 2
σ
z
=
-3.281
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
0.732
POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 3
σ
z
=
NE POSTOJI
ZATEZANJE
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NE POSTOJI
ZATEZANJE
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
-3.281
3.972
1.408
-0.885
1.013
-0.741
-2.225
-3.439
-4.384
-5.058 -5.463 -5.598
2.141 2.053
3.726
5.223
6.306
7.451
8.420
9.212
9.829 10.269
10.533 10.621
-8.000
-6.000
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
20
Tabela 7.
- Presek 1
a) Lom preko armature
A
u
=
0
[cm
2
]
A
a
=
0
[cm
2
]
M
l
=
0
[kNm]
K
l
=
1.810
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
480
[kNm]
K
l
=
1.810
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 2
a) Lom preko armature
A
u
=
0
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
45.2
[kNm]
K
l
=
2.183
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
960
[kNm]
K
l
=
46.361
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 3
a) Lom preko armature
A
u
=
2.8
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
190.14
[kNm]
K
l
=
5.075
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
720
[kNm]
K
l
=
19.216
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 4
a) Lom preko armature
A
u
=
2.8
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
190.14
[kNm]
K
l
=
3.544
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
720
[kNm]
K
l
=
13.421
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 5
a) Lom preko armature
A
u
=
2.8
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
190.14
[kNm]
K
l
=
2.791
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
720
[kNm]
K
l
=
10.569
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 6
a) Lom preko armature
A
u
=
2.8
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
179.5555
[kNm]
K
l
=
2.220
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
8.405
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 7
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.3269
[kNm]
K
l
=
2.754
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
7.393
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 8
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.3269
[kNm]
K
l
=
2.500
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
6.710
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 9
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.3269
[kNm]
K
l
=
2.324
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
6.238
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 10
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.326
[kNm]
K
l
=
2.204
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
5.914
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 11
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.326
[kNm]
K
l
=
2.125
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
5.703
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 12
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.326
[kNm]
K
l
=
2.080
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
5.583
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
21
- Presek 13
a) Lom preko armature
A
u
=
4.2
[cm
2
]
A
a
=
2.26
[cm
2
]
M
l
=
253.326
9
[kNm]
K
l
=
2.066
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
679.92
[kNm]
K
l
=
5.545
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
U tabeli 7 dat je prora
č
un koeficijenta sigurnosti od pojave loma po armaturi i prora
č
un koeficijenta
sigurnosti od pojave loma po betonu. Koeficijent sigurnosti od pojave loma po armaturi je zadovoljen
uz dodavanje armature od 2,26 cm
2
C2~∅12G
u donjoj zoni preseka. Ta dodatna armatura je dovoljna i
za zadovoljenje koeficijenta sigurnosti od pojave prslina u fazi eksploatacije.
Tabela 8.
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
x=
0.000 0.530 1.000 1.500 2.000 2.500 3.000 3.500 4.000 4.500 5.000 5.500 6.000
σ=
-0.76
-0.80
-0.32
-0.14
-0.11
-0.08
-0.07
-0.04
-0.02
-0.01
-0.00
-0.00 0.000
Vrednosti glavnih napona
Pošto je na osnovu prethodno datog prora
č
una dokazano da su u svim presecima normalni naponi u
granicama dozvoljenih, glavni naponi u granicama dozvoljenih, da su koeficijenti sigurnosti od pojave
prslina, koeficijenti sigurnosti od pojave loma po armaturi i koeficijenti sigurnosti od pojave loma po
-0.766
-0.804
-0.184
-0.149
-0.118
-0.060 -0.048
-0.033 -0.021 -0.012
-0.005 -0.001 0.000
-0.900
-0.800
-0.700
-0.600
-0.500
-0.400
-0.300
-0.200
-0.100
0.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
23
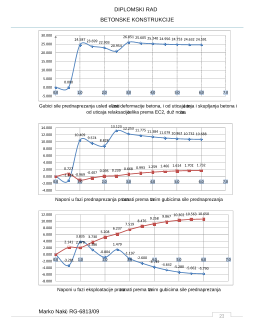
Gubici sile prednaprezanja usled elasti
č
ne deformacije betona, i od uticaja te
č
enja i skupljanja betona i
od uticaja relaksacije
č
elika prema EC2, duž nosa
č
a.
Naponi u fazi prednaprezanja prora
č
unati prema ta
č
nim gubicima sile prednaprezanja
Naponi u fazi eksploatacije prora
č
unati prema ta
č
nim gubicima sile prednaprezanja
0.000
24.587 23.699
22.903
20.954
26.051 25.605 25.240 24.956 24.753 24.632 24.591
-5.000
0.000
5.000
10.000
15.000
20.000
25.000
30.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
-1.114
10.409
9.574
8.828
13.123
12.253 11.775
11.384 11.079 10.862 10.732 10.688
0.727
-0.969
-0.407
0.095 0.239
0.668 0.993
1.259 1.466 1.614 1.702 1.732
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
14.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
-3.281
3.835
1.386
-0.804
1.479
-1.197
-2.600
-3.749
-4.642
-5.280 -5.662 -5.790
2.141 2.078
3.730
5.208
6.237
7.519
8.476
9.258
9.867 10.302
10.563 10.650
-8.000
-6.000
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
24
- Upore
đ
enje rezultata
Naponi prema pretpostavljenim gubicima u fazi eksploatacije
Naponi prema ta
č
nim gubicima u fazi eksploatacije
Planovi armiranja prethodno napregnutog sekundarnog nosa
č
a T45 dati su na crtežima 5,6,7.
-3.281
3.972
1.408
-0.885
1.013
-0.741
-2.225
-3.439
-4.384
-5.058 -5.463 -5.598
2.141 2.053
3.726
5.223
6.306
7.451
8.420
9.212
9.829 10.269
10.533 10.621
-8.000
-6.000
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
-3.281
3.835
1.386
-0.804
1.479
-1.197
-2.600
-3.749
-4.642
-5.280 -5.662 -5.790
2.141 2.078
3.730
5.208
6.237
7.519
8.476
9.258
9.867 10.302 10.563 10.650
-8.000
-6.000
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
26
Dimenzionisanje
MB60 → fb 35,5 Mpa μ
&'(
0.2%
B500 → σ
,
500,0 MPa br/dpl/d/h 15/30/120/110 cm
Odre
đ
ivanje grani
č
nih uticaja:
5
6
1.65
7
8 1.85
9
1,6 ∙ 966,8 1546,88
6
0
M
;<
M
<
8 N
<
>
d
2 ? a@ 1546,88 kNm
B
9
5
6
CD ?
E
9F
2 GHE
9F
1546,88
I1,10 ? 1,20
2 J ∙ 0,5 ∙ 0,3
20,625 5KL M N
35,5 5KL
ε
9
2,0 O1 ? P1 ?
B
9
N Q 2,0 O1 ?
P1 ?
20,625
35,5 Q 0,705 ‰
S
1
1 8
ε
T
ε
9
UD ?
E
9F
2 V 8
E
9F
2
1
1 8 10,0
0,705
>110 ?
30
2 @ 8
30
2
21,26 W M E
9F
30 W
⇒
X YZč] YZ^Z _ ^`L`]č X ^ ]^a_ YLE] LX YLbX_ LX],
E] Zc]dL H/E/D/50/120/110 W
D
e 5
T6
H ∙ N
f
1,10
e 1546,88
0,50 ∙ 35500
3,726 g 1.713
⇒
presek je jednostruko armiran
O
č
itano iz tabele:
3,691 → q̅ 7,714 % s
0,951 t 0,362 u
0,575 ^ 0,134 v
1,525 ‰
q
N
B
w
∙ q̅
35,5
500 ∙ 7,714 0,548 % g q
x y
0,2 %
Tz
q
100 ∙ H ∙ D
0,548
100 ∙ 50 ∙ 110 30,14 W
{
→ _^bXdZX cL`Z _`L XE_žL LY L`_YL: 8~∅25 C
T
39,19 W
{
G
L
z
9,1 W → D 110,9 W , YLca] L XE YZ` X^`LbadZZ ^`L`]č Z b]^]Z ]dZ bZa] L
Podaci potrebni za crtanje linije zatežu
ć
ih sila
€
6
5
T6
c
5
T6
s ∙ D
1546,88
0,951 ∙ 1,10 1478,71
€
T6
T
∙ B
w
39,27 ∙ 500 1963,5
€
T6
g €
6
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
27
Veli
č
ina pomeranja linije:
b 0,75 ∙ 1,10 0,825 ≈ 82 W
Kontrola smi
č
u
ć
ih napona
MB60 → τ
ƒ
1,6 Mpa μ
&'(
0.2%
B500 → σ
,
500,0 MPa br/dpl/d/h 15/30/120/110 cm
Odre
đ
ivanje grani
č
nih uticaja:
q
<
1,6 ∙ g 8 1,8 ∙ p 1,6 ∙ 34,375 55 kN/m′
T
<
1,6 ∙ Tg 8 1,8 ∙ Tp 1,6 ∙ 257,8 412,48 kN
∆
‡
6
C
W
2 8 0.75EG
6
>
0,5
2 8 0.75 ∗ 1,20@ 55 63,25
‡
6,ˆ
‡
6
?
∆
‡
6
412,48 ? 63,25 349,23
τ
(
‡
6,ˆ
b ∙ z
‡
6,ˆ
b ∙ s ∙ D
349,23
15 ∙ 0,951 ∙ 110 2,22 MPa
τ
ƒ
1,6 MPa M τ
(
2,22 MPa M 3 ∙ τ
ƒ
4,8 MPa
→ deo smicanja prima beton a deo računska armatura
T
Œ<
1
2 C3τ
ƒ
? τ
(
G ∙ b ∙ z
1
2 C3 ∙ 1,6 ? 2,22G ∙ 0,15 ∙ 0,951 ∙ 1,10 201,98 kN
T
•<
‡
6,ˆ
? T
Œ<
349,23 ? 201,98 147,25 kN
τ
•<,<
‡
6,ˆ
H ∙ c
147,25
0,15 ∙ 0,951 ∙ 1,10 0,938 5KL
a
<
CzG
τ
•<,<
∙ b ∙ e
<
m ∙ σ
,
Ccosα 8 sinα ∙ ctgθG
0,0938 ∙ 15 ∙ 10
2 ∙ 50 ∙ C0 8 1 ∙ 1G 0,141 cm
{
→ usvojene uzengije: UB∅6/10/20 Ca
<
CzG
0,283 cm
{
G
Dodatna zategnuta podužna armatura:
τ
•<,<
m ∙ a
<
CzG
b ∙ e
<
∙ σ
,
Ccosα 8 sinα ∙ ctgθG
2 ∙ 0,283 ∙ 10
•‘
0,15 ∙ 0,10 ∙ 500 ∙ C0 8 1 ∙ 1G 1,186 Mpa
T
•<,<
z ∙ b ∙ τ
•<,<
0,951 ∙ 1,10 ∙ 0,15 ∙ 1,186 0,186 MN 186,1 kN
T
&<,<
T
•<,<
8 T
Œ<
186,1 8 201,98 388,08 kN
∆A
;
”
T
&<,<
2σ
,
Cctg• ? W`
α
G
388,08
2 ∙ 50 Cctg45° ? W` 90°G 3,88 cm
{
A
;,—˜™
Tz
8 ∆A
;
”
30,14
8 3,88 34,02 cm
{
→ YZ`DXEX _^bXdZL cL`Z _`L XE_žL LY L`_YL: 8~∅25 C
T
39,27 W
{
G
T
39,27 W
{
g A
;,—˜™
34,02 cm
{
→ usvojeno: 8~∅25 C
T
39,27 W
{
G
Prora
č
un prslina
a
<
0,20 mm
Kontrola se vrši za presek na polovini nosa
č
a.
Usvojena zategnuta armatura:
8~∅25 C
T
39,27 W
{
G

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
29
x
n ∙ CA
;z
8 A
;{
G
b
∙ ÁC?1G 8 P1 8
2 ∙ b ∙ Ch ∙ A
;z
8 a
{
∙ A
;{
G
n ∙ CA
;z
8 A
;{
G
{
Â
x
5,526 ∙ C39,27 8 4,52G
15
∙ ÁC?1G 8 P1 8
2 ∙ 15 ∙ C110 ∙ 39,27 8 3,2 ∙ 4,52G
5,526 ∙ C39,27 8 4,52G
{
 42,63 cm
I
¶¶
15 ∙ 42,63
ª
3
8 5,526 ∙ ¿39,27 ∙ C110 ? 42,63G
{
8 4,52 ∙ C42,63 ? 3,2G
{
À 1411276,42 cm
‘
E
Œ
I
¸¹
E
Œ
Ã>
105,08
1546,88@
ª
∙ 3581600 8 £1 ? >
105,08
1546,88@
ª
¥ ∙ 1411276,42Å E
Œ
∙ 1411956,74
Ugib od stalnog opterećenja u t 0:
v
²,™Ç•
5
384 ∙
g ∙ l
‘
E
Œ
∙ I
¸¹
5
384 ∙
34,375 ∙ 15
‘
38 ∙ 1411956,74 ∙ 10
•{
0,0422 m 4,22 cm
Ugib od ukupnog opterećenja u t 0:
v
²È—,™Ç•
5
384 ∙
Cg 8 pG ∙ l
‘
E
Œ
∙ I
¸¹
5
384 ∙
34,375 ∙ 15
‘
38 ∙ 1411956,74 ∙ 10
•{
0,0422 m 4,22 cm
Ugib od korisnog opterećenja u t 0:
v
—,™Ç•
v
²È—,™Ç•
? v
²,™Ç•
4,22 ? 4,22 0 cm
Ugib od stalnog opterećenja u t ∞:
v
²,™Ç´
v
²,™Ç•
∙ C1 8 λ
™Ç´
G
λ
™Ç´
α
´
2 ? 1,2
A
;{
A
;z
2 ? 1,2
4,52
39,27 1,862 g 0,8
v
²,™Ç´
0,0422 ∙ C1 8 1,862G 0,121 m 12,1 cm
Ugib od korisnog opterećenja u t ∞:
v
—,™Ç´
0 cm
Ë
ÌÍÎ
Ë
Ï,ÐÇ´
8 Ë
Ñ,ÐÇÒ
Óñ, Ó ÖÌ
Plan armiranja dat je na crtežu 8.
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
30
Prednaprezanje
Prora
č
un je ra
đ
en pomo
ć
u programa napravljenog u Excel-u.
Zbog malog nagiba od 6% glavni nosa
č
je ra
đ
en kao da je horizontalan.
Ulazni podaci:
f
bk
=
50
[MPa]
I faza
f
bk
=
60
[MPa]
II faza
σ
u
=
186 [kN/cm
2
]
f
bz
=
3.5
[MPa]
I faza
f
bz
=
2.4
[MPa]
II faza
E
b1
=
32.29766
[GPa]
I faza
E
b2
=
34.0006
[GPa]
II faza
E
u
=
195
[GPa]
E
a
=
210
[GPa]
φ
=
2.8
χ
0.8
ε
sk
=
0.00034
σ
v
=
50 [kN/cm
2
]
Prora
č
un uticaja i napona
ODSTOJANJE TEŽIŠTA KABLOVA OD
DONJEG VLAKNA NOSA
Č
A
z
k
ZATEGNUTA ARMATURA U DONJOJ
ZONI
A
a
NAPONI U GORNJEM I DONJEM
VLAKNU BETONSKOG PRESEKA
σ
g
σ
d
ODSTOJANJE POSMATRANOG
PRESEKA OD PO
Č
ETKA NOSA
Č
A
x
MOMENTI U PRESECIMA
M
TRANSVERZALNE SILE U PRESECIMA
T
NORMALNE SILE U PRESECIMA
N
SILA PREDNAPREZANJA U FAZI
PREDNAPREZANJA JEDNOG UŽETA
N
k0,1
BROJ UŽADI
n

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
32
Tabela 11.
- Presek 1
x=
0
[m]
M=
0
[kNm]
T=
53.4375
[kN]
N=
0
[kN]
N
k0,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 2
x=
0.5
[m]
M=
25.828
[kNm]
T=
49.875
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 3
x=
1
[m]
M=
49.875
[kNm]
T=
46.313
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 4
x=
1.5
[m]
M=
72.141
[kNm]
T=
42.750
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 5
x=
2
[m]
M=
92.625
[kNm]
T=
39.188
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 6
x=
2.5
[m]
M=
111.328
[kNm]
T=
35.625
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
6
[kom]
z
k
=
0.15
[m]
- Presek 7
x=
3
[m]
M=
128.250
[kNm]
T=
32.063
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
6
[kom]
z
k
=
0.15
[m]
- Presek 8
x=
3.5
[m]
M=
143.391
[kNm]
T=
28.500
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 9
x=
4
[m]
M=
156.750
[kNm]
T=
24.938
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 10
x=
4.5
[m]
M=
168.328
[kNm]
T=
21.375
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 11
x=
5
[m]
M=
178.125
[kNm]
T=
17.813
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 12
x=
5.5
[m]
M=
186.141
[kNm]
T=
14.250
[kN]
N=
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 13
x=
6
[m]
M=
192.375
[kNm]
T=
10.688
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 14
x=
6.5
[m]
M=
196.828
[kNm]
T=
7.125
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 15
x=
7
[m]
M=
199.500
[kNm]
T=
3.563
[kN]
N=
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 16
x=
7.5
[m]
M=
200.390
[kNm]
T=
0
[kN]
N=
0
[kN]
N
k0,1
=
160
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
U tabeli 11 prikazani su podaci potrebni za dobijanje vrednosti napona u presecima.
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
33
Tabela 12.
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
x=
0.00
0.500
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
σ
g
=
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
σ
d
=
0.00
-2.41
-2.12
-1.85
-1.60
-2.45
-2.24
-2.94
-2.78
-2.64
-2.52
-2.42
-2.34
-2.29
-2.26
-2.25
Naponi u fazi prednaprezanja, pretpostavljeni gubici
Tabela 13.
- Presek 1
σ
z
=
NEMA
σ
z
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
NEMA
σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 2
σ
z
=
-2.413
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.450
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 3
σ
z
=
-2.122
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.650
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 4
σ
z
=
-1.852
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.890
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 5
σ
z
=
-1.603
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
2.183
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 6
σ
z
=
-2.449
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.429
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 7
σ
z
=
-2.244
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.560
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
- Presek 8
σ
z
=
-2.938
[MPa]
σ
z,doz
=
-3.500
[MPa]
K
pr
=
1.191
NE POSTOJI OPASNOST
OD POJAVE PRSLINA
10.46 9.95
9.47
9.03
13.63 13.27
17.59 17.31 17.06 16.85 16.68 16.55 16.45 16.39 16.38
-2.41 -2.12 -1.85
-1.60
-2.45 -2.24 -2.94 -2.78 -2.64 -2.52 -2.42 -2.34 -2.29 -2.26 -2.25
-5.00
0.00
5.00
10.00
15.00
20.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
35
Tabela 14.
- Presek 1
x=
0
[m]
M=
0
[kNm]
T=
257.812
[kN]
N=
0
[kN]
N
kt,1
=
0
[kN]
n=
0
[kom]
z
k
=
0
[m]
- Presek 2
x=
0.5
[m]
M=
124.609
[kNm]
T=
240.625
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 3
x=
1
[m]
M=
240.625
[kNm]
T=
223.437
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 4
x=
1.5
[m]
M=
348.046
[kNm]
T=
206.25
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 5
x=
2
[m]
M=
446.875
[kNm]
T=
189.062
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
4
[kom]
z
k
=
0.125
[m]
- Presek 6
x=
2.5
[m]
M=
537.109
[kNm]
T=
171.875
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
6
[kom]
z
k
=
0.15
[m]
- Presek 7
x=
3
[m]
M=
618.75
[kNm]
T=
154.687
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
6
[kom]
z
k
=
0.15
[m]
- Presek 8
x=
3.5
[m]
M=
691.796
[kNm]
T=
137.5
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 9
x=
4
[m]
M=
756.25
[kNm]
T=
120.312
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 10
x=
4.5
[m]
M=
812.1094
[kNm]
T=
103.125
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 11
x=
5
[m]
M=
859.375
[kNm]
T=
85.9375
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 12
x=
5.5
[m]
M=
898.046
[kNm]
T=
68.75
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 13
x=
6
[m]
M=
928.125
[kNm]
T=
51.5625
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 14
x=
6.5
[m]
M=
949.6094
[kNm]
T=
34.375
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 15
x=
7
[m]
M=
962.5
[kNm]
T=
17.1875
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
- Presek 16
x=
7.5
[m]
M=
966.7968
[kNm]
T=
0
[kN]
N=
0
[kN]
N
kt,1
=
130
[kN]
n=
8
[kom]
z
k
=
0.175
[m]
U tabeli 14 su prikazani podaci potrebni za dobijanje vrednosti napona u presecima u fazi
eksploatacije.
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
36
Tabela 15.
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
x=
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
σ
g
=
0.00
-0.70
0.70
2.00
3.20
3.43
4.42
4.59
5.37
6.05
6.62
7.09
7.45
7.71
7.87
7.92
σ
d
=
0.00
6.28
3.80
1.51
-0.61
1.52
-0.22
1.99
0.62
-0.58
-1.59
-2.42
-3.06
-3.52
-3.79
-3.89
Naponi u fazi eksploatacije, pretpostavljeni gubici
Tabela 16.
- Presek 1
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 2
σ
z
=
-0.704
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
3.407
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 3
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 4
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 5
σ
z
=
-0.606
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
3.962
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 6
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 7
σ
z
=
-0.223
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
10.762
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 8
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
- Presek 9
σ
z
=
NEMA σ
z
[MPa]
σ
z,doz
=
-2.400
[MPa]
K
pr
=
NEMA σ
z
NE POSTOJI OPASNOST OD
POJAVE PRSLINA
6.28
3.80
1.51
-0.61
1.52
-0.22
1.99
0.62
-0.58
-1.59
-2.42
-3.06 -3.52 -3.79 -3.89
-0.70
0.70
2.00
3.20
3.43
4.42
4.59
5.37
6.05
6.62
7.09
7.45
7.71
7.87
7.92
-6.00
-4.00
-2.00
0.00
2.00
4.00
6.00
8.00
10.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
38
- Presek 5
a) Lom preko armature
A
u
=
5.6
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
1253.93
[kNm]
K
l
=
2.806
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
8325
[kNm]
K
l
=
18.629
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 6
a) Lom preko armature
A
u
=
8.4
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
1688.76
[kNm]
K
l
=
3.144
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
8100
[kNm]
K
l
=
15.081
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 7
a) Lom preko armature
A
u
=
8.4
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
1688.76
[kNm]
K
l
=
2.729
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
8100
[kNm]
K
l
=
13.091
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 8
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
3.032
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
11.383
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 9
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.774
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
10.413
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 10
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.583
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
9.697
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 11
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.441
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
9.164
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 12
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.336
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
8.769
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
39
- Presek 13
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.260
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
8.485
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 14
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.209
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
8.293
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 15
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.179
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
8.182
NE POSTOJI OPASNOST
OD POJAVE LOMA PO
BETONU
- Presek 16
a) Lom preko armature
A
u
=
11.2
[cm
2
]
A
a
=
6.28
[cm
2
]
M
l
=
2097.55
[kNm]
K
l
=
2.170
NE POSTOJI OPASNOST OD
POJAVE LOMA PO
ARMATURI
b) Lom preko betona
M
l
=
7875
[kNm]
K
l
=
8.145
NE POSTOJI OPASNOST OD
POJAVE LOMA PO BETONU
U tabeli 17 dat je prora
č
un koeficijenta sigurnosti od pojave loma po armaturi i prora
č
un koeficijenta
sigurnosti od pojave loma po betonu. Koeficijent sigurnosti od pojave loma po armaturi je zadovoljen
uz dodavanje armature od 6,28 cm
2
C2~∅20G
u donjoj zoni preseka. Ta dodatna armatura je dovoljna i
za zadovoljenje koeficijenta sigurnosti od pojave prslina u fazi eksploatacije.
Tabela 18.
presek
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
11.0
12.0
13.0
14.0
15.0
16.0
x=
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
σ=
-2.11
-1.28
-1.15
-1.02
-0.89
-0.63
-0.53
-0.36
-0.28
-0.21
-0.15
-0.10
-0.05
-0.02
-0.01
0.00
Glavni naponi
Pošto je na osnovu prethodno datog prora
č
una dokazano da su u svim presecima normalni naponi u
granicama dozvoljenih, glavni naponi u granicama dozvoljenih, da su koeficijenti sigurnosti od pojave
prslina, koeficijenti sigurnosti od pojave loma po armaturi i koeficijenti sigurnosti od pojave loma po
betonu zadovoljeni, mogao bi se kona
č
no usvojiti presek. Ali kako smo pretpostavili gubitke prora
č
un
ć
e biti, sada kada je poznata sila prednaprezanja, ura
đ
en prema ta
č
nim gubicima.
-2.11
-1.28
-1.15
-1.02
-0.89
-0.63
-0.53
-0.36 -0.28
-0.21 -0.15
-0.10 -0.05 -0.02
-0.01 0.00
-2.50
-2.00
-1.50
-1.00
-0.50
0.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
41
Gubici sile prednaprezanja usled elasti
č
ne deformacije betona, i od uticaja te
č
enja i skupljanja betona i
od uticaja relaksacije
č
elika prema EC2
Naponi u fazi prednaprezanja prora
č
unati prema ta
č
nim gubicima sile prednaprezanja
Naponi u fazi eksploatacije prora
č
unati prema ta
č
nim gubicima sile prednaprezanja
0.00
26.69 26.00 25.37
24.78
29.42 28.98
32.76 32.44 32.16 31.93 31.74 31.59 31.48 31.42 31.39
0.00
5.00
10.00
15.00
20.00
25.00
30.00
35.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
0.00
10.58 10.10 9.64
9.23
13.57 13.24
17.18 16.91 16.69 16.50 16.34 16.22 16.13 16.08 16.06
0.00
-2.44 -2.16 -1.89
-1.65
-2.44 -2.24 -2.84 -2.69 -2.55 -2.44 -2.34 -2.27 -2.22 -2.19 -2.18
-5.00
0.00
5.00
10.00
15.00
20.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
0.00
5.91
3.51
1.29
-0.75
0.52
-1.15
-0.03
-1.34
-2.47
-3.43
-4.22
-4.83 -5.26 -5.52 -5.61
0.00
-0.61
0.77
2.06
3.24
3.66
4.64
5.05
5.81
6.47
7.04
7.50
7.85
8.11
8.26
8.31
-8.00
-6.00
-4.00
-2.00
0.00
2.00
4.00
6.00
8.00
10.00
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
42
Kontrola napona zatezanja
presek
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
x=
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
σ
2
-2.11
-1.282
-1.15
-1.02
-0.89
-0.63
-0.52
-0.35
-0.28
-0.21
-0.14
-0.09
-0.05
-0.02
-0.00
0.00
Glavni naponi zatezanja
B
{,òóš
3,0 5KL cL 5~60 g B
{
2,11 5KL → X`YZHX dZ X^] _YLdZ _cZ ]dL L
L
6
CzG
B
{
∙ H ∙ Z
6
∙ B
T,òó9
2,11 ∙ 0,15 ∙ 0,1
2 ∙ 500
∙ 10
‘
0,316 W
{
_^bXdZX: ~ô∅8/10 CL
6
CzG
0,502 W
{
G
-2.111
-1.282
-1.150
-1.021
-0.895
-0.632
-0.527
-0.359
-0.280
-0.210 -0.148
-0.096 -0.055
-0.024 -0.006
0.000
-2.500
-2.000
-1.500
-1.000
-0.500
0.000
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
44
2.3 PRORA
Č
UN STUBOVA
Odre
đ
ivanje uticaja:
Zadati sistem
Stati
č
ka šema
Sistem je dva puta stati
č
ki neodre
đ
en. Prora
č
un je izvršen metodom sila.
Uslovne jedna
č
ine:
õ
z
ö
zz
8 õ
{
ö
z{
8 ö
z•
0
õ
z
ö
{z
8 õ
{
ö
{{
8 ö
{•
0
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
45
Osnovni sistem
Ekvivalentni sistem
34,375 / ′ ? bZć ^YLč_L`X cL aLb] X^Lč
÷
x,ø,š
∙ ùú
9è
8 ú
9
û ∙ ü
š
∙ ~
x,ø,š
0,20 / ′ cL XEY_čdZ ]šL
ü
š
2,0 cL X^Zć_ X^`Y_ W]d_
~ 6,0 ? Y] LELd_ćL š]Y]L cL ^`_HXbZ XE _`]WLdL bZ`YL

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
47
çêWö
zz
1
3 ∙ 1,0
{
∙ 8,67 8
1
3 ∙ 1,104
{
∙ 9,57 6,778
çêWö
z{
çêWö
{z
1
3 ∙ 1,104
{
∙ 9,57 3,888
çêWö
{{
1
3 ∙ 1,0
{
∙ 8,67 8
1
3 ∙ 1,104
{
∙ 9,57 6,778
- Uticaj stalnog optere
ć
enja
Stalno optere
ć
enje
Mo,g
çêWö
z•
0
çêWö
{•
0
→ õ
z
0, õ
{
0
5
7
5
z
õ
z
8 5
{
õ
{
8 5
ó,7
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
48
‡
7
‡
z
õ
z
8 ‡
{
õ
{
8 ‡
ó,7
7
z
õ
z
8
{
õ
{
8
ó,7

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
50
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
51
Uticaji od seizmike
z
ý
z
/
ý
z
30 ∙ 12 ∙ 0,3 8 8,67 ∙ 12 ∙ 0,3 ∙ 2 8 30 ∙ 12 ∙ 0,2 8 30 ∙ 12 ∙ 0,75 8 3 ∙ 0,16 ∙ 25 ∙ 12 8
8 ∙ 0,1175 ∙ 25 ∙ 12 8 2 ∙ 0,285 ∙ 25 ∙ 15 8 2 ∙ 0,25 ∙ 25 ∙ 8,67 8 0,25 ∙ 25 ∙ 9,57 1320,36
Mo,s
çêWu
zz
þ 5
z
5
z
ê
ê E^
1
3 ∙ 1,0
{
∙ 8,67 8
1
3 ∙ 1,104
{
∙ 9,57 6,778
çêWu
z{
çêWu
{z
þ 5
z
5
{
ê
ê E^
1
3
1
3 ∙ 1,104
{
∙ 9,57 3,888
çêWu
{{
þ 5
{
5
{
ê
ê E^
1
3 ∙ 1,0
{
∙ 8,67 8
1
3 ∙ 1,104
{
∙ 9,57 6,778

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
53
Horizontalno pomeranje vrha objekta od seizmike
çêWö þ 5 ×
z
ê
ê E^
1
3 ∙ 80,50 ∙ 9,57
{
2457,53 → ö
2457,53
177500 0,0138
1,384 W
ö
òóš
600
957
600 1,6 W g ö 1,384 W → _^aXb dZ ]^ _dZ
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
54
Prora
č
un stuba
B
•
0,7 ∙ N
≤
0.35
0,7 ∙ 5~
≤
0.35
516,55
0,5 ∙ 0,5 ∙ 0,7 ∙ 40 ∙ 10
ª
≤
0.35
0,0738
≤
0.35 → _^aXb dZ ]^ _dZ
Klasifikacija konstrukcije prema osetljivosti na horizontalna pomeranja:
∙ P
∑ ý
∑ ç ê
≤
0,20 8 0,10 ∙ ,
≤
3
? _ _ L b]^]L EZNXY LH]aX X ZYad]bX EZaL X^`Y_ W]dZ, ZYZX XE ]bXL
`Z ZadL ]a] XE ]bXL
“
_ adZš`ZdL
”
cL _`]WLdZ ^Z]c ] Z ]a] bZ`YL
? _ _ L HYXd ^ YL`XbL X^`Y_ W]dZ
çH
⋅
êH ? ^_ L Y_`X^`] L ^Lb]dLdZ _ Z]^ Y^ LaX ^`Ld_ ^b]D bZY`] La]D ZaZ ZL`L
cL _ Y_ćZdZ XHdZ `L _ YLbW_ cL Xd] ^Z _`bY
đ
_dZ X^Z`ad]bX^` L X ZYLdL.
X ^Z Y_`X^` ZaZ Z`L ZdL X b]^]], XžZ ^Z _ YXYLč_ _bZ^`]
XE XbLYLd_ćL Y_`X^`
ý ? ^_ L ^b]D bZY`] La]D Z ^ aXL`LW]X]D X `ZYZćZdL, _ ad_č_d_ć] ] EZX
X `ZYZćZdL XdZ Y]DbL`Ld_ ZaZ Z`] cL _ Y_ćZdZ
ý `Zž]L ^Z _ELY]D X^LčL 8 `Zž]L aLb]D X^LčL 8 `Zž]L ^`_HXbL
8 `Zž]L YXbX X Y]bLčL 8 `Zž]L ^Z L 8 `Zž]L ]^`LaLW]dL
ý 1320,36
ç ê
34 ∙
0,5
‘
12 ∙ 3 0,53125 ü
{
9,57
∙ P
∑ ý
∑ ç ê
9,57 ∙ P
1636,75
0,53125 ∙ 10
î
0,531 g 0,20 8 0,10 ∙ 0,20 8 0,10 ∙ 1 0,30
→ X^`Y_ W]dL dZ X ZYad]bL

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
56
Vitkost stuba
- Stub 1
a
]
]
P
ê
P
0,5
‘
12
0,5
{
0,144
10,68
0,144 74,17
25 M
74,17 M 75
→ XHaL^` ^YZEdZ b]` X^`]
- Stub 2
a
]
]
P
ê
P
0,5
‘
12
0,5
{
0,144
10,58
0,144 73,47
25 M
73,47 M 75
→ XHaL^` ^YZEdZ b]` X^`]
- Metoda dopunske ekscentri
č
nosti
Z Z
z
8 Z
•
8 Z 8 Z
258,28
Z
z
5
99,27
258,28 0,384
38,4 W
Z
•
D
300
867
300 2,89 W → Z
•
3 W
Ý ? Û ãÞ ÝàÙ ÝÞã
ãÝã ØÙ Ý ãÝ ÝÞÜ ÝãÛÞ
74,17 g
50
Z
z
E
0,384
0,50
0,769 M 2
7
258,28 g 0.2 ∙
51,66
DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
57
Z
ùZ
z7
8 Z
•
û ∙ >2,718
z• ∙
? 1@
Z
z7
5
7
7
0
258,28 0
u
258,28
153322,69 0,01686
ç ê
œ
{
a
{
0,177083
œ
{
10,68
{
∙ 10
î
15322,69
Z
C0 8 3G ∙ >2,718
•,•zîÄî
z••,•zîÄî∙{,Ä
? 1@ 0,148 W
Z
z
E
0,384
0,50
0,769
Z
E ∙
? 25
100
50 ∙
74,17 ? 25
60
40,975 W
Z 38,4 8 3,0 8 0,148 8 40,975 82,52 W
0,83
5~ 40 → N
25,5 5KL
í 400 500
⁄
? 2 → B
w
400 5KL
H E
⁄
50/50 W
6
1,9 ∙
7
8 2,1 ∙
9
1,9 ∙ 258,28 490,73
6
1,3 ∙
7
8 1,3 ∙
9
8 1,3 ∙
1,3 ∙ 258,286 335,76
6
490,73
5
6
6
∙ Z 490,73 ∙ 0,83 407,30
6
6
H ∙ E ∙ N
490,73
0,50 ∙ 0,50 ∙ 25,5 ∙ 10
ª
0,077
6
5
6
H ∙ E
{
∙ N
407,30
0,50 ∙ 0,50
{
∙ 25,5 ∙ 10
ª
0,128
q̅ 0,24
T
q̅ ∙
N
B
w
∙ H ∙ E 0,24 ∙
25,5
400 ∙ 50 ∙ 50 38,25 W
{
q
x y
50 ? 0.4
74,17
50 ? 0.4 1,083
T,x y
q
x y
100 ∙ H ∙ E
1,083
100 ∙ 50 ∙ 50 27,08 W
{
L, LS
38,25 W
2
→ _^bXdZX: 16í∅18 C
T
40,72 W
{
G

DIPLOMSKI RAD
BETONSKE KONSTRUKCIJE
Marko Naki
ć
RG-6813/09
59
=
∙
∙
=
583,96
0,50 ∙ 0,50 ∙ 25,5 ∙ 10
= 0,183
̅ = 0,34
= ̅ ∙
∙
∙
= 0,34 ∙
25,5
400
∙ 50 ∙ 50 = 54,19
!
=
"
50
− 0.4 =
73,47
50
− 0.4 = 1,069
,
!
=
!
100
∙
∙
=
1,069
100
∙ 50 ∙ 50 = 26,735
&, &'
= 54,19
2
→ )*+,-./,: 161∅22 (
= 60,82
)
Planovi armiranja dati su na cretežima 12,13.
2.4 GRAFI
Č
KI PRILOZI ZA BETONSKE KONSTRUKCIJE




DIPLOMSKI RAD
FUNDIRANJE
Marko Naki
ć
RG-6813/09
71
Dubina
č
ašice
Prema Ulickom
'
č
'
(
) 5
55
Prema Stevanovi
ć
u
*+ #&# ,-& "%* :
/
/
∙ 1 0,15 → '
č
1,2 ∙
/
/
∙ 2 2,00 → '
č
2,0 ∙
/
/
∙
197,32
258,28 ∙ 0,5 1,528 → ,&-%34# + ,$+
'
č
51,2 )
2 6 1,20
2 6 0,15 ∙ 71,528 6 0,1589 ∙ 50 1,796 ∙ 50 89,79
→ !"#$%&+ ",!,&+ č+š, % '
č
100
Odre
đ
ivanje nosivosti tla prema Pravilniku iz 1990. god.
;
<
0,5 ∙ ∙ =
>
∙
?
∙ @
?
∙ ,
?
) 7
A
) ; ∙ tan
A
8
E
∙ @
E
∙
E
∙ ,
E
) ;
21,15
28° → tan
A
tan
1,5
tan 28°
1,5
0,35447 →
A
19,5°
*+
A
19,5° →
?
2,97
E
13,93
A
0
F G
/
) H
I
258,28 ) 2,5
J
∙ 1,65 ∙ 21,15 476,39
F
I
98,05 ) 99,27 ) 1,65 ∙ 726,54 ) 11,318 259,77
DIPLOMSKI RAD
FUNDIRANJE
Marko Naki
ć
RG-6813/09
72
%
K
∑
I
∑ G
259,77
476,39 0,545
=
>
M
>
= 6 2%
K
2,5 6 2 ∙ 0,545 1,409
@
?
1 6 0,4 ∙
=
>
M
>
1 6 0,4 ∙
1,409
1,409 0,60
@
E
1 ) 0,2 ∙
=
>
M
>
1 ) 0,2 ∙
1,409
1,409 1,20
E
1 ) 0,35 ∙
N
O
M
>
1 ) 0,35 ∙
1,65
1,409 1,410
P
A
Q
R
> A
) ∑ G tan
A
37,85
1,409
J
∙ 0 ) 476,39 ∙ 0,35447 0,224
→ ,
?
0,85 ,
E
0,78
; 0,15 ∙ 25 ) 1,5 ∙ 20 33,75
J
;
<
0,5 ∙ 21,15 ∙ 1,409 ∙ 2,97 ∙ 0,6 ∙ 0,85 ) 70 ) 33,75 ∙ 0,354478 ∙ 13,93 ∙ 1,2 ∙ 1,41 ∙ 0,78 ) 33,75
→ ;
<
276,26
J
∑ G
R
>
476,39
1,409
J
239,96
J
1 ;
<
276,26
J
Kontrola pritisaka na tlo
Uticaj od stalnog optere
ć
enja
S
T,J
∑ G
R
476,39
2,5
J
76,22
J
Uticaj od stalnog, povremenog i seizmike
S
T,J
∑ G
R ±
6 ∙ ∑
I
=
476,39
2,5
J
±
6 ∙ 259,77
2,5
76,22 ± 99,75
→ S
T
175,97
J
1 ;
<
276,26
J
→ S
J
623,53
J
1 0
→ - # &% ! % + 43, , *+-%*+&$%, 4#-3%V+& $% 4#&#"+& 43#3+č &
=
2 6 %
K
2,50
2 6 0,545 0,705
=
>
3 ∙
3 ∙ 0,705 2,115
S
A<W
2 ∙ ∑ G
=
>
∙ M
>
2 ∙ 476,39
2,115 ∙ 2,115 213,00
J
1 ;
<
276,26
J

DIPLOMSKI RAD
FUNDIRANJE
Marko Naki
ć
RG-6813/09
74
Podužna armatura u
č
ašici
%
∑
∑
203,00
258,28 0,786
'
1,05
%
0,786 2 0,3 ∙ 1,05 0,315
→ ! č+$ % ! %&-3,č&#h #4-%3%ć%&$+
R
<
R
<
Z
∙ 7% 6 '
) 8
S
e
∙ '
<
413,248 ∙ 7128,6 6 105 ) 29,38
40 ∙ 100
5,46
J
→ !"#$%&# 8f∅10 7R
<
6,28
J
8
Popre
č
na armatura u
č
ašici
R
W
Z
)
Z
∙ '
(
6
Z
∙ j
S
e
∙ ∑ *
W
256,52 ∙ 10
J
) 49,21 ∙ 115 6 413,25 ∙ 25
40 ∙ 423
1,24
J
→ !"#$%&# 4f∅8 7R
<
2,01
J
8
Plan armiranja dat je na cretežu 14.
DIPLOMSKI RAD
FUNDIRANJE
Marko Naki
ć
RG-6813/09
75
Kontrola probijanja
k
>
R
>
S
X l
) S
XT
2S
X l
S
XT
S
X
) S
X
) S
X
41,32 ) 54,93 ) 44,82 141,07
J
S
XJ
S
X
) S
X
) S
X
41,32 6 54,93 6 44,82 658,43
J
S
X l
S
XT
) S
XJ
2
141,07 6 58,43
2
41,32
J
/
6 R
_
∙ S
X l
258,28 6 4 ∙ 41,32 93
R
_
71,1 ) 2 ∙ 0,458 ∙ 71,1 ) 2 ∙ 0,458 4
J
>
93
41,32 ) 141,07
2 ∙ 41,32
205,25
R
m2 ∙ 71,1 ) 0,458 ) 2 ∙ 71,1 ) 0,458n ∙ 0,45 2,79
J
k
205,25
2,79
73,57
J
0,0736 o+
F ^
<
44∅12 44 ∙ 1,13 57,2
J
a
∑ ^
<
R
57,2
2,79 ∙ 10
p
0,00205 → a 0,205 %
T
1,3 ∙ q ∙ ra 1,3 ∙ 1,3 ∙ r0,205 0,765
2
3 ∙
T
∙ k
<
2
3 ∙ 0,765 ∙ 0,8 0,408 o+
k
0,0736 o+ 1
2
3 ∙
T
∙ k
<
0,408 o+ → ",!,&+ -% % $+ # h#"+3+ 4#h % 43#V,$+&$+
3.2 GRAFI
Č
KI PRILOZI ZA FUNDIRANJE

DIPLOMSKI RAD
TEHNOLOGIJA BETONA
Marko Naki
ć
RG-6813/09
77
4. TEHNOLOGIJA BETONA
Izra
č
unati potrebnu koli
č
inu betona za izradu sekundarnih nosa
č
a T45 (dati zaokruženo na 1m
3
).
Na osnovu izra
č
unate koli
č
ine betona u ta
č
ki 1, odrediti potreban broj kontrolnih betonskih tela za
dokazivanje marke betona uzimaju
ć
i u obzir odredbe PBAB 87. Pretpostaviti broj dana betoniranja.
Odrediti kriterijum za dokazivanje marke betona prema odredbama PBAB na osnovu broja kontrolnih
tela iz ta
č
ke 2.
Sra
č
unati recepturu za beton MB60 sa tri frakcije drobljenog agregata. Usvojiti cement klase 52,5R i
te
č
nu konzistenciju (klasa sleganja S4).
Navesti mere za spre
č
avanje prekomernog skupljanja betona.
4.1 PRORA
Č
UN
Potrebna koli
č
ina betona za izradu sekundarnog nosa
č
a T45
ž 1
ž
č
.
= ∗ ∗ = 40 ∗ 12 ∗ 0,1175 = 56,4 ≈ 56
$
Potreban broj kontrolnih tela za dokazivanje marke betona
Uzimaju
ć
i u obzir odredbe PBAB 87 je po jedno kontrolno betonsko telo na 50 m
3
u jednoj partiji
betona, ali ne manje od 3 betonska tela. Dnevno se vrši betoniranje 7 rožnja
č
a, za ukupan broj od 40
rožnja
č
a potrebno je 6 betoniranja. Za svako betoniranje se uzima jedno kontrolno telo. Na osnovu
toga sledi da je potrebno uzeti 6 kontrolnih betonskih tela.
Kriterijum za dokazivanje marke betona
Prema odredbama PBAB 87 kriterijum za dokazivanje marke betona je kriterijum 1.
Kriterijum 1 se primenjuje ako je broj rezultata ispitivanja kontrolnih betonskih tela jedne partije
betona 3 do 15. Prilikom ispitivanja istinitosti kriterijuma u prora
č
un se uzimaju po tri uzastopna
rezultata ispitivanja:
%
&',()
≥ +, +
.
%
&',/01
≥ +, −
3
gde su:
.
=
3
= 3 +5
za uhodanu proizvodnju betona;
%
&',()
– aritmeti
č
ka sredina tri uzastopna rezultata ispitivanja;
%
&',/01
– najmanja vrednost od tri uzastopna rezultata ispitivanja.
DIPLOMSKI RAD
TEHNOLOGIJA BETONA
Marko Naki
ć
RG-6813/09
78
Receptura za beton
izbor vrste materijala za spravljanje betona, pri
č
emu se u obzir uzima vrsta konstrukcije i
agresivnost uticaja okolne sredine na konstrukciju
odre
đ
ivanje veli
č
ine maksimalnog zrna agregata na osnovu sra
č
unavanja efekta zida-efekta
oplate i efekta rešetke
AB sekundarni nosa
č
T45:
Armatura B400/500 i UŽE1620/1860 b/h/b
r
=40/45/15 cm
- I uslov:
Najkrupnije zrno agregata je potrebno da zadovolji slede
ć
e uslove:
6 7
/01
4 , 6 7 1,25 ∗
/01
Posmatran je presek sa najguš
ć
om armaturom, gde su raspore
đ
ene 4B
∅
12 u gornjoj zoni i 4B
∅
16
u donjoj zoni.
/01
= 10 ⇒ 6
/9:
7
10
4 = 2,5
/01
= 4,4 ⇒ 6
/9:
7 1,25 ∗
/01
= 1,25 ∗ 4,4 = 5,5
- II uslov (efekat rešetke):
Agregat koji ima najve
ć
e zrno D
max
ć
e prolaziti
izme
đ
u šipki armature ako je za re
č
ni agregat E
r
<1,4
ili za drobljeni agregat E
r
<1.2.
;
)
=
6
/9:
< = 1,2
> >
< = 2 =
4,4
2 = 2,2
;
)
=
6
/9:
1,5 = 1,2 ⇒ 6
/9:
= 1,2 ∗ 2,2 = 3,3

DIPLOMSKI RAD
TEHNOLOGIJA BETONA
Marko Naki
ć
RG-6813/09
80
Maksimalna dozaža cementa za 1m3 betona ne treba da pre
đ
e 500 kg.
Imaju
ć
i u vidu da se koristi drobljeni agregat onda u 500 kg/m3 ulazi i kameno brašno (filer). Na
osnovu iskustva dozaža cementa se usvaja 460 kg/m3.
Nova koli
č
ina vode je:
H
=
H
∗ N
O
= 460 ∗ 0,376 = 173 >
Sa ovako malom koli
č
inom vode ne može se dobiti beton te
č
ne konzistencije. Zato moramo da
koristimo odgovaraju
ć
i superplastifikator.
Iz tehni
č
kog kataloga lista za Sika ViskoCrete 4000BP usvajamo dozažu od 1,6% od
O
.
(U&.&V9(W.
= 0,016 ∗ 460 = 7,36 >
$
Izra
č
unavanje potrebne koli
č
ine agregata
9
P
(9
+
O
P
(O
+
H
P
(H
+
9X
P
(9X
+
&
= 1
9
2700 +
460
3050 +
173
1000 + 0,02 +
7,36
1080 = 1 ⇒
9
= 1753 >
YZ[
= 0,40 ∗ 1753 = 701,2 ≈ 701 >
[ZS
= 0,20 ∗ 1753 = 350,6 ≈ 351 >
SZ.
= 0,40 ∗ 1753 = 360,05 ≈ 701 >
⇒ = 1753 + 460 + 173 = 2386 >
Mere za spre
č
avanje prekomernog skupljanja betona
Pod skupljanjem betona se podrazumeva smanjenje njegove zapremine koje je vezano za hidrataciju
cementa i gubitak vlage, pri
č
emu ono ne zavisi od spoljašnjeg optere
ć
enja. Imaju
ć
i u vidu da se
kameni agregat može smatrati inertnim u pogledu promene zapremine u toku vremena, dolazi se do
zaklju
č
ka da je skupljanje betona povezano sa skupljanjem cementne paste. Do skupljanja dolazi iz
nekoliko razloga:
I
usled toga što je zapremina produkata hidratacije manja od polazne zapremine sveže cemente
paste – hidrataciono skupljanje,
I
usled isparavanja vode u periodu vezivanja cementa – plasti
č
no skupljanje
I
ulsed isparavanja vode u periodu o
č
vrš
ć
avanja cemente paste, odnosno u peridou posle kraja
vezivanja – hidrauli
č
ko skupljanje
DIPLOMSKI RAD
TEHNOLOGIJA BETONA
Marko Naki
ć
RG-6813/09
81
Takve promene se „prenose“ i na beton. Pri tome treba imatu u vidu da se radi o nehomogenom
materijalu, pa stoga veli
č
ina skupljanja kod betona zavisi i od koli
č
ine i vrste cementa, vodocementnog
faktora, granulometrijskog sastava, vrste agregata,
č
vrsto
ć
e betona, termohigrometrijskih uslova
okoline, brzine vetra, itd.
Plasti
č
no skupljanje u odnosu na ostale vrste skupljanja je najve
ć
e, ali odre
đ
enu olakšavaju
ć
u okolnost
predstavlja to što se dešava u vreme kada je betonska masa još uvek u odre
đ
enoj meri fluidna. Bez
obzira na to, zbog nehomogenosti strukture betona i prisustva armature, efekat plasti
č
nog skupljanja
nije uniforman u betonskoj masi što izaziva pojavu napona zatezanja koji dalje uslovljava nastanak
prslina. Ovakve prsline se naj
č
eš
ć
e manifestuju na horizontalnim površinama betonskih elemenata,
zatim na mestima veze sa drugim elementima, na konturama elemenata, tj. na mestima gde je brzo
isparavanje vlage iz betona mogu
ć
e.
Pojava prslina usled plasti
č
nog skupljanja u praksi je naro
č
ito izražena u uslovima velike brzine vetra,
male relativne vlažnosti i visoke temperature vazduha, kao i visoke temperature betona. Ako prsline
nastanu
č
esto se prostiru od jedne do druge ivice po površini elementa.
Poznato je da se betoni spravljaju sa ve
ć
om koli
č
inom vode nego što je potrebno za hidrataciju
cementa iz razloga postizanja željene konzistencije betona. Višak vode
ć
e nakon o
č
vrš
ć
avanja betona
sporije ili brže isparavati usled
č
ega nastaje tzv. hidrauli
č
ko skupljanje koje je tako
đ
e uzrok nastanka
napona u betonu. U uslovima spre
č
enog hidrauli
č
kog skupljanja može do
ć
i do nastanka prslina ili
vitoperenja elemenata betonske konstrukcije. Iz tih razloga, na primer kod plo
č
a, treba predvideti
dilatacione razdelnice kako bi se predupredila pojava nasumi
č
nih prslina i kako bi se eventualno
ograni
č
ile na željenu lokaciju gde bi se pojavile u formi koja se lako može ispuniti adekvatnim
zaptivnim (reparaturnim) materijalom.
U praksi je hidrauli
č
ko skupljanje mnogo zna
č
ajnije nego ranije opisano plasti
č
no skupljanje. Faktori
koji uti
č
u na veli
č
inu hidrauli
č
kog skupljanja su veoma brojni i mogu se podeliti na one koji se ti
č
u
karakteristika cemente paste, zatim samog betona, kao i uslova sredine.
Kada se radi o cementnoj pasti zna
č
ajniji su vodocementni faktor, stepen hidratacije, vrsta cementa,
sadržaj vlage, prisustvo aditiva i temperatura na kojoj o
č
vrš
ć
ava. Sastav cementa može uticati na
skupljanje cementne paste i betona, ali se smatra da uticaj nije veliki, kao i da ta
č
ne relacije izme
đ
u
sastava cementa i skupljanja nisu još uvek dovoljno prou
č
ene. Generalno je prihva
ć
en stav da je
skupljanje ve
ć
e ako se za spravljanje betona koriste cementi sa dodacima, naro
č
ito ako imaju ve
ć
u
fino
ć
u mliva. Ve
ć
e dozaže cementa doprinose ve
ć
em skupljanju, naro
č
ito ako se radi o dozažama
ve
ć
im od 400 kg/m
3
betona. Betoni koji se spravljaju sa ve
ć
im vodocementnim faktorom imaju ve
ć
e
hidrauli
č
ko skupljanje što se dovodi u vezu sa njihovom kapilarnom poroznoš
ć
u.
Kada je re
č
o betonu od zna
č
aja je i koli
č
ina agregata u betonu, debljina betonskog elemnta, odnos
površine i zapremine betonskog elementa. Ve
ć
a koli
č
ina agregata u betonu doprinosi manjem
skupljanju, a naro
č
ito kada je granulometrijski sastav takav da omogu
ć
ava dobro kompatktiranje
betona prilikom ugradnje. Skupljanje je više izraženo kod tankih betonskih elemenata što se dovodi u
vezu sa lakšim isušivanjem u odnosu na betonske elemente ve
ć
ih popre
č
nih preseka.
Parametri koji se ti
č
u sredine odnose se na termohigrometrijske uslove, brzinu isušivanja, kao i vreme
trajanja tog procesa. Poptuno je logi
č
an zaklju
č
ak da
ć
e skupljanje biti ve
ć
e ako je temperatura okoline
i samog betona ve
ć
a, a vlažnost vazduha niža.

DIPLOMSKI RAD
TEHNOLOGIJA BETONA
Marko Naki
ć
RG-6813/09
83
Skupljanje (i bubrenje) betona se mogu utvrditi eksperimentalim putem, što je od posebnog interesa
kod zna
č
ajnih konstruktivnih elemenata i objekata. Procedura ispitivanja definisana je standardnom
SRPS U.M1.029:1983.
U cilju predupre
đ
enja skupljanja betona mogu se koristiti i ekspazivni cementi
č
iji je najraniji razvoj
po
č
eu u Rusiji i Francuskoj. Radi se o cementima koji sadrže dodatak koji u odre
đ
enoj meri
ekspandira i koji je dobijen pe
č
enjem mešavine sadre, boksita i krede. Ovaj dodatak reaguje sa vodom
i stvara etringit kojem se pripisuje ekspanzija cemente paste. Kao stabilizator koji
ć
e ograni
č
iti
ekspanziju etringita koristi se mlevena granulovana zgura. Za betone koji se prave sa ekspanzivnim
cementom karakteristi
č
no je da tokom negovanja u vlažnoj sredini (obi
č
no prvih sedam dana) bubre, a
kasnije kada su izloženi sušenju skupljaju se u meri koja odgovoara prethodno dostignutom bubrenju.
Tako se u kona
č
nom ishodištu dobija beton koji nije ili je doživeo vrlo male deformacije skupljanja,
znatno manje nego beton sa klasi
č
nim portland cementima.
Još neke mere za spre
č
avanje prekomernog skupljanja betona:
I
Betoniranje u kasnim ve
č
ernjim
č
asovima ili tokom no
ć
i
I
Zaštita izloženih površina odmah po završenoj ugradnji i finalnoj obradi površine betona
I
Nega u uslovima visoke vlažnosti (prekrivanje slobodnih površina betona jutanom tkaninom,
prskanje slobodnih površina betona vodom, nanošenje sredstava koja na površini betona
stvaraju vodonepropusnu prevlaku (tzv. membrane), nanošenje sloja peska koji se održava
vlažnim itd.)
DIPLOMSKI RAD
Marko Naki
ć
RG-6813/09
84
5. ZAKLJU
Č
AK
Na osnovu prethodno izloženog, može se zaklju
č
iti da se dobijaju manje koli
č
ine armature prethodnim
naprezanjem elemenata u odnosu na klasi
č
no armiranje. Tako
đ
e kontrola pojave prslina je bolja
prethodnim naprezanjem. Prora
č
un ugiba nije ura
đ
en ali logi
č
no je da su ugibi manji nego kod
klasi
č
nog armiranja. Sve ovo naravno daje prednost prethodnom naprezanju u odnosu na klasi
č
no
armiranje. Što se ti
č
e samog prora
č
una prethodnim naprezanjem, može se videti da je kod ve
ć
ih sila
prednaprezanja, ve
ć
i i gubitak, tako da se ne može uvek prora
č
un uraditi za pretpostavljene gubitke.
Stubovi i
č
ašice su armirani klasi
č
no i ne postoje neke posebne napomene, osim izloženog na
č
ina
prora
č
una.
Što se ti
č
e tehnologije betona vidi se da za postizanje visokih marki betona nije potrebna neka znatno
ve
ć
a koli
č
ina cementa u odnosu na nešto niže marke betona, ve
ć
je potrebna ispravna receptura, što
podrazumeva smanjenje koli
č
ine vode upotrebom aditiva (u ovom slu
č
aju superplastifikatora).

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti


























![Kvantni prinos prelaza od 521kev iz raspada [196]Au](https://public-cdn.studenti.rs/132292/thumbnails/thumbnail-320.jpg)
































